题目链接
[NOIP2018 提高组] 旅行
题目描述
小 Y 是一个爱好旅行的 OIer。她来到 X 国,打算将各个城市都玩一遍。
小 Y 了解到,X 国的 n n n 个城市之间有 m m m 条双向道路。每条双向道路连接两个城市。 不存在两条连接同一对城市的道路,也不存在一条连接一个城市和它本身的道路。并且, 从任意一个城市出发,通过这些道路都可以到达任意一个其他城市。小 Y 只能通过这些 道路从一个城市前往另一个城市。
小 Y 的旅行方案是这样的:任意选定一个城市作为起点,然后从起点开始,每次可 以选择一条与当前城市相连的道路,走向一个没有去过的城市,或者沿着第一次访问该 城市时经过的道路后退到上一个城市。当小 Y 回到起点时,她可以选择结束这次旅行或 继续旅行。需要注意的是,小 Y 要求在旅行方案中,每个城市都被访问到。
为了让自己的旅行更有意义,小 Y 决定在每到达一个新的城市(包括起点)时,将它的编号记录下来。她知道这样会形成一个长度为 n n n 的序列。她希望这个序列的字典序 最小,你能帮帮她吗? 对于两个长度均为 n n n 的序列 A A A 和 B B B,当且仅当存在一个正整数 x x x,满足以下条件时, 我们说序列 A A A 的字典序小于 B B B。
- 对于任意正整数 1 ≤ i < x 1 ≤ i < x 1≤i<x,序列 A A A 的第 i i i 个元素 A i A_i Ai 和序列 B B B 的第 i i i 个元素 B i B_i Bi 相同。
- 序列 A A A 的第 x x x 个元素的值小于序列 B B B 的第 x x x 个元素的值。
输入格式
输入文件共 m + 1 m + 1 m+1 行。第一行包含两个整数 n , m ( m ≤ n ) n,m(m ≤ n) n,m(m≤n),中间用一个空格分隔。
接下来 m 行,每行包含两个整数 u , v ( 1 ≤ u , v ≤ n ) u,v (1 ≤ u,v ≤ n) u,v(1≤u,v≤n) ,表示编号为 u u u 和 v v v 的城市之 间有一条道路,两个整数之间用一个空格分隔。
输出格式
输出文件包含一行, n n n 个整数,表示字典序最小的序列。相邻两个整数之间用一个 空格分隔。
样例 #1
样例输入 #1
6 5
1 3
2 3
2 5
3 4
4 6
样例输出 #1
1 3 2 5 4 6
样例 #2
样例输入 #2
6 6
1 3
2 3
2 5
3 4
4 5
4 6
样例输出 #2
1 3 2 4 5 6
提示
【数据规模与约定】
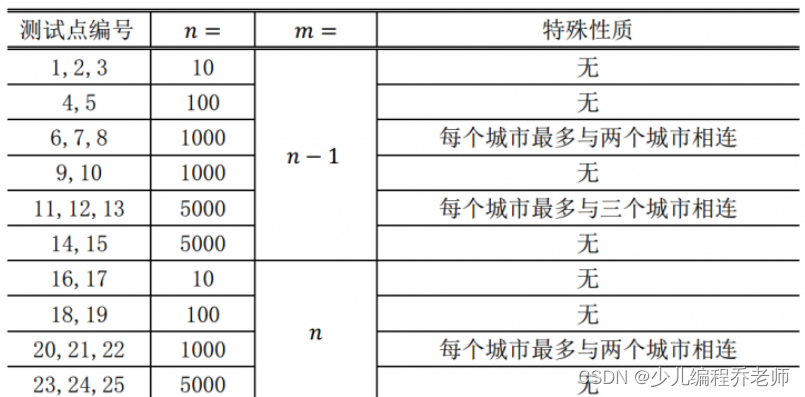
对于 100 % 100\% 100% 的数据和所有样例, 1 ≤ n ≤ 5000 1\le n \le 5000 1≤n≤5000 且 m = n − 1 m = n − 1 m=n−1 或 m = n m = n m=n 。
对于不同的测试点, 我们约定数据的规模如下:
算法思想
根据题目描述:
- 任意选定一个城市作为起点,然后从起点开始,每次可以选择一条与当前城市相连的道路,走向一个没有去过的城市,或者沿着第一次访问该 城市时经过的道路后退到上一个城市
- 在旅行方案中,每个城市都被访问到
访问过程的就是一个DFS序列,要求的其中字典序最小的序列。
从数据范围来看,有 m = n − 1 m = n − 1 m=n−1 或 m = n m = n m=n两种情况,由于从任意一个城市出发,通过这些道路都可以到达任意一个其他城市,也就是说:
- 当 m = n − 1 m = n − 1 m=n−1 时,城市与道路构成一棵树
- 当 m = n m = n m=n时,就是在树上在加一条边,构成基环树,也叫环套树,是一种有 n n n个点 n n n条边的图。
树的深度优先遍历
先处理 m = n − 1 m = n - 1 m=n−1的情况,即对一棵树进行DFS。为了得到字典序最小的DFS序列,就必须从 1 1 1号点开始遍历,每次按编号从小到大的顺序遍历所有子节点。
时间复杂度
DFS遍历树的时间复杂度为 O ( n + m ) O(n+m) O(n+m)。
代码实现(60分)
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 5005;
vector<int> g[N];
vector<int> ans(N, N); //答案序列全部初始化为N
int cnt = 0;
bool st[N];
int n, m;
void dfs(int u)
{
st[u] = 1;
ans[cnt ++] = u;
for(int v : g[u]) //遍历子结点
{
if(st[v]) continue;
dfs(v);
}
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 0; i < m; i ++)
{
int a, b;
scanf("%d%d", &a, &b);
g[a].push_back(b), g[b].push_back(a); //连接a和b的双向边
}
//对每个节点的子节点按编号从小到大排序
for(int i = 1; i <= n; i ++) sort(g[i].begin(), g[i].end());
dfs(1);
for(int i = 0; i < n; i ++) cout << ans[i] << " ";
return 0;
}
基环树
在上述实现中,只会遍历 n n n个点和与其相邻的的 n − 1 n−1 n−1条边。当 m = n m = n m=n时,就是在树上在加一条边,即树中有一个环,构成基环树。那是否要先把环找出来再处理呢?
从数据范围来看, 1 ≤ n ≤ 5000 1\le n \le 5000 1≤n≤5000 , n n n比较小,可以枚举一条构成环的边,将其删除;然后DFS求出最小字典序即可。
在DFS过程中,通过维护当前序列和最优序列的大小关系可以进行最优性剪枝。如果当前序列的字典序一定大于最优序列,则直接退出。
时间复杂度
- 枚举边的时间复杂度为 O ( m ) O(m) O(m)
- DFS遍历树的时间复杂度为 O ( n + m ) O(n + m) O(n+m)
总的时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
代码实现(100分)
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 5005;
vector<int> g[N];
vector<int> ans(N, N); //答案序列,全部初始化为N
vector<int> cur(N); //存储当前搜索序列
int cnt, cmp;
bool st[N];
int n, m, du, dv;
vector<PII> e;
void dfs(int u)
{
if(cmp == 0) //当前序列和答案序列相等
{
if(u < ans[cnt]) cmp = -1; //当前序列字典序更小,继续搜索
if(u > ans[cnt]) { cmp = 1; return ; } //当前序列字典序更大,剪枝
}
st[u] = 1; //标记已访问
cur[cnt ++] = u; //存储访问的城市编号
for(int v : g[u]) //遍历子结点
{
if(st[v] || (u == du && v == dv) || (u == dv && v == du)) continue;
dfs(v);
}
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 0; i < m; i ++)
{
int a, b;
scanf("%d%d", &a, &b);
g[a].push_back(b), g[b].push_back(a); //连接a和b的双向边
e.push_back({a, b}); //存边
}
//对每个节点的子节点按编号从小到大排序
for(int i = 1; i <= n; i ++) sort(g[i].begin(), g[i].end());
if(m == n - 1)
{
dfs(1);
ans = cur;
}
else
{
for(int i = 0; i < m; i ++) //枚举要删除的边
{
du = e[i].first, dv = e[i].second;
//cmp用来比较搜索序列和答案序列的字典序,初始为0表示相等
cnt = cmp = 0;
memset(st, 0, sizeof st);
dfs(1);
if(cnt == n && cmp < 0) //遍历完所有的点,并且搜索序列的字典序更小
ans = cur;
}
}
for(int i = 0; i < n; i ++) cout << ans[i] << " ";
return 0;
}