一、归并排序的背景

1. 分治算法

归并排序，本质上就是分治算法的一种，那么什么是分治算法呢。在算法与程序设计中，我们采用分而治之的策略就是分治算法，其核心就是把一个大规模的问题分解为若干小规模的相同子问题，分而治之，从而达到减少时间复杂度，提高运算效率的目的。

2. 分治算法的解题步骤

2.1 分解

把要解决的问题分解成若干个规模较小的、相互独立的、与原问题形式相同的子问题。

2.2 治理

寻求若干个子问题的解决办法，只要我们把子问题划分的足够小，我们就可以用简单的方法解决问题。

2.3 合并

按照原问题的要求，将子问题逐层分解操作之后，再次合并构成原问题的解。

2. 归并排序

2.1 大致思路

1. 把待排序的数组中的元素分成大小一致的两个子序列。
2. 对两个子序列进行排序。
3. 将排好序的两个子序列进行合并，得到最终的序列。
4. 如此往复分解，直至最后的子序列中只含有一个元素为止。

2.2 算法分析

以数组【1, 3, 5, 1, 6, 100, 985, 221】为例子。

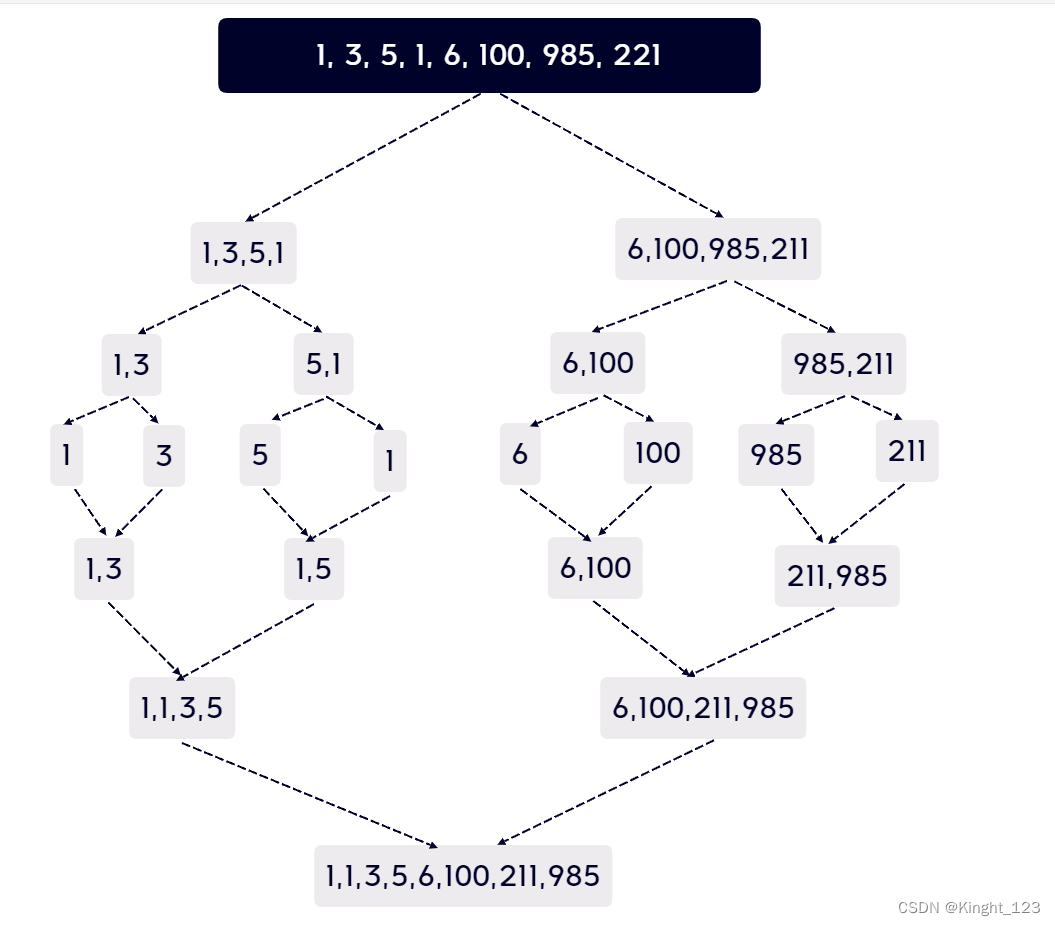
核心思想：

• 利用递归来进行归并排序，我们假设先把中间的数字提取出来，然后把左部分排好序，并且右部分也排好序，然后左部分和右部分重复之前的操作。
• 具体的排好序的过程。（merge函数）。注意：分成左部分和右部分这步操作非常的重要。
• 首先新建一个空的数组help，然后通过两个指针，第一个指针指向左部分的首位置，第二个指针指向最右部分的首位置。
• 然后开始排序，条件是：左指针小于中间的位置并且右指针小于右部分最右侧的位置；如果左部分的指针对应的数字小于右部分的指针对应的数字，那么数组help添加左部分对应的数字，左指针右移；否则，数组help添加右部分对应的数字，右指针右移。
• 然后结束之后，左指针或者右指针一点有一个指针没有到达最末尾的位置。所以需要把剩下的没有指到的部分数字依次添加到数组中。
• 最后把数组help拷贝到原来的数组中，至此代码结束。

二、C++代码

#include <iostream>
#include<vector>

using namespace std;


void merge(int* arr, int left, int mid, int right) {
	vector<int> help;
	int p1 = left;
	int p2 = mid + 1;
	int k = 0;
	while (p1 <= mid && p2 <= right) {
		if (arr[p1] <= arr[p2]) {
			help.push_back(arr[p1]);
			p1++;
		}
		else {
			help.push_back(arr[p2]);
			p2++;
		}
	}
	while (p1 <= mid) {
		help.push_back(arr[p1]);
		p1++;
	}
	while (p2 <= right) {
		help.push_back(arr[p2]);
		p2++;
	}
	for (int i = left; i <= right; i++) {
		arr[i] = help[k++];
	}
}

void merge_sort(int* arr, int left, int right) {
	if (left == right) return;
	int mid = left + ((right - left) >> 1);
	merge_sort(arr, left, mid);
	merge_sort(arr, mid + 1, right);
	merge(arr, left, mid, right);
}

int main() {
	int n, nums[INT16_MAX];
	cout << "请输入数列中的元素的个数n为：\n";
	cin >> n;
	cout << "请依次输入数列中的元素为：\n";
	for (int i = 0; i < n; i++) {
		cin >> nums[i];
	}
	merge_sort(nums, 0, n-1);
	cout << "归并排序的结果为：\n";
	for (int i = 0; i < 7; i++) {
		cout << nums[i] << " ";
	}
	return 0;
}

运行结果：

三、Python代码

# -*- coding: utf-8 -*-
# @Time        : 2024/1/17 14:34
# @File        : 归并排序.py
# @Description : None
# ----------------------------------------------
# ☆ ☆ ☆ ☆ ☆ ☆ ☆ 
# >>> Author    : Kinght_123
# >>> Mail      : 1304662247@qq.com
# >>> Blog      : tim1304662247.blog.csdn.net
# ☆ ☆ ☆ ☆ ☆ ☆ ☆
'''归并排序'''


def merge_sort(arr, left, right):
    if left == right:
        return
    mid = left + ((right - left) >> 1)
    merge_sort(arr, left, mid)
    merge_sort(arr, mid + 1, right)
    merge(arr, left, mid, right)


def merge(arr, left, mid, right):
    help = []
    p1 = left
    p2 = mid + 1
    while p1 <= mid and p2 <= right:
        if arr[p1] <= arr[p2]:
            help.append(arr[p1])
            p1 += 1
        else:
            help.append(arr[p2])
            p2 += 1
    while p1 <= mid:
        help.append(arr[p1])
        p1 += 1
    while p2 <= right:
        help.append(arr[p2])
        p2 += 1
    arr[left:right + 1] = help


if __name__ == '__main__':
    ls = [1, 3, 5, 1, 6, 100, 985, 221]
    merge_sort(ls, 0, len(ls) - 1)
    print(ls)

运行结果：