Python - 深夜数据结构与算法之 DP 串讲

news2024/11/15 11:16:58

一.引言

二.DP 知识点回顾

1.递归

2.分治

3.动态规划

三.DP 经典题目回顾

1.Climb-Stairs [70]

2.Unique-Paths [62]

3.House-Robber [198]

4.Min-Path-Sum [64]

5.Best-Time-Sell-Stock [121]

6.Min-Cost-Climb [746]

7.Edit-Distance [72]

8.Longest-Sub-Seq [300]

四.总结

一.引言

动态规划 DP 作为算法里比较晦涩难懂的一部分，我们这里多多复习几遍也不为过。本文主要重温递归、分治、回溯以及状态转移方程的概念，同时复习一下之前做过的题目。

二.DP 知识点回顾

1.递归

2.分治

3.动态规划

复杂的问题转换为子问题 - 分治 & 最优子结构 - 递推到 n :

三.DP 经典题目回顾

1.Climb-Stairs [70]

爬楼梯: https://leetcode-cn.com/problems/climbing-stairs/

◆ 题目分析

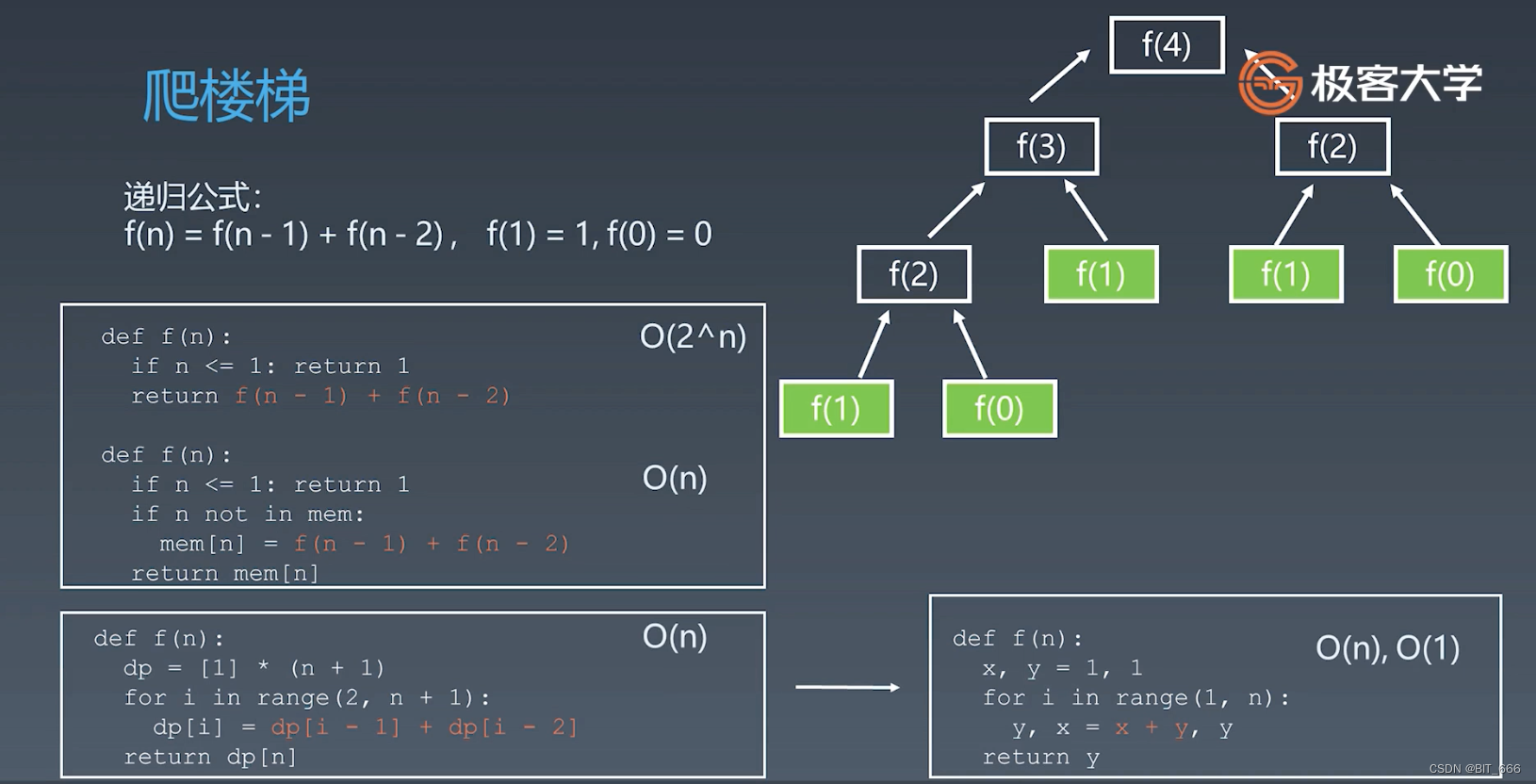
爬楼梯一次可以走1步或者2步，因此推导出 f(n) = f(n-1) + f(n-2)，与 Fib 异曲同工。

◆ 傻递归

class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n <= 2:
            return n
        
        return self.climbStairs(n-1) + self.climbStairs(n-2)

傻递归存在大量的重复计算，基本都会超时。

◆ 递归 + Cache

class Solution(object):

    def __init__(self):
        self.mem = {0:0, 1:1, 2:2}

    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n in self.mem:
            return self.mem[n]

        steps = self.climbStairs(n-1) + self.climbStairs(n-2)
        self.mem[n] = steps
        return self.mem[n]

加 Cache 的通法，在 init 初始化 cache，在傻递归返回的时候存入 cache 避免重复计算。

◆ DP Table

class Solution(object):

    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """

        if n <= 2:
            return n

        a, b = 1, 2
        for i in range(1, n):
            a, b = b, a+b
        
        return a

使用 DP Table 时如果只使用有限个状态，一般都可以使用几个变量完成 dp 推进。

2.Unique-Paths [62]

不同路径: https://leetcode.cn/problems/unique-paths/

◆ 题目思路

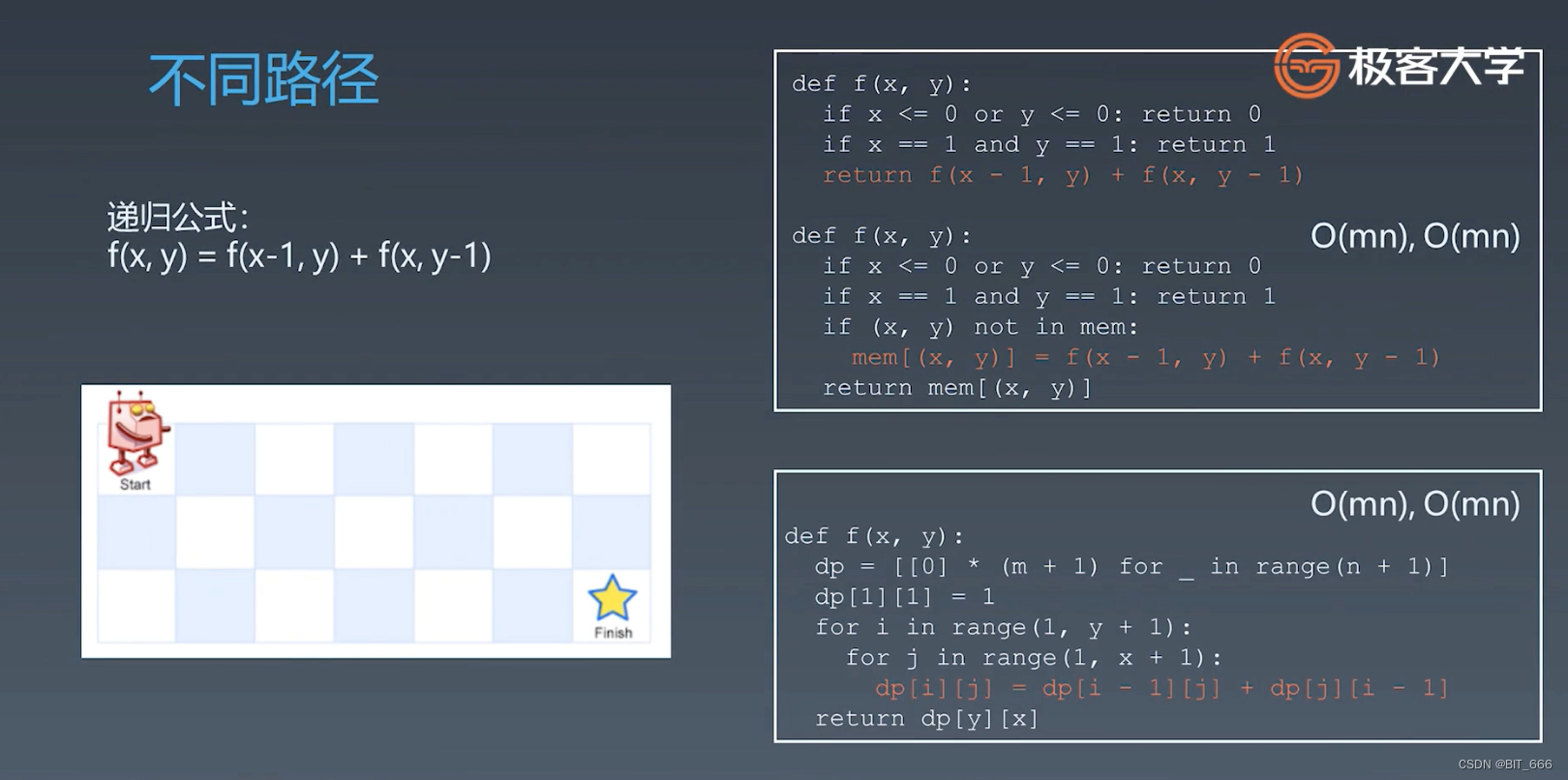
◆ DP Table

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """

        dp = [[0] * n for _ in range(m)]
        for i in range(n):
            dp[0][i] = 1

        for j in range(m):
            dp[j][0] = 1

        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]

        return dp[m-1][n-1]

dp[i][j] = dp[i-1][j] + dp[i][j-1] 即新位置等于左边和上面的位置之和。

◆ combination

class Solution(object):

    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """

        total = m + n - 2

        # 减少计算量
        if m > n:
            k = n - 1
        else:
            k = m - 1

        A = 1
        F = 1

        for i in range(k):
            A *= total
            total -= 1
            F *= k
            k -= 1

        return A // F

可以转化为排列组合问题，M+N-2 种走法，只要 M-1 向右，N-1 向下即可，直接套用 C(n,k)。

3.House-Robber [198]

打家劫舍: https://leetcode-cn.com/problems/house-robber/

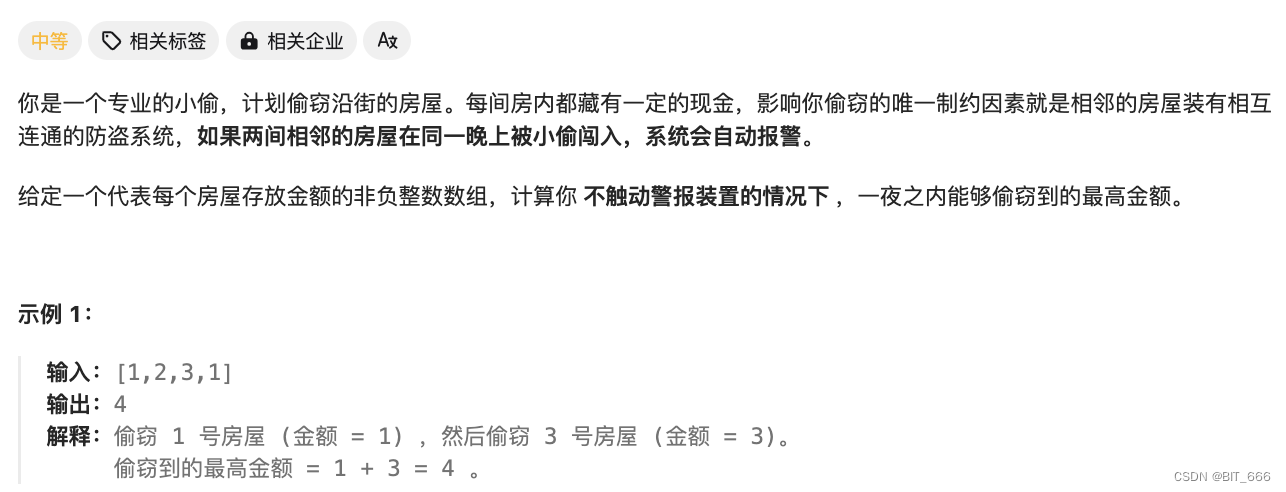
◆ 题目分析

◆ DP 转移

class Solution(object):
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """

        # 两个状态代表偷不偷
        dp = [[0, 0] for _ in range(len(nums))]
        dp[0][1] = nums[0]

        for i in range(1, len(nums)):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1])
            dp[i][1] = dp[i-1][0] + nums[i]
        
        return max(dp[-1][0], dp[-1][1])

[0]、[1] 两个状态代表偷或者不偷，遍历即可。

◆ 空间优化

class Solution(object):
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """

        pre, now = 0, 0

        for i in nums:
            pre, now = now, max(pre + i, now)

        return now

当前状态只与前两次状态有关，所以可以压缩 DP 状态空间。

4.Min-Path-Sum [64]

最小路径和: https://leetcode-cn.com/problems/minimum-path-sum/

◆ 题目分析

◆ DP 状态

class Solution(object):
    def minPathSum(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """

        M, N = len(grid), len(grid[0])

        # 遍历行
        for col in range(1, N):
            grid[0][col] += grid[0][col-1]

        # 遍历行
        for row in range(1, M):
            grid[row][0] += grid[row - 1][0]

        # 遍历内部元素
        for row in range(1, M):
            for col in range(1, N):
                grid[row][col] += min(grid[row - 1][col], grid[row][col - 1])
        
        return grid[M - 1][N - 1]

每一步的最小值等于当前位置加上左边或上面的最小值。

5.Best-Time-Sell-Stock [121]

股票买卖: https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/

◆ 题目分析

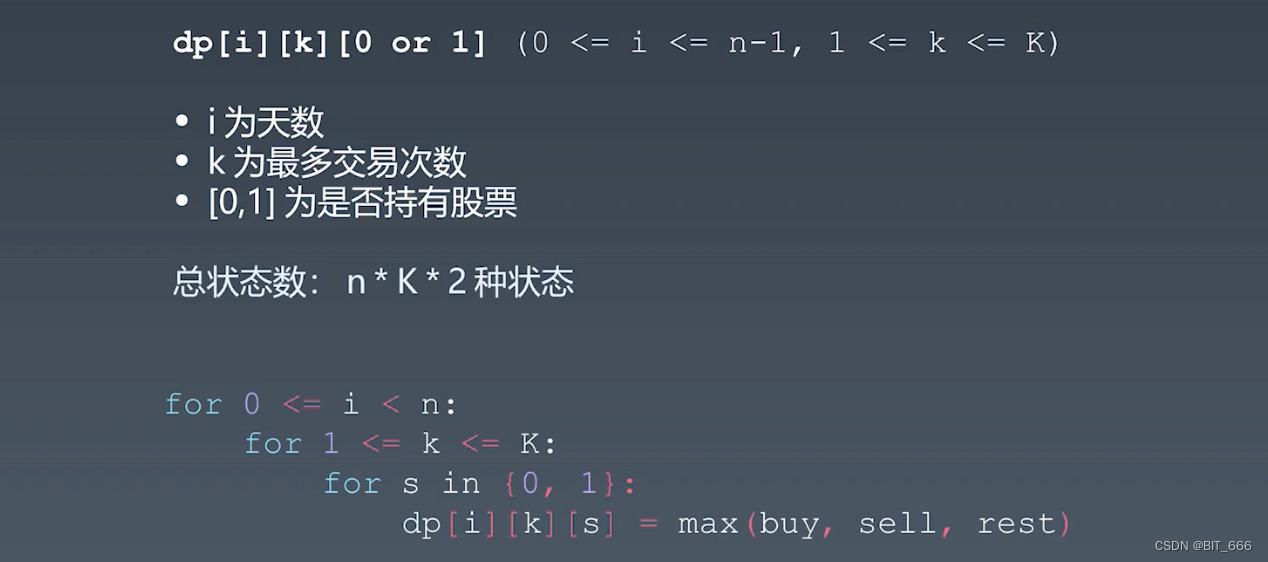
上面为股票问题的 dp 套路模版，其中 dp 空间 i 为天数，k 为交易次数，s 为是否持有股票。

要维持没有股票的状态，只能 rest 或者卖，要维持有股票的状态，只能 rest 或者买。

rest 代表保持状态，buy 时因为要从 Profit 中付出代价，所以要减去 prices[i]。

◆ DP 状态

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """

        # dp[i] = max(dp[i] - pre_min, dp[i-1])

        dp = [0] * len(prices)
        pre_min = prices[0]

        for i in range(1, len(prices)):
            dp[i] = max(prices[i] - pre_min, dp[i-1])
            if pre_min > prices[i]:
                pre_min = prices[i]

        return dp[-1]

dp[i] = max(dp[i] - pre_min, dp[i-1]) 当前位置等于卖了和上一次的最大值。

◆ DP + 双指针

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """

        # dp[i] = max(dp[i] - pre_min, 0)

        cur_min = prices[0]
        cur_max = 0

        for i in range(1, len(prices)):
            cur_max = max(cur_max, prices[i] - cur_min)
            cur_min = min(cur_min, prices[i])
        
        return cur_max

每次维护 max 和 min 即可。

6.Min-Cost-Climb [746]

最小花费爬楼梯: https://leetcode.cn/problems/min-cost-climbing-stairs/description/

◆ 题目分析

到达第 i 个楼梯，起点是 0 级或 1 级台阶。我们到达 i 级台阶的费用:

dp[i] = min(dp[i-1] + cost[i-1], dp[i-1] + cost[i-2])

由于起始点 0,1 都可以自由选择，所以其初始化为 0 。

◆ DP 实现

class Solution(object):
    def minCostClimbingStairs(self, cost):
        """
        :type cost: List[int]
        :rtype: int
        """

        # dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-1])

        dp = [0] * (len(cost) + 1)

        for i in range(2, len(cost) + 1):
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])

        return dp[-1]

这个题比较坑的点是楼顶对应索引 n，而索引从 0 开始，所以需要遍历 range(0, n+1)。不过题目的状态转移方程还是很漂亮，借鉴了前面爬楼梯的题目。

7.Edit-Distance [72]

编辑距离: https://leetcode-cn.com/problems/edit-distance/

◆ 题目分析

这个题和之前的单词接龙比较像，但是一拿到又无从下手，这里直接给出 DP 的思路，构建二维 DP 状态矩阵，大小为 [M+1, N+1]，如果 w1[i] == w2[j] 字符相同，那么此处无需操作；否则我们需要借助插入、删除、替换的操作，这里插入和删除其实是相对的，无需严格的区分:

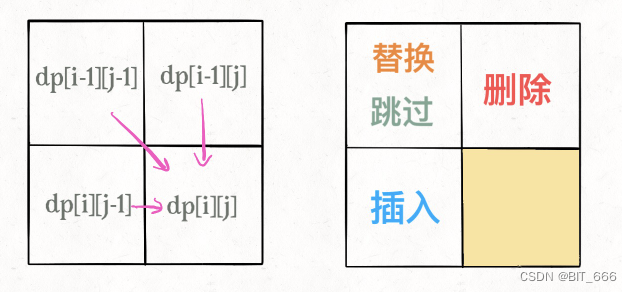
所以 dp[i][j] 的最小编辑距离就可以从 min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) 里找最小再 + 1。这个题好写但是难想，把上面的 dp table 写出来更方便理解，这里理解不好就记忆好了，也不错。

◆ DP 实现

class Solution(object):
    def minDistance(self, word1, word2):
        """
        :type word1: str
        :type word2: str
        :rtype: int
        """
        # w[i] = w[j] -> w[i][j] = w[i-1]w[j-1]
        # w[i] != w[j] -> w[i][j] = min(w[i-1][j-1] + 1, w[i-1][j] + 1, w[i][j-1] +1)

        M, N = len(word1), len(word2)

        # 状态空间
        dp = [[0] * (N + 1) for _ in range(M + 1)]

        #
        for i in range(M + 1):
            dp[i][0] = i
        for j in range(N + 1):
            dp[0][j] = j

        for i in range(1, M + 1):
            for j in range(1, N + 1):
                if word1[i - 1] == word2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1

        return dp[-1][-1]

8.Longest-Sub-Seq [300]

最长递增子序列: https://leetcode.cn/problems/longest-increasing-subsequence

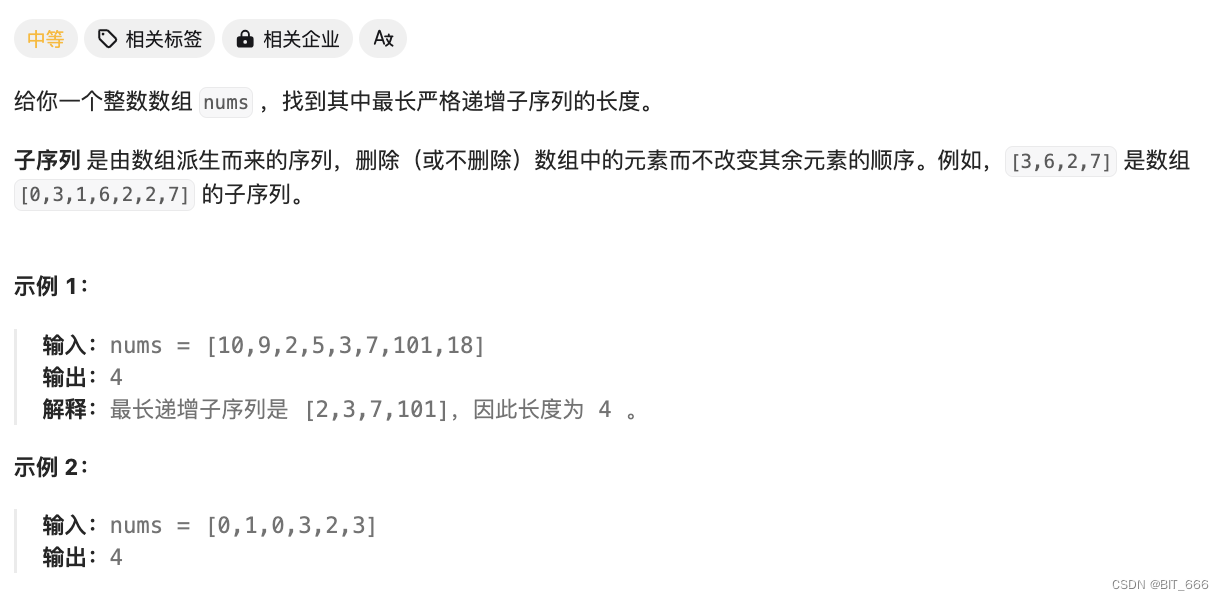
◆ 题目分析

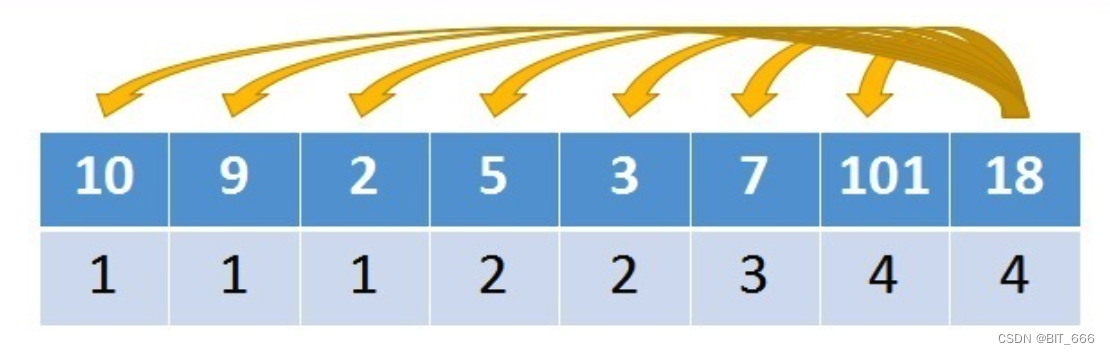
对于 i 位置，其等于 range(0, i) 之间的元素，如果 nums[i] > nums[j] 则 dp[i] = max_sub + 1。

◆ DP 实现

class Solution(object):
    def lengthOfLIS(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        dp = [1] * len(nums)

        for i in range(1, len(nums)):
            for j in range(0, i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)

        return max(dp)