目录
- 理论解读
- 状态机定义
- 状态转移图
- Mealy和Moore型状态机
- 推荐写“新两段式状态机”
- 设计实战
- 可乐机
- 两种state的FSM(异步复位)
- 4种状态的one-hot状态机
- 4种状态的同步复位状态机
- 蓄水池问题
- 参考链接
理论解读
状态机定义
- 状态机简写为 FSM(Finite State Machine),也称为同步有限状态机,简称为状态机,“同步”是指状态机中所有的状态跳转都是在时钟的作用下进行,而“有限”是指状态的个数是有限的。
- 状态机是时序逻辑电路中非常重要的一个应用,常在大型复杂的系统中使用较多。
- 为清晰表达出状态和状态跳转的条件,有必要绘制状态转移图!
- 写好状态机的三个关键步骤:
1、从实际问题中抽象出状态转移图
2、绘制状态转移图
3、根据状态转移图来设计代码
状态转移图
- 状态转移图需要表达的信息:各状态之间的功能、跳转的条件、输入输出
1、每个椭圆的框表示一个状态
2、每个状态之间都有一个指向的箭头,表示的是状态跳转的过程
3、箭头上有标注的一组数字,“/”左边表达的是状态的输入,“/”右边表达的是状态的输出
1、输入:根据输入可以确定是否需要进行状态跳转以及输出,是影响状态机系统执行过程
的重要驱动力;
2、输出:根据当前时刻的状态以及输入,是状态机系统最终要执行的动作;
3、状态:根据输入和上一状态决定当前时刻所处的状态,是状态机系统执行的一个稳定的
过程。
- 示例:可乐机
1、输入:投入 1 元硬币;
2、输出:出可乐、不出可乐;
3、状态:可乐机中有 0 元、可乐机中有 1 元、可乐机中有 2 元、可乐机中有 3 元。
Mealy和Moore型状态机
- 共同点:状态的跳转都只和输入有关
- 最后的输出和当前状态、输入有关,称为 Mealy 状态机(状态数最少),推荐

- 最后的输出和当前状态有关、与输入无关,则称为 Moore 型状态机

推荐写“新两段式状态机”
- 状态机按写法可分为:一段式、二段式、三段式
一段式指的是在一段状态机中使用时序逻辑既描述状态的转移,也描述数据的输出
二段式指在第一段状态机中使用时序逻辑描述状态转移,在第二段状态机中使用组合逻辑描述数据的输出
三段式指在第一段状态机中采用时序逻辑描述状态转移,在第二段在状态机中采用组合逻辑判断状态转移条件描述状态转移规律,在第三段状态机中描述状态输出,可以用组合电路输出,也可以时序电路输出
一段式在描述大型状态机时比较困难,不够清晰;
二段式状态机其结构与理想理论模型吻合,不会有附加的结构存在。 但是由于二段状态机的第二段是组
合逻辑描述数据的输出,所以有一些情况是无法描述的,比如输出时需要类似计数的累加情况,这种情况在组合逻辑中会产生自迭代,自迭代在组合逻辑电路中是严格禁止的,而且第二段状态机主要是描述数据的输出,输出时使用组合逻辑往往会产生更多的毛刺,所以并不推荐
三段式状态机的第一段状态机是用时序逻辑描述当前状态,第二段状态机是用组合逻辑描述下一状态,
- 新两段式状态机(本质是合并三段式的第一、二段,第三段不变):
在第一段状态机中:采用时序逻辑描述状态转移+在状态机中采用组合逻辑判断状态转移条件,描述状态转移规律
在第二段状态机中:描述状态输出,可以用组合电路输出,也可以时序电路输出
- 使用两个均采用时序逻辑的 always 块:
1、第一个 always 块描述状态的转移为第一段状态机,第二个 always 块描述数据的输出为第二段状态机
2、如果我们遵循一个 always 块只描述一个变量的原则,如果有多个输出时第二段状态机就可以分为多个
always 块来表达,但理论上仍属于新二段状态机,所以几段式状态机并不是由 always 块的数量简单决定的
设计实战
可乐机
- 状态转移图

- 代码设计
module simple_fsm (
input wire sys_clk , //系统时钟 50MHz
input wire sys_rst_n , //全局复位
input wire pi_money , //投币方式可以为:不投币(0)、投 1 元(1)
output reg po_cola //po_cola 为 1 时出可乐,po_cola 为 0 时不出可乐
);
//********************************************************************//
//****************** Parameter and Internal Signal *******************//
//********************************************************************//
//parameter define
//只有三种状态,使用独热码
parameter IDLE = 3'b001;
parameter ONE = 3'b010;
parameter TWO = 3'b100;
//reg define
reg [2:0] state ;
//********************************************************************//
//***************************** Main Code ****************************//
//********************************************************************//
//第一段状态机,描述当前状态 state 如何根据输入跳转到下一状态
always@(posedge sys_clk or negedge sys_rst_n)
if(sys_rst_n == 1'b0)
state <= IDLE; //任何情况下只要按复位就回到初始状态
else case(state)
IDLE : if(pi_money == 1'b1) //判断输入情况
state <= ONE;
else
state <= IDLE;
ONE : if(pi_money == 1'b1)
state <= TWO;
else
state <= ONE;
TWO : if(pi_money == 1'b1)
state <= IDLE;
else
state <= TWO;
//如果状态机跳转到编码的状态之外也回到初始状态
default: state <= IDLE;
endcase
//第二段状态机,描述当前状态 state 和输入 pi_money 如何影响 po_cola 输出
always@(posedge sys_clk or negedge sys_rst_n)
if(sys_rst_n == 1'b0)
po_cola <= 1'b0;
else if((state == TWO) && (pi_money == 1'b1))
po_cola <= 1'b1;
else
po_cola <= 1'b0;
endmodule
两种state的FSM(异步复位)
实现下图所示的摩尔状态机,复位为异步复位。

代码实现:
module top_module(
input clk,
input areset, // Asynchronous reset to state B
input in,
output out);//
parameter A=0, B=1;
reg state, next;
// State transition logic
always@(*)begin // This is a combinational always block
case(state)
A: next = in ? A : B;
B: next = in ? B : A;
endcase
end
// State flip-flops with asynchronous reset
always @(posedge clk or posedge areset) begin // This is a sequential always block
if(areset == 1'b1)begin
state <= B;
end else begin
state <= next;
end
end
// Output logic
assign out = (state == B);
endmodule
//写法2
module top_module(clk, reset, in, out);
input clk;
input reset; // Synchronous reset to state B
input in;
output out;//
reg out;
// Fill in state name declarations
parameter A=0, B=1;
reg state, next_state;
always @(*) begin // This is a combinational always block
case(state) // State transition logic
A:begin
if( in == 1'b1 )
next_state <= A;
else
next_state <= B;
end
B:begin
if( in == 1'b1 )
next_state <= B;
else
next_state <= A;
end
endcase
end
always @(posedge clk) begin // This is a sequential always block
if(reset)
state <= B;
else
state <= next_state;// State flip-flops with asynchronous reset
end
// Output logic
assign out = (state == B);
endmodule
- 验证结果

4种状态的one-hot状态机
- 实现下面的摩尔状态机,下表是状态转移图,一输入一输出四状态。使用以下 one-hot 状态编码:A=4’b0001, B=4’b0010, C=4’b0100, D=4’b1000。

- 代码设计
module top_module(
input in,
input [3:0] state,
output [3:0] next_state,
output out); //
parameter A=0, B=1, C=2, D=3;
// State transition logic: Derive an equation for each state flip-flop.
assign next_state[A] = state[A]&(~in) | state[C]&(~in);
assign next_state[B] = state[A]&(in) | state[B]&(in) | state[D]&(in);
assign next_state[C] = state[B]&(~in) | state[D]&(~in);
assign next_state[D] = state[C]&(in) ;
// Output logic:
assign out = state[D];
endmodule
4种状态的同步复位状态机
实现下面的摩尔状态机,状态转移图同上,一输入一输出四状态。
- 代码设计
module top_module(
input clk,
input in,
input reset,
output out); //
reg [1:0] state, next_state;
parameter A=2'd0, B=2'd1, C=2'd2, D=2'd3;
// State transition logic
always@(*)begin
case(state)
A: next_state = in ? B : A;
B: next_state = in ? B : C;
C: next_state = in ? D : A;
D: next_state = in ? B : C;
endcase
end
// State flip-flops with synchronous reset
always@(posedge clk)begin
if(reset == 1'b1)begin
state <= A;
end else begin
state <= next_state;
end
end
// Output logic
assign out = (state==D);
endmodule
蓄水池问题
一个巨大的蓄水池供几个用户使用。为了保持足够高的水位,三个传感器以5英寸的间隔垂直放置。当水位高于最高传感器(S3)时,输入流量应为零。当液位低于最低传感器(S)时,流量应处于最大值(公称流量阀和辅助流量阀都打开)。当水位位于上下传感器之间时,流量由两个因素决定: 水位和上次传感器更每个水位都有一个与之相关的标称流量,如下表所示。
如果传感器换之前水位的变化表明: 前一个液位低于当前液位,则应采用标称流量。如果前一个液位高于当前液位,则应通过打开补充流量阀(由AFR控制)来增加流量。
绘制水库控制器的摩尔模型状态图。清楚地指示每个状态的所有状态转换和输出。FSM的输入是Sy、S2和S3;输出是FR1、FR2、FR3和AFR。

- 代码设计
module top_module (
input clk,
input reset,
input [3:1] s,
output fr3,
output fr2,
output fr1,
output dfr
);
reg [3:0] state, next_state;
parameter in0=4'b111_1, in1=4'b011_0, in1_1=4'b011_1, in2=4'b001_0, in2_1=4'b001_1, in3=4'b000_0;
always@(*)begin
case(state)
in0 : next_state = s[1] ? in1 : in0; //111_1
in1 : next_state = s[2] ? in2 : (s[1] ? in1 : in0);//011_0
in1_1: next_state = s[2] ? in2 : (s[1] ? in1_1: in0);//011_1
in2 : next_state = s[3] ? in3 : (s[2] ? in2 : in1_1);//001_0
in2_1: next_state = s[3] ? in3 : (s[2] ? in2_1: in1_1);//001_1
in3 : next_state = s[3] ? in3 : in2_1; //000_0
default: ;
endcase
end
always@(posedge clk)begin
if(reset == 1'b1)begin
state <= in0;
end else begin
state <= next_state;
end
end
assign {fr3,fr2,fr1,dfr} = state;
/* always @(*)begin
case(state)
in0 :{fr3,fr2,fr1,dfr} = 4'b111_1;
in1 :{fr3,fr2,fr1,dfr} = 4'b011_0;
in1_1:{fr3,fr2,fr1,dfr} = 4'b011_1;
in2 :{fr3,fr2,fr1,dfr} = 4'b001_0;
in2_1:{fr3,fr2,fr1,dfr} = 4'b001_1;
in3 :{fr3,fr2,fr1,dfr} = 4'b000_0;
default:{fr3,fr2,fr1,dfr} = 'x;
endcase
end*/
endmodule
-
RTL图

-
状态转移图
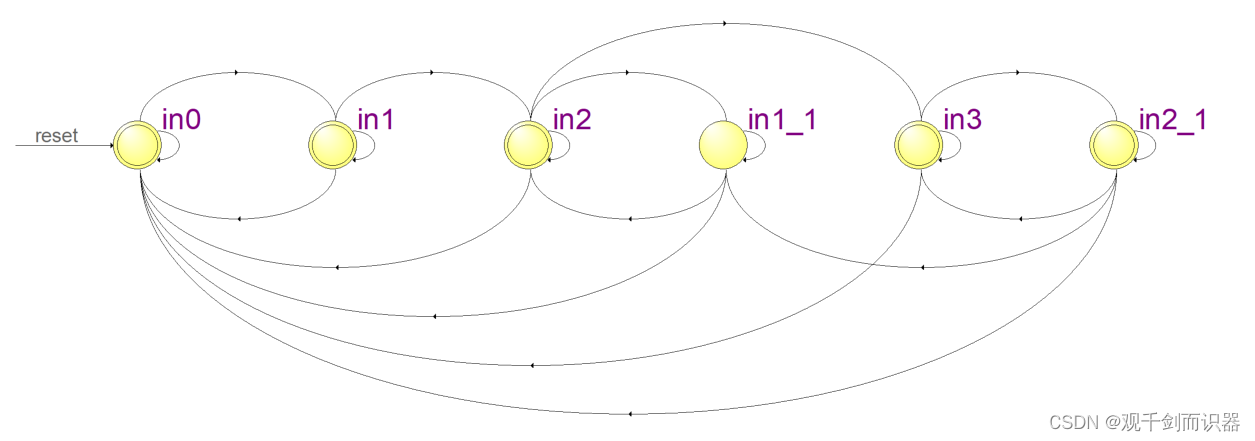
-
验证结果

参考链接
- 【野火】FPGA系列教学视频,真正的手把手教学,“波形图”教学法,现场画波形图写代码,硬件基于野火FPGA EP4CE10征途系列开发板,已完结
- Verilog零基础入门(边看边练)北京交通大学 李金城
- 《CMOS模拟集成电路全流程设计》 李金城 机械工业出版社