1.基本概念
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
2.具体操作
我们首先来看一段程序:
#include<iostream> using namespace std; int main(){ int n; cin>>n; for(int i=0;i<n;i++){ //~~~~~~~~~~ } return 0; }这段代码的时间复杂度是多少呢?上面也说了,就是他循环的次数。而程序中的for循环 的运行次数是n次。所以这段程序的时间复杂度为O(n)
#include<iostream> using namespace std; int main(){ int n; cin>>n; for(int i=3;i<n;i++){ //~~~~~~~~~~ } return 0; }那这段代码的时间复杂度是多少呢?难不成是O(n-3)?可能很多人都会有这样的疑问。其实在运算时间复杂度的过程中,会把程序里面的影响时间复杂度的数(不是变量!!!)全变成0。所以程序就变成了:
#include<iostream> using namespace std; int main(){ int n; cin>>n; for(int i=0;i<n;i++){//3变为0 //~~~~~~~~~~ } return 0; } 所以结果还是O(n)。
还有下面几段程序:
#include<iostream>
using namespace std;
int main(){
int a;
cin>>a;
cout<<a;
return 0;
}O(1) ,因为程序只运行了一遍
#include<iostream>
using namespace std;
int main() {
int n;
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
//~~~~~~~~~~~
}
}
return 0;
}O(n^2),因为程序执行了n的平方次。
其他的都一样,不过要注意的是,时间复杂度一般都只用字母来表示,如果你发现你的时间复杂度有数字(除平方外),比如什么O(3+n),O(n-4)什么的。肯定是你没有把数字去掉。
3.进阶方法
看完了基础的,我们来康康进阶的。
这个程序的时间复杂度是不是O(n^2+n)呢?其实不是。因为在计算时间复杂度的时候,我们往往只计算程序中最重要的部分。所以时间复杂度应为O(n^2)。#include<iostream> using namespace std; int main() { int n,a[100]; cin>>n; for(int i=0;i<n;i++){ cin>>a[i]; } for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ //~~~~~~~~ } } return 0; }
int binarySearch(int arr[], int left, int right, int target) { while (left <= right) { int mid = left + (right - left) / 2; if (arr[mid] == target) { return mid; } else if (arr[mid] < target) { left = mid + 1; } else { right = mid - 1; } } return -1; // 如果未找到目标值,则返回-1 }这段代码的时间复杂度是多少呢?熟悉二分算法的人都知道,二分算法最慢的要运行2分之一n次。但我们不知道它属于那种情况,怎么办呢?原来,在计算时间复杂度的时候,普遍使用最不理想的运算次数。所以时间复杂度就是O(logn)
log是什么?log可以理解成没法去掉数字得出的小于n的循环次数就用logn来表示。
下面再看最后一段代码:
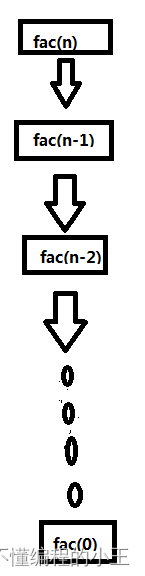
int factorial(int n) { if (n == 0) { return 1; } else { return n * factorial(n - 1); } }该来的总是来了,这个程序是递归,怎么算时间复杂度呢?其实很简单,只需要看这个函数被递归调用了几次就可以了。我们发现这个递归是这样的:
所以这个程序会运行n次,也就是O(n)了~~~