文章目录
- 一.设计模式
- 二.stack的模拟实现
- 三.queue的模拟实现
- 四.了解deque
- 五、题目练习
一.设计模式
设计模式有很多种,根据设计模式的参考书 Design Patterns - Elements of Reusable Object-Oriented Software(中文译名:设计模式 - 可复用的面向对象软件元素) 中所提到的,总共有 23 种设计模式。
设计模式是是前辈们对代码开发经验的总结,是解决特定问题的一系列套路,比如适配器模式,迭代器模式
迭代器模式:迭代器封装后提供统一的访问方式,不暴露底层的细节,迭代器实际上是一种设计模式。
适配器模式:适配器实际上是一种转换,通过已有的东西封装转换出你想要的东西
而栈与队列可以通过适配器模式进行实现。
数组可以通过vector和list进行转换
二.stack的模拟实现
stack.h
#pragma once
#include <vector>
#include <list>
namespace hwc
{
template<class T,class Container>
//template<class T,class Container=vector<T>>
class stack
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
const T& top()
{
return _con.back();
}
bool empty()
{
return _con.empty();
}
size_t size()
{
return _con.size();
}
private:
Container _con;
};
}
test.cpp
#include <iostream>
using namespace std;
#include "stack.h"
int main()
{
//hwc::stack<int, vector<int>> st;
hwc::stack<int,list<int>> st;
//hwc::stack<int> st
st.push(1);
st.push(2);
st.push(3);
st.push(4);
st.push(5);
while (!st.empty())
{
cout << st.top() << endl;
st.pop();
}
return 0;
}
三.queue的模拟实现
queue.h
#pragma once
#include <vector>
#include <list>
namespace hwc
{
template<class T,class Container=list<T>>
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
const T& front()
{
return _con.front();
}
const T& back()
{
return _con.back();
}
bool empty()
{
return _con.empty();
}
size_t size()
{
return _con.size();
}
private:
Container _con;
};
}
test.cpp
#include <iostream>
using namespace std;
#include "Queue.h"
int main()
{
hwc::queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
q.push(5);
while (!q.empty())
{
cout << q.front() << endl;
q.pop();
}
return 0;
}
四.了解deque
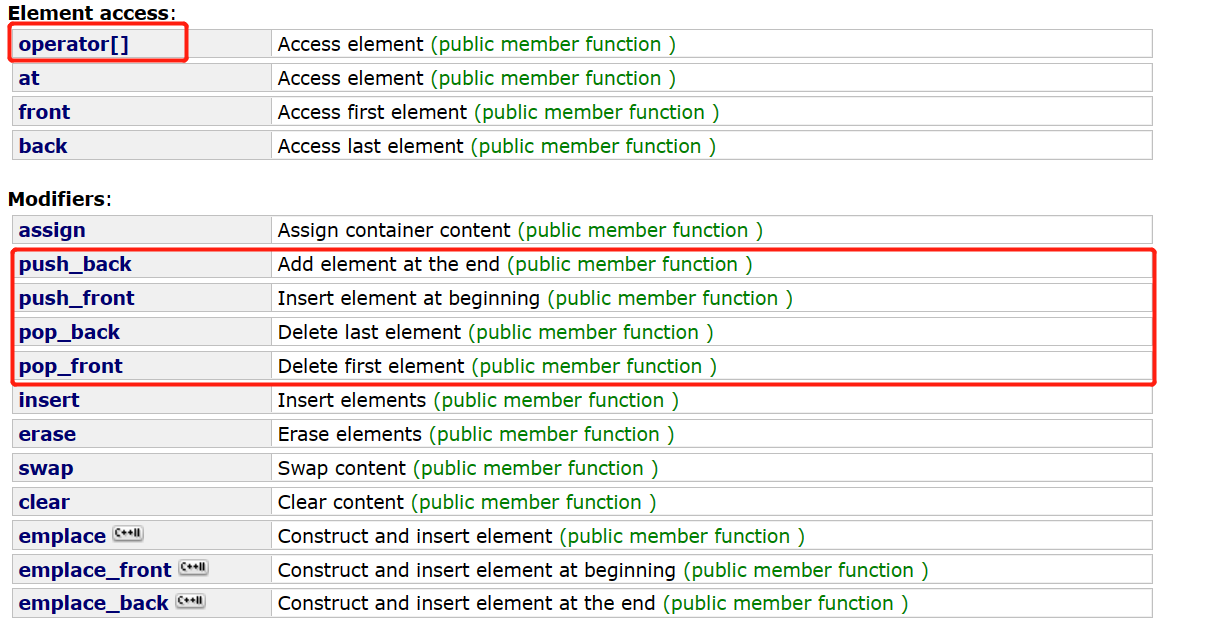
但是查看文档,Container发现用的并不是vector或是list,而是deque,申请空间做内存池


vector和list的结构都存在一些缺陷:vector真正的缺点在于扩容消耗,不支持头插头删,因为头部中部删除效率低。而list不支持随机访问,且CPU高速缓存命中率低,空间不连续。而deque兼具了vector和list的优点
int main()
{
deque<int> d;
d.push_back(1);
d.push_back(2);
d.push_back(3);
d.push_back(4);
d.push_front(10);
d.push_front(20);
for (size_t i = 0; i < d.size(); i++)
{
cout << d[i] << " ";
}
cout << endl;
return 0;
}

底层实现:deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的 ,为了避免扩容,由多个buffer数组构成,确定中控指针数组
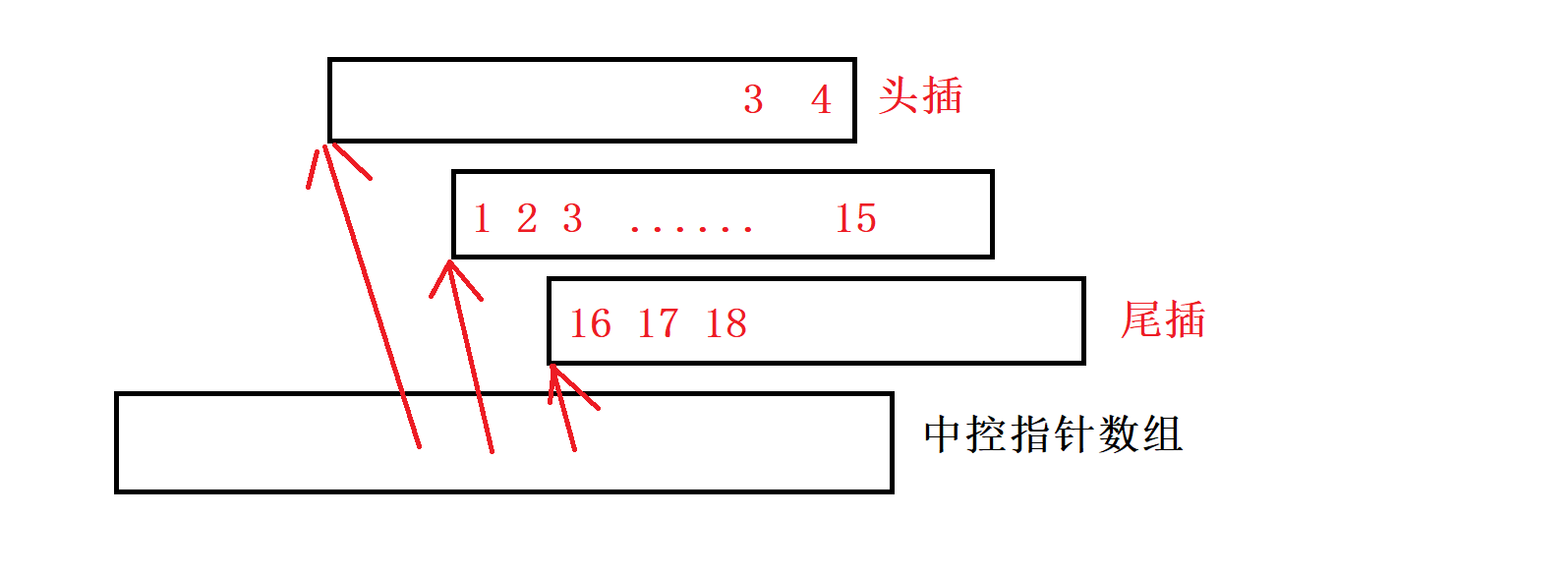
并不是说deque就是一定很完美,deque真正的问题在于随机访问的支持:算在第几个buffer在算在这个buffer的第几个。下标的随机访问有一定的消耗,没有vector的随机访问快。中间插入删除也有一定的消耗,相比list中间插入删除不够灵活,没有list快。
不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作为stack和queue**的底层数据结构
deque作为stack和queue的底层默认容器 :在stack中元素增长时,deque比vector的效率高(扩容时不需要搬移大量数据);queue中的元素增长时,deque不仅效率高,而且内存使用率高
五、题目练习
最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。示例 1:
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]输出:
[null,null,null,null,-3,null,0,-2]解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
class MinStack {
public:
MinStack() {
}
void push(int val) {
st.push(val);
if(minst.empty()|| val<=minst.top())
{
minst.push(val);
}
}
void pop() {
if(st.top() == minst.top())
{
minst.pop();
}
st.pop();
}
int top() {
return st.top();
}
int getMin() {
return minst.top();
}
stack<int> st;
stack<int> minst;
};
栈的压入、弹出序列
描述
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
0<=pushV.length == popV.length <=1000
-1000<=pushV[i]<=1000
pushV 的所有数字均不相同
示例1
输入:
[1,2,3,4,5],[4,5,3,2,1]返回值:
true说明:
可以通过push(1)=>push(2)=>push(3)=>push(4)=>pop()=>push(5)=>pop()=>pop()=>pop()=>pop() 这样的顺序得到[4,5,3,2,1]这个序列,返回true示例2
输入:
[1,2,3,4,5],[4,3,5,1,2]返回值:
false说明:
由于是[1,2,3,4,5]的压入顺序,[4,3,5,1,2]的弹出顺序,要求4,3,5必须在1,2前压入,且1,2不能弹出,但是这样压入的顺序,1又不能在2之前弹出,所以无法形成的,返回false
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
stack<int> ST;
for(int i = 0,j=0;i<pushV.size();i++)
{
ST.push(pushV[i]);
while(!ST.empty()&&ST.top()==popV[j])
{
ST.pop();
j++;
}
}
return ST.empty();
}
};
逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。示例 1:
输入:tokens = [“2”,“1”,“+”,“3”,“*”]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:输入:tokens = [“4”,“13”,“5”,“/”,“+”]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:输入:tokens = [“10”,“6”,“9”,“3”,“+”,“-11”,““,”/“,””,“17”,“+”,“5”,“+”]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(int i = 0;i<tokens.size();i++)
{
if(tokens[i]=="+"||tokens[i]=="-"||tokens[i]=="*"||tokens[i]=="/")
{
long long num1 = st.top();
st.pop();
long long num2 = st.top();
st.pop();
if(tokens[i]=="+") st.push(num2+num1);
if(tokens[i]=="-") st.push(num2-num1);
if(tokens[i]=="*") st.push(num2*num1);
if(tokens[i]=="/") st.push(num2/num1);
}
else
{
st.push(stoi(tokens[i]));
}
}
return st.top();
}
};