算法设计与分析
实验2
计科210X 甘晴void 202108010XXX

目录
文章目录
- 算法设计与分析<br>实验2
- 1 用动态规划法实现0-1背包
- 问题重述
- 想法
- 代码
- 验证
- 算法分析
- 2 用贪心算法求解背包问题
- 问题重述
- 想法
- 代码
- 验证
- 算法分析
- 3 半数集问题(实现题2-3)
- 问题重述
- 想法
- 代码
- 验证
- 算法分析
- 3.5 关于此题的进一步探索(半数单集问题,实现题2-4)
- 为什么会产生重复
- 如何消除重复
- 代码
- 验证
- 算法分析
- 4 集合划分问题(实现题2-7)
- 问题重述
- 验证方式
- ★基础知识补充
- 想法
- 算法1(贝尔数自身递推):
- 想法
- 代码
- 验证
- 算法分析
- 算法2(第二类斯特林数加和):
- 想法
- 代码
- 验证
- 算法分析
- 算法3(贝尔三角形):
- 想法
- 代码
- 验证
- 算法分析
- 继续深入
- 实验感悟
1 用动态规划法实现0-1背包
问题重述
一共有N件物品,第i(i从0开始)件物品的重量为weight[i],价值为value[i]。在总重量不超过背包承载上限maxw的情况下,求能够装入背包的最大价值是多少
想法
经典问题,假设我们现在手上有一个空的背包,然后从0个物品开始按照序号从小到大拿可供选择的物品,对于每个物品我们只有“选择”或者“不选择”两种策略。
状态dp[i][j]表示选择到第i个物品后,背包容量为j时所拿所有物品的最大价值。对于每一个物品而言,我们只有“拿”与“不拿”这两种处置方法。首先看看在当前状态下,如果腾空背包,能不能拿下它,如果即使背包空了都没法拿下它,那只能选择“不拿”,继承拿到前一个物品时这个大小的背包的状态;如果可能拿下它,那么我们可以选择“不拿”,跟前面一样处理,或者“拿”,这就要求腾出这个空间,但加上这个价格。
最优子结构易证:
假设(y1,y2,y3,……,yn)为所给01背包问题的一个最优解,则照理(y2,y3,……,yn)应该是其子问题的最优解。我们假设(y2,y3,……,yn)并不是其最优解,另存在(z2,z3,……,zn)为其子问题的最优解,那么一定有(y1,z2,z3,……,zn)为该问题的最优解,而非(y1,y2,y3,……,yn)是该问题的最优解,这与我们一开始的假设矛盾,故这是不成立的。所以该问题一定有最优子结构。
重叠子问题:
显然在计算i和j较大时的dp[i][j]必然会用到较小的dp[i][j]的值,故有重叠子问题。
这样,我们有状态转移方程如下:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
有了状态转移方程就可以写代码了。
代码
#include <stdio.h>
using namespace std;
int max(int a, int b)
{
return a > b ? a : b;
}
int solve(int n, int maxw, int weight[], int value[])
{
// weight[]重量
// value[]价值
int dp[n][maxw + 1];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < maxw + 1; j++)
{
dp[i][j] = 0;
}
}
for (int k = 0; k < maxw + 1; k++)
{
if (weight[0] <= k)
dp[0][k] = value[0];
}
for (int i = 1; i < n; i++)
{
for (int j = 0; j < maxw + 1; j++)
{
if (j - weight[i] < 0)
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
return dp[n - 1][maxw];
}
int main()
{
int n, maxw;
scanf("%d %d", &maxw, &n);
int w[n], v[n];
for (int i = 0; i < n; i++)
{
scanf("%d %d", &w[i], &v[i]);
}
printf("%d\n", solve(n, maxw, w, v));
}
验证
洛谷P1048 [NOIP2005 普及组] 采药(https://www.luogu.com.cn/problem/P1048)与这道题较为类似。
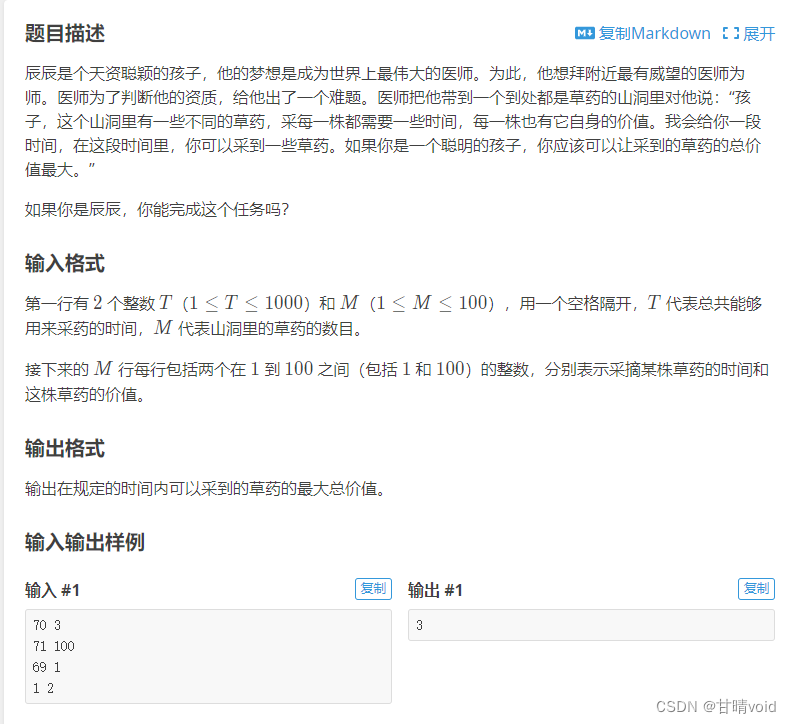
基本上是一模一样的,我们可以测试一下,结果如下:
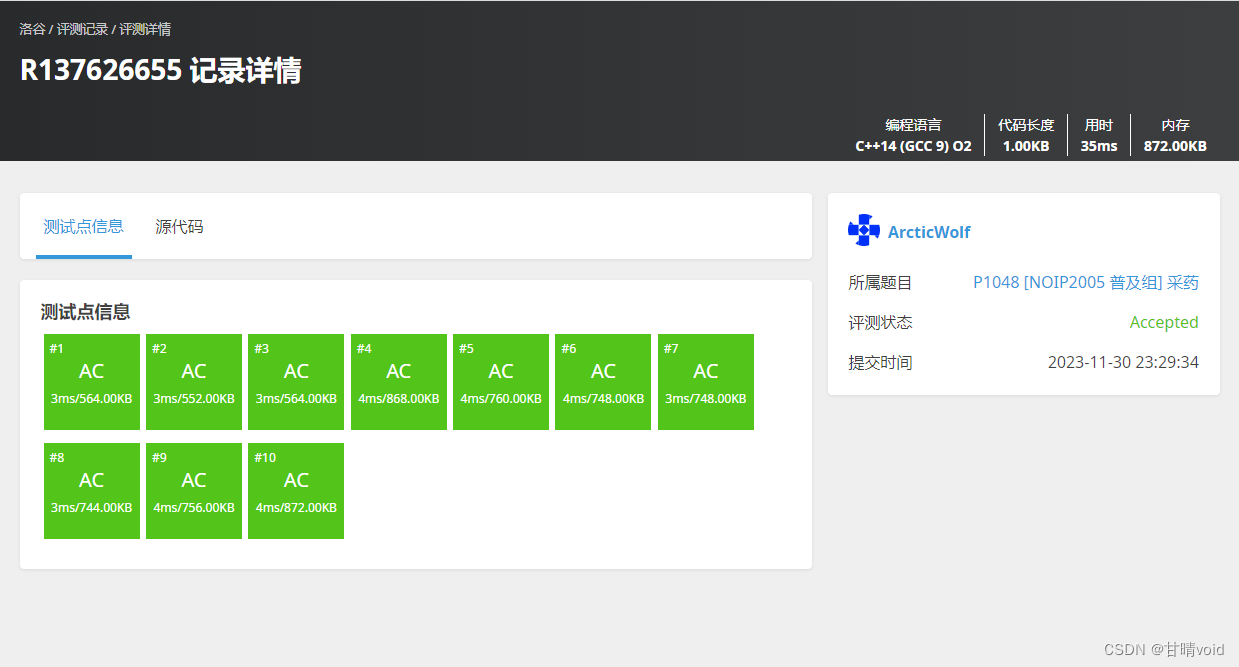
可见算法正确。
算法分析
时间复杂度O(nm),n为物品个数,m为最大背包容量。
空间复杂度O(nm),开了个这个数组。
2 用贪心算法求解背包问题
问题重述
有n个物品,每个物品的重量weight[i]和价格value[i],物品可以被分割,背包容量maxw,求最多拿走价值为多少。
想法
贪心背包和01背包,区别就在于“可以分割”,那么贪心策略就变为了优先取走“性价比”较高的物品,并按照这样的策略尽可能多的取走物品,如果能取走就尽可能取走,最后一个物品如果取不走,就分割取走可以取走的部分。
代码
#include <algorithm>
#include <stdio.h>
using namespace std;
struct object
{
int weight;
int value;
double vpw; // value per weight
};
bool cmp(struct object a, struct object b)
{
return a.vpw > b.vpw;
}
double solve_greedy(int n, int maxw, int weight[], int value[])
{
// weight[]重量
// value[]价值
struct object x[n];
for (int i = 0; i < n; i++)
{
x[i].weight = weight[i];
x[i].value = value[i];
x[i].vpw = (double)x[i].value / x[i].weight;
}
sort(x, x + n, cmp);
int total = 0; // 已放入背包的重量
double ans = 0; // 放入背包的价值
for (int i = 0; i < n; i++)
{
if (total + x[i].weight <= maxw)
{
ans += x[i].value;
total += x[i].weight;
}
else
{
ans += (((double)(maxw - total) / x[i].weight) * x[i].value);
break;
}
}
return ans;
}
int main()
{
int n, maxw;
scanf("%d %d", &n, &maxw);
int w[n], v[n];
for (int i = 0; i < n; i++)
{
scanf("%d %d", &w[i], &v[i]);
}
printf("%.2lf\n", solve_greedy(n, maxw, w, v));
}
验证
洛谷 P2240 【深基12.例1】部分背包问题(https://www.luogu.com.cn/problem/P2240)就是这个问题
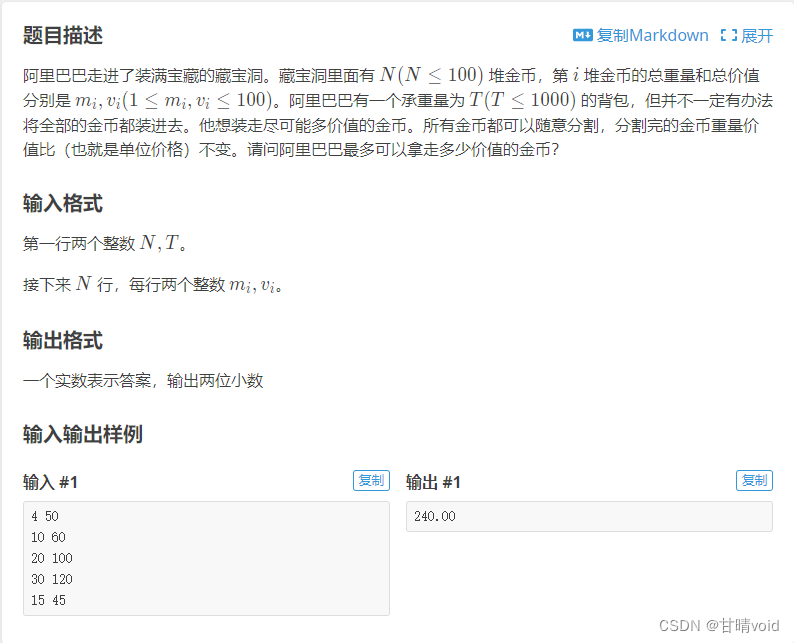
测试,结果如下。
通过了测试点。
算法分析
主要瓶颈在于排序,调用sort函数,按快速排序计,时间复杂度O(nlogn)。
空间复杂度考虑开了个数组,和结构体数组,是一维的,O(n)。
3 半数集问题(实现题2-3)
问题重述
给定一个自然数 n,由 n 开始可以依次产生半数集 set(n)中的数如下。
-
(1) n∈set(n);
-
(2) 在 n 的左边加上一个自然数,但该自然数不能超过最近添加的数的一半;
-
(3) 按此规则进行处理,直到不能再添加自然数为止。
例如,set(6)={6,16,26,126,36,136}。半数集 set(6)中有 6 个元素。
注意半数集是多重集。
编程任务:
- 对于给定的自然数 n,编程计算半数集 set(n)中的元素个数。
数据输入:
- 输入数据由文件名为 input.txt 的文本文件提供。
- 每个文件只有 1 行,给出整数 n。(0<n<1000)
结果输出:
- 程序运行结束时,将计算结果输出到文件 output.txt 中。输出文件只有 1 行,给出半数集 set(n)中的元素个数。
想法
问题有些复杂的时候可以先举例子。
例如.set(6) 6,16,26,126,36,136。半数集set(6)中有6个元素。
例如.set(10) 10,510,2510,12510,1510,410,2410,12410,1410,310,1310,210,1210,110,半数集set(10)中有14个元素。
设set(n)中的元素个数为f(n)。如:6的前面可以加上1、2、3,而2、3的前面又都可以加上1,也就是f(6)=1+f(3)+f(2)+f(1)。
则显然有递归表达式:f(n)=1+∑f(i),i=1,2……n/2。
可以先写一个递归函数如下
int f(int n)
{
int temp=1;
if(n>1)
for (int i=1;i < = n/2;i ++)
temp+=f(i);
return temp;
}
时间复杂度:n/2个相加,每一个需要计算1+…+i/2,因此时间复杂度为O(n^2)缺点:这样会有很多的重复子问题计算。
这个问题显然存在重叠子问题:例如,当n=4时,f(4)=1+f(1)+f(2),而f(2)=1+f(1),在计算f(2)的时候又要重复计算一次f(1)。如果这样的话时间复杂度会很大,我们要想办法简化重叠部分的计算。
可以采用“备忘录”的方法,来避免重叠部分的计算。
代码
#include <algorithm>
#include <stdio.h>
using namespace std;
int solve(int f[], int n)
{
if (n == 1)
return 1;
if (f[n] != 0)
return f[n];
int sum = 1;
for (int i = 1; i <= n / 2; i++)
sum += solve(f, i);
f[n] = sum;
return sum;
}
int main()
{
int n;
scanf("%d", &n);
int f[n + 1];
for (int i = 1; i <= n; i++)
f[i] = 0;
printf("%d\n", solve(f, n));
}
验证
P1028 [NOIP2001 普及组] 数的计算(https://www.luogu.com.cn/problem/P1028)
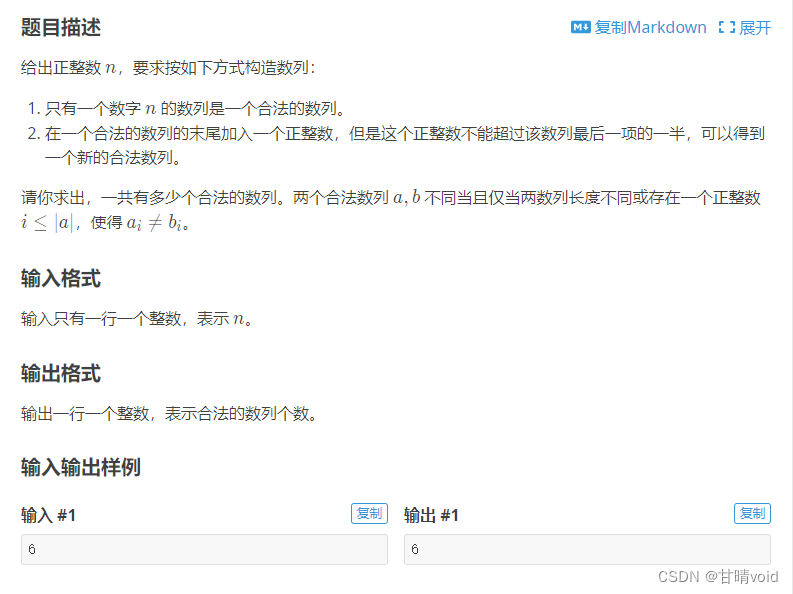
测试结果如下:
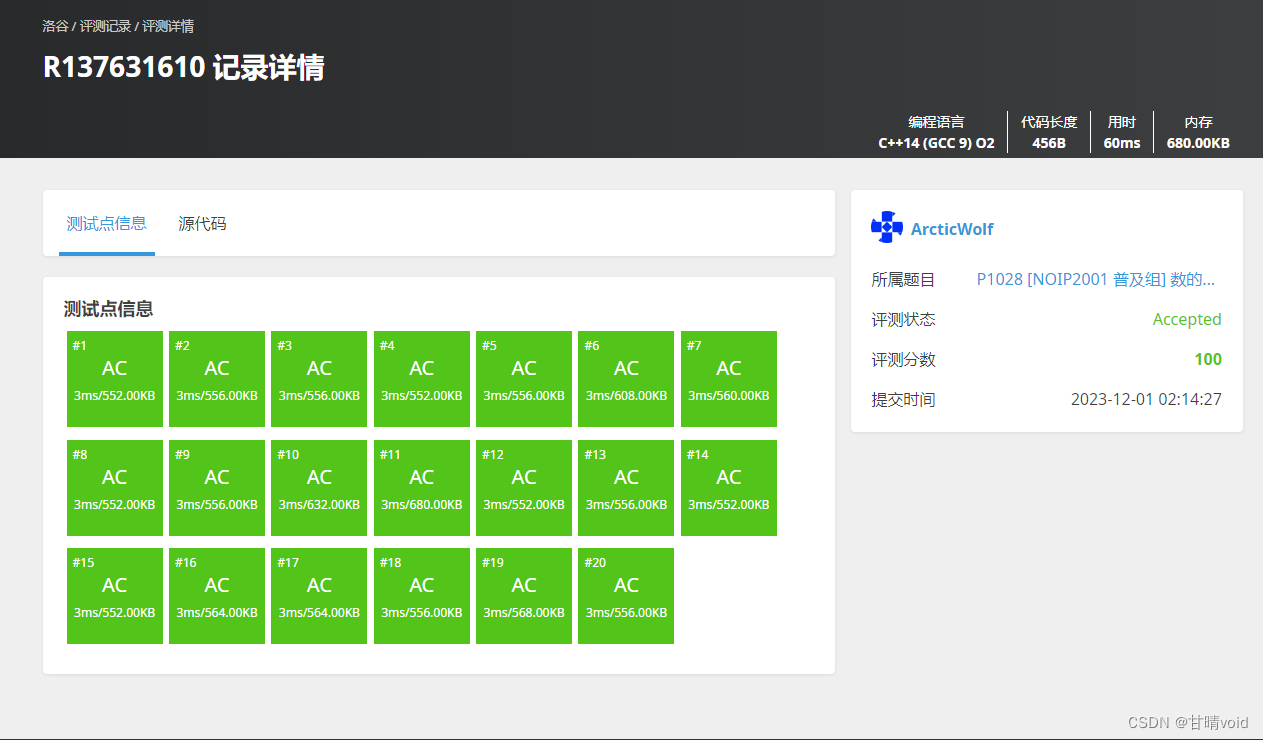
算法分析
使用到记忆化剪枝,本质上仍然是对每个f[i]都去遍历了f[0]到f[n/2],所以时间复杂度应该是O(n^2)。
由于开了备忘录数组,空间复杂度O(n)。
3.5 关于此题的进一步探索(半数单集问题,实现题2-4)
为什么会产生重复
2-3和2-4的唯一区别就在这个地方。2-4需要剔除重复的部分。
先来看看重复的部分是怎么产生的:
考虑n=26时的set(n)因为n/2=13,所以13 26∈set(n)但是我们想,1326真的只能这样产生嘛?
考虑26->3 26->1 3 26,也就是说26直接产生3再产生1,这是不是也可以。
这就造成了重复:[1][3][26] 和 [13][26] 都会产生 1326
现在我们要解决这个问题
如何消除重复
如果这道题仍然对n限定很高,那么是不好做的。
但是这里题目限定(0<n<201)这意味着0<n/2<=100,所以可能造成问题的必定是两位数。
我们再看刚刚的例子1326,如果是1226还会发生这样的事情嘛?如果是1126呢?
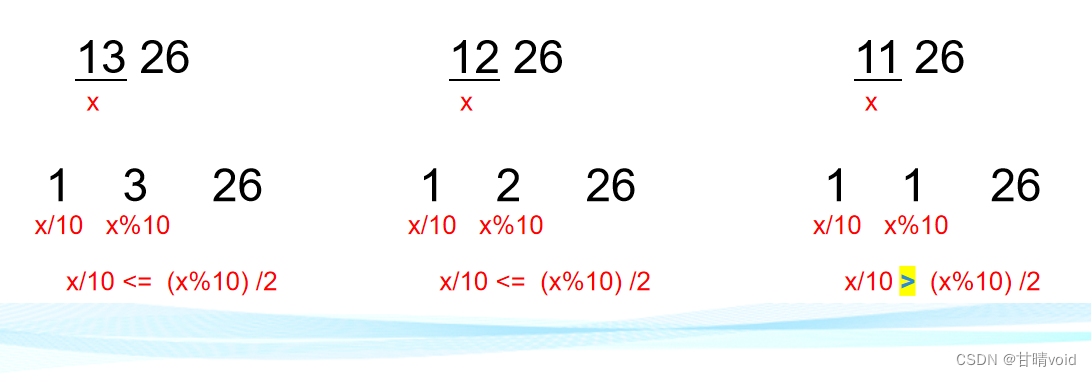
其实我们很好理解为什么【x/10 <= (x%10) /2】会出现重复的情况
因为这会导致(x%10)这一项仍然有能力分出它前面的那个
也就是1326的3,依旧具备产生1的能力,
而1126的右边的1,已经不具备再产生左边的1的能力了。
所以也就是说只有【x/10 <= (x%10) /2】这个情况会出现额外计数的分支,
那我们只需要再这个情况发生的时候,去剪掉由这个产生的分支就可以。
体现在算法上就是在算这一层的答案的时候减掉f[i/10]就好(当i/10*2<=i%10的时候)
代码
#include <algorithm>
#include <stdio.h>
using namespace std;
int solve(int f[], int n)
{
if (n == 1)
return 1;
if (f[n] != 0)
return f[n];
int sum = 1;
for (int i = 1; i <= n / 2; i++)
{
sum += solve(f, i);
if ((i > 10) && (2 * (i / 10) <= (i % 10)))
{
sum -= f[i / 10];
}
}
f[n] = sum;
return sum;
}
int main()
{
int n;
scanf("%d", &n);
int f[n + 1];
for (int i = 1; i <= n; i++)
f[i] = 0;
f[1] = 1;
printf("%d\n", solve(f, n));
}
验证
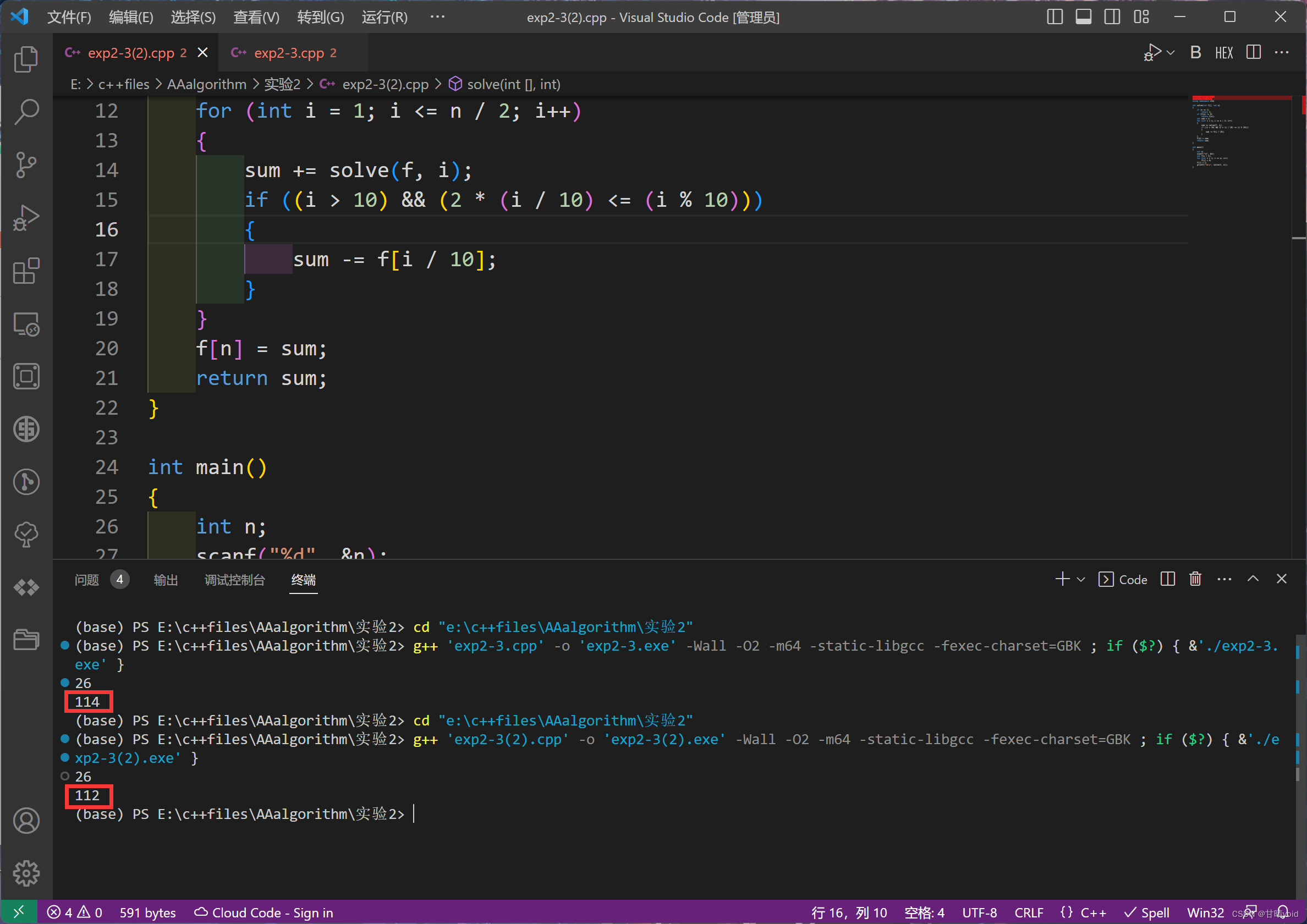
可以看到,对于我们刚刚给出的例子,[13][26]和[12][26]被删去了,效果实现了。
算法分析
由于本题只是进行了一句判断并剪枝,故与上一题一样
使用到记忆化剪枝,本质上仍然是对每个f[i]都去遍历了f[0]到f[n/2],所以时间复杂度应该是O(n^2)。
由于开了备忘录数组,空间复杂度O(n)。
4 集合划分问题(实现题2-7)
问题重述
n 个元素的集合{1,2,……, n }可以划分为若干个非空子集。例如,当 n=4 时,集合{1,2,3,4}可以划分为 15 个不同的非空子集如下:
{{1},{2},{3},{4}},
{{1,2},{3},{4}},
{{1,3},{2},{4}},
{{1,4},{2},{3}},
{{2,3},{1},{4}},
{{2,4},{1},{3}},
{{3,4},{1},{2}},
{{1,2},{3,4}},
{{1,3},{2,4}},
{{1,4},{2,3}},
{{1,2,3},{4}},
{{1,2,4},{3}},
{{1,3,4},{2}},
{{2,3,4},{1}},
{{1,2,3,4}}
编程任务:
给定正整数 n,计算出 n 个元素的集合{1,2,……, n }可以划分为多少个不同的非空子集。
数据输入:
由文件 input.txt 提供输入数据。文件的第 1 行是元素个数 n。
结果输出:
程序运行结束时,将计算出的不同的非空子集数输出到文件 output.txt 中。
验证方式
本题的验证由在线评测进行
洛谷P5748 集合划分计数(https://www.luogu.com.cn/problem/P5748)
注意与课本题面区别:
- 由于数据很大,题目要求取模
- 有多组数据
★基础知识补充
【贝尔数】
B[n]的含义是基数为 n的集合划分成非空集合的划分数。
贝尔数自身递推关系: B[n+1] = ∑ C(n,k) B[k] ,其中k从0到n。
其中定义B[0] = 1
【第二类斯特林数】
第二类斯特林数实际上是集合的一个拆分,表示将 n个不同的元素拆分成m个集合间有序(可以理解为集合上有编号且集合不能为空)的方案数,记为 S(n,m) (这里是大写的)或者 {n m} (n在上m在下) 。
和第一类斯特林数不同的是,这里的集合内部是不考虑次序的,而圆排列圆的内部是有序的。常常用于解决组合数学中的几类放球模型。描述为:将n个不同的球放入m个无差别的盒子中,要求盒子非空,有几种方案。
S(n,k)的值可以递归的表示为:S(n+1, k) = kS(n, k) + S(n, k-1)。
递推边界条件:
S(n,n) = 1, n>=0
S(n,0) = 0, n>=1
为什么会这样表示呢?当我们将第(n + 1)个元素添加到k个划分集合时,有两种可能性。
- 第n + 1个元素作为一个单独的集合参与到划分成k个集合,有S(n,k-1)个。
- 将第n + 1个元素添加到已经划分的k个集合中,一共有k*S(n,k)种。
【贝尔数与第二类斯特林数的关系】
B[n]=∑S(n,k) 其中k从0到n
参考资料:
【详细讲解第一二三类斯特林数】https://zhuanlan.zhihu.com/p/350774728
【详细讲解贝尔数和贝尔三角形】https://www.cnblogs.com/lfri/p/11549652.html
想法
这是一道数论模板题,相关的知识是【贝尔数】,本题只要根据给定的n求出贝尔数B[n]即可。
结合我们上面给出的基础知识,这里至少有以下几种求贝尔数的方法:
- 算法1:利用贝尔数自身递推关系,循环计算贝尔数
- 算法2:利用贝尔数与第二类斯特林数的关系,k从0到n计算S(n,k)并且累加求和。
- 算法3:使用贝尔三角形(后面讲)
下面逐个分析这些想法:
算法1(贝尔数自身递推):
想法
主要需要解决的是组合数的计算,数据量较小的时候可以用杨辉三角来计算组合数,数据量较大的时候可能会超时。
可以使用动态规划来计算组合数。
// 计算组合数的代码
#include <iostream>
#include<bits/stdc++.h>
#define ll long long
const int N = 55;
using namespace std;
ll ans[N][N];
void Combinations() //处理组合数
{
ans[0][0]=1;
for(int i=1;i<=40;i++)
{
ans[i][0]=1;
for(int j=1;j<=i;j++)
{
ans[i][j]=ans[i-1][j]+ans[i-1][j-1];
}
}
}
int main()
{
ll t;
cin>>t;
Combinations(); //记忆化搜索
ll a,b;
cin>>a>>b;
cout<<ans[a][b]<<endl;
return 0;
}
解决了组合数的计算之后,就可以再利用递推关系,把贝尔数求出来。用到如下关系:
-
贝尔数自身递推关系: B[n+1] = ∑ C(n,k) B[k] ,其中k从0到n。
-
其中定义B[0] = 1
代码
#include <bits/stdc++.h>
#define ll long long
const int N = 1000;
const int mod = 998244353;
using namespace std;
ll C[N][N];
ll B[N];
void Combinations() // 处理组合数
{
C[0][0] = 1;
for (int i = 1; i <= N - 1; i++)
{
C[i][0] = 1;
for (int j = 1; j <= i; j++)
{
C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
}
}
}
long long Bell(int n)
{
if (n == 0)
return 1;
ll ans = 0;
for (int k = 0; k <= n - 1; k++)
{
if (B[k] == 0)
B[k] = Bell(k);
ans += (C[n - 1][k] * B[k] % mod);
}
return ans % mod;
}
int main()
{
Combinations(); // 记忆化搜索求所有C(n,m)
for (int i = 0; i < N; i++)
B[i] = 0;
B[0] = 1;
int n, T;
scanf("%d", &T);
for (int i = 0; i < T; i++)
{
scanf("%d", &n);
printf("ans = %lld\n", Bell(n));
}
return 0;
}
验证
案例数据是可以过的。
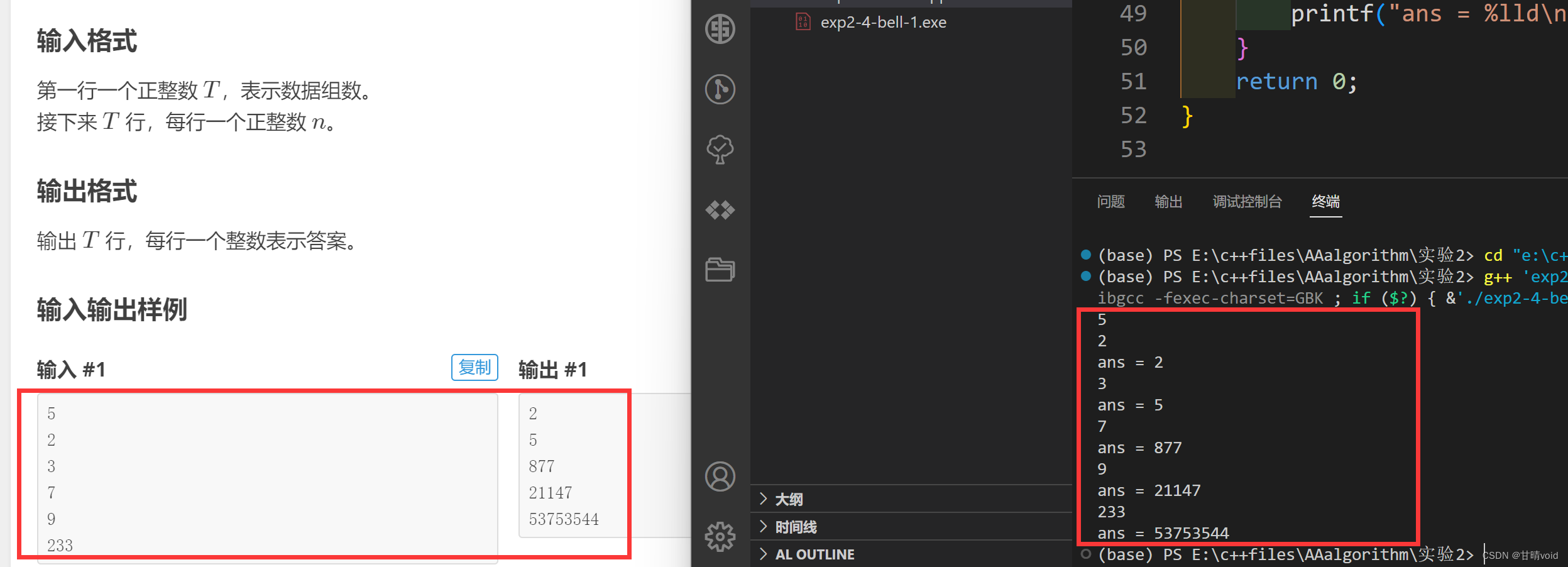
但是无法通过在线评测,这是因为我们要求的空间太大了。
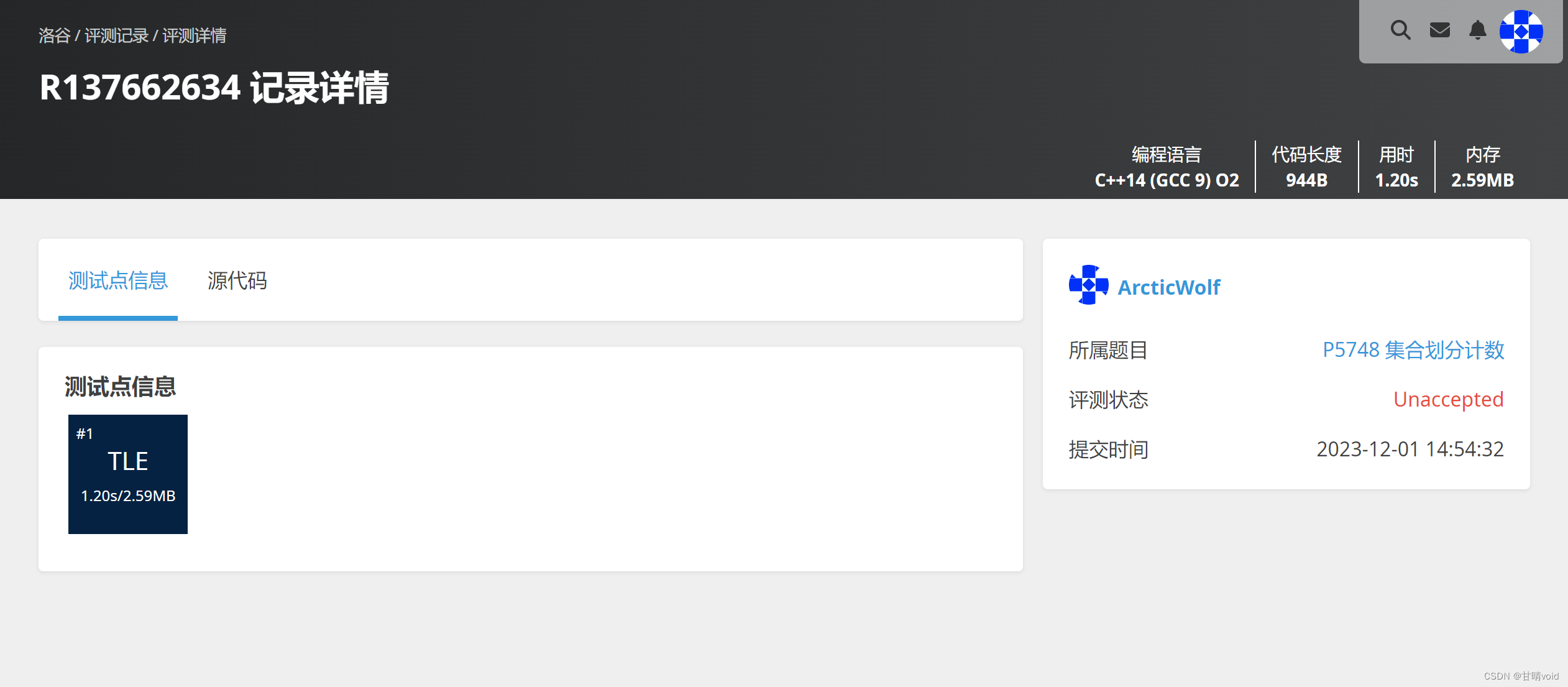
但是数据确实要求到了这么大,如果我们开小数据,会出现运行时错误(要求的位置越界了)
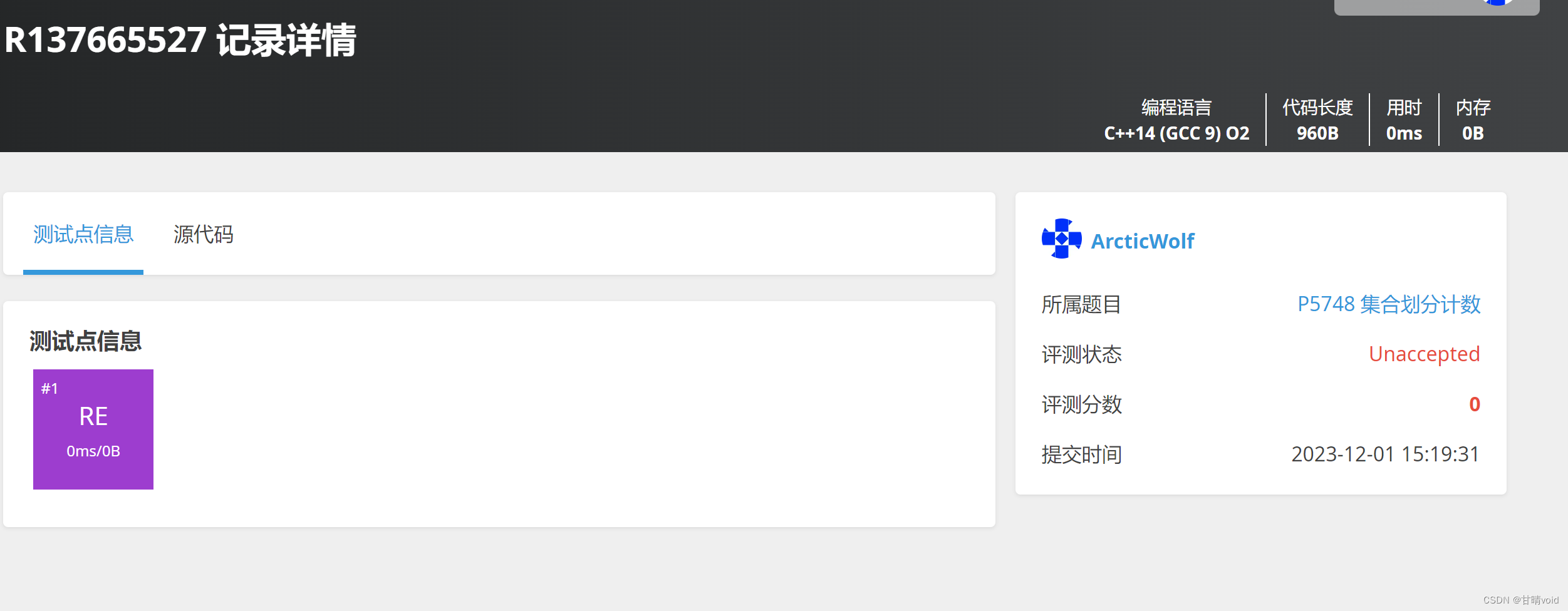
说明这种O(n^2)的方法无法通过。
算法分析
时间复杂度O(n^2)
空间复杂度O(n^2),但是递归消耗的栈空间实在太大了。
不可接受。
(时间足够多,空间足够大的时候可以考虑)
算法2(第二类斯特林数加和):
想法
主要的问题在于使用递推关系求出第二类斯特林数,再把第二类斯特林数加和得到贝尔数。
// 计算第二类斯特林数
typedef long long ll;
typedef int itn;
const int N = 5007, mod = 1e9 + 7;
int n, m, k;
int S[N][N];
int main()
{
scanf("%d%d", &n, &k);
S[0][0] = 1;
S[n][0] = 0;
for(int i = 1; i <= n; ++ i) {
for(int j = 1; j <= k; ++ j) {
S[i][j] = (S[i- 1][j - 1] + 1ll * j * S[i - 1][j]) % mod;//公式中的 k 是当前的 k
}
}
cout << S[n][k] << endl;
return 0;
}
计算出第二类斯特林数之后,通过这个关系:
- B[n]=∑S(n,k) 其中k从0到n
求解出B[n]
代码
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
typedef long long ll;
typedef int itn;
const int N = 5000;
const int mod = 998244353;
int n, m, k;
ll S[N][N];
ll B[N];
int solve_S(int n, int k)
{
S[0][0] = 1;
S[n][0] = 0;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= k; ++j)
{
S[i][j] = (S[i - 1][j - 1] + 1ll * j * S[i - 1][j]) % mod; // 公式中的 k 是当前的 k
}
}
return 0;
}
ll Bell(int n)
{
if (n == 0)
return 1;
ll ans = 0;
for (int k = 0; k <= n; k++)
{
if (!S[n][k])
solve_S(n, k);
ans += S[n][k];
ans = ans % mod;
}
return ans;
}
int main()
{
for (int i = 0; i < N; i++)
B[i] = 0;
B[0] = 1;
int n, T;
scanf("%d", &T);
for (int i = 0; i < T; i++)
{
scanf("%d", &n);
// printf("ans = %lld\n", Bell(n));
printf("%lld\n", Bell(n));
}
return 0;
}
验证
验证可得,案例同样可以过,空间不会超,但是还是TLE。
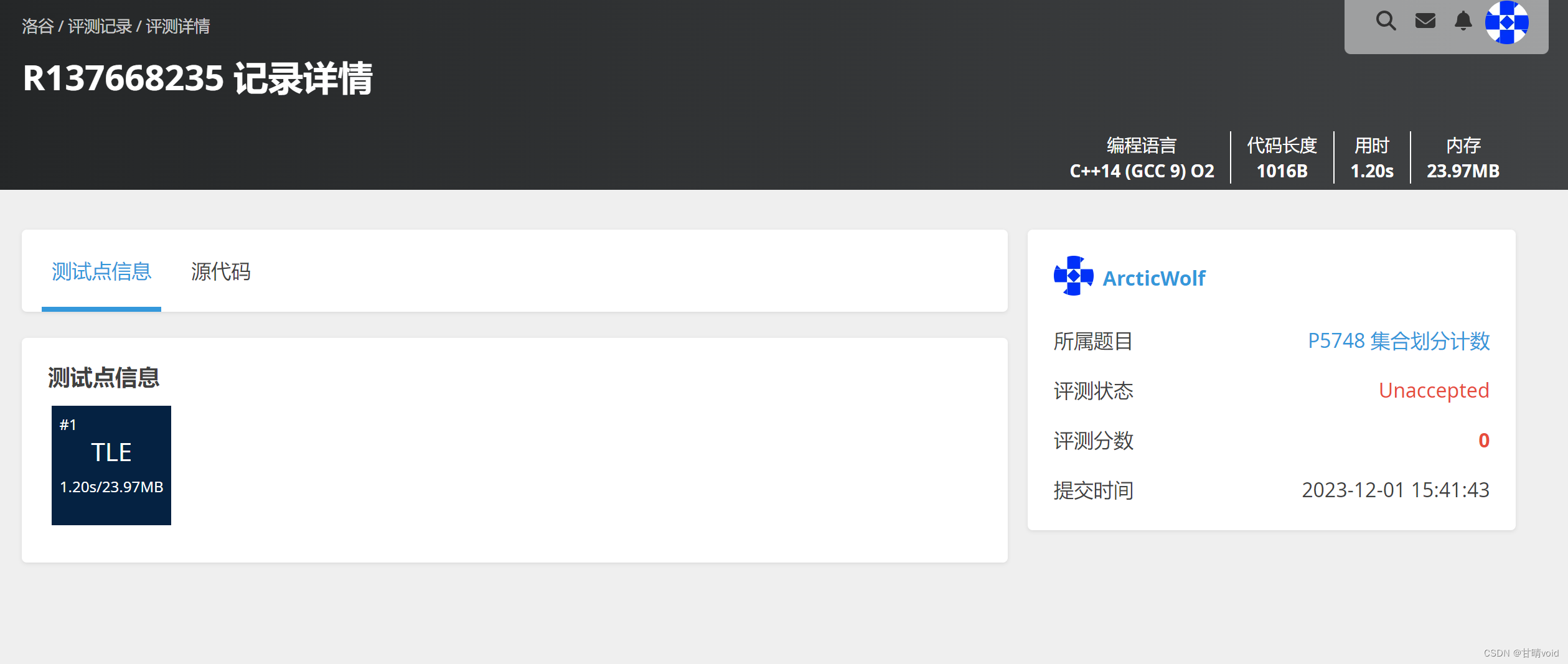
时间消耗太久了,不可接受。
算法分析
时间复杂度O(n^3)
空间复杂度O(n^2)
算法3(贝尔三角形):
想法

为什么贝尔三角形可以解决这个计算问题:

代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100001;
const int mod = 998244353;
long long int bell[maxn], T[maxn];
void Bell(int n, int mod) // 求前n项Bell数
{
bell[0] = bell[1] = 1;
T[0] = 1;
T[1] = 2;
for (int i = 2; i <= n; i++)
{
T[i - 1] = bell[i - 1];
for (int j = i - 2; j >= 0; j--) // 滚动数组
T[j] = (T[j] + T[j + 1]) % mod;
bell[i] = T[0];
}
}
int main()
{
int n, t;
scanf("%d", &t);
Bell(maxn, mod);
for (int i = 0; i < t; i++)
{
scanf("%d", &n);
printf("%lld\n", bell[n]);
}
// for (int i = 0; i < 100; i++) printf("%d%c", bell[i], (i + 1) % 13 == 0 ? '\n' : ' ');
}
验证
较小的数据是可以通过的,
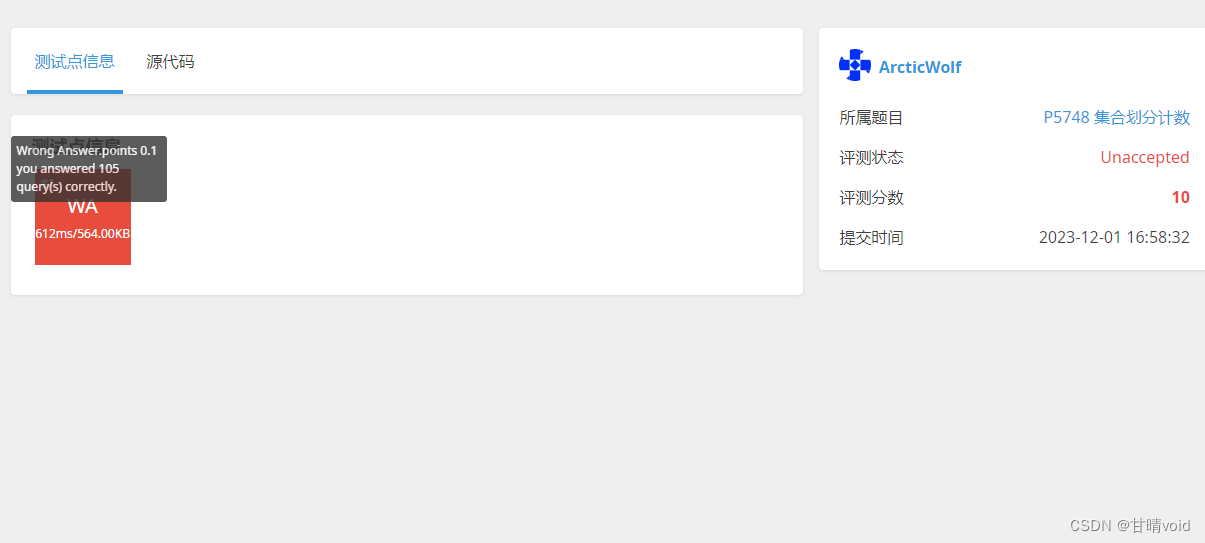
但是对于较大的数据,仍然未通过评测,显示TLE,O(n^2)的时间复杂度应该是没法通过评测的。
算法分析
时间复杂度应该是O(n^2)
空间复杂度O(n^2)
继续深入
对于一道按点得分的题而言,它的数据点是所有数据点。
洛谷的题解涉及到了FFT(快速傅里叶变换),将时间复杂度降到O(nlogn)之后,就可以通过。但是对于有限的课程实验时间,再结合自身能力而言,我决定暂时做到这里了。这是一个遗憾,后续如果有时间我会继续研究。
实验感悟
对于有一些数论的知识,没有能够掌握,这是一个遗憾。如果有足够的时间,还是要多理解多掌握一些。