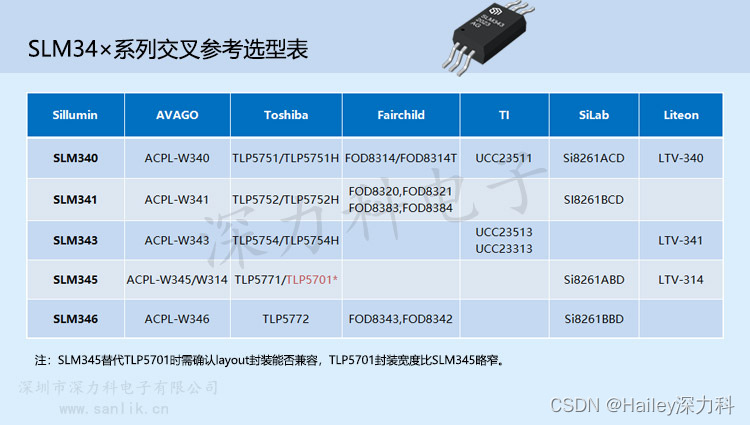
Xor Tree

传送门

题面翻译

给定你一个非负整数序列 $a$，保证其中每个数两两不同。
对于每个 $a_i$，它会向 $j\ne i$ 且 $a_i\oplus a_j$（$\oplus$ 代表异或）最小的 $a_j$ 连双向边。
如果 $a_j$ 也向 $a_i$ 连了边，只算一条边。现在要让你删去序列中的一些数，使得最后形成的图是一颗树，输出最少需要删除几个数。

Translated by 试试事实上吗.

题目描述

For a given sequence of distinct non-negative integers $(b_1,b_2,\dots ,b_k)$ we determine if it is good in the following way:

• Consider a graph on $k$ nodes, with numbers from $b_1$ to $b_k$ written on them.
• For every $i$ from $1$ to $k$ : find such $j$ ( $1\le j\le k$ , $j\ne i$ ), for which $(b_i\oplus b_j)$ is the smallest among all such $j$ , where $\oplus$ denotes the operation of bitwise XOR (https://en.wikipedia.org/wiki/Bitwise_operation#XOR). Next, draw an undirected edge between vertices with numbers $b_i$ and $b_j$ in this graph.
• We say that the sequence is good if and only if the resulting graph forms a tree (is connected and doesn’t have any simple cycles).

It is possible that for some numbers $b_i$ and $b_j$ , you will try to add the edge between them twice. Nevertheless, you will add this edge only once.

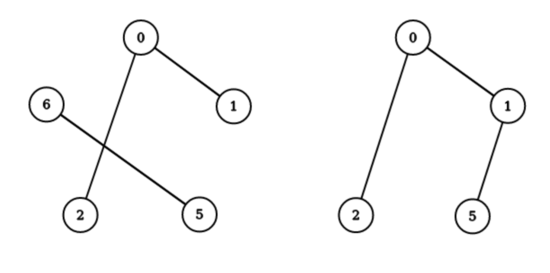
You can find an example below (the picture corresponding to the first test case).

Sequence $(0,1,5,2,6)$ is not good as we cannot reach $1$ from $5$ .

However, sequence $(0,1,5,2)$ is good.

You are given a sequence $(a_1,a_2,\dots ,a_n)$ of distinct non-negative integers. You would like to remove some of the elements (possibly none) to make the remaining sequence good. What is the minimum possible number of removals required to achieve this goal?

It can be shown that for any sequence, we can remove some number of elements, leaving at least $2$ , so that the remaining sequence is good.

输入格式

The first line contains a single integer $n$ ( $2\le n\le 200,000$ ) — length of the sequence.

The second line contains $ n $ distinct non-negative integers $a_1,a_2,\dots ,a_n$ ( $0\le a_i\le 10^9$ ) — the elements of the sequence.

输出格式

You should output exactly one integer — the minimum possible number of elements to remove in order to make the remaining sequence good.

样例 #1

样例输入 #1

5
0 1 5 2 6

样例输出 #1

1

样例 #2

样例输入 #2

7
6 9 8 7 3 5 2

样例输出 #2

2

提示

Note that numbers which you remove don’t impact the procedure of telling whether the resulting sequence is good.

It is possible that for some numbers $b_i$ and $b_j$ , you will try to add the edge between them twice. Nevertheless, you will add this edge only once.

$以上来自洛谷$

解题思路

可将问题转换为转化为求最大保留数，令只存在一对 $(i,j)$ 对彼此而言 $a_i\oplus a_j$ 的值都是最小的。

自然想到 Trie 树。（不会 Trie 树？看这里。）把所有数插入进 Trie 树里，递归考虑 Trie 树的一棵子树 $x$，记令子树 $x$ 合法的最大保留数为 $f_x$，子树 $x$ 的左右儿子对应的是二进制意义下的第 $k$ 位。

当子树 $x$ 只存在左或右儿子时，$f_x$ 的值就是左右儿子的值，否则就是 $\max (LeftSon.f,RightSon.f)+1$。因为在第 $k$ 位之前，对应位的值都相同，仅第 $k$ 位不相同，保留左右子树中的一棵，再保留其余子树的一个节点，就能确保当前子树内只存在一对上述的 $(i,j)$。最后答案就是 $n-f_{rt}$。

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int Maxn = 2e5 + 5;
int n, a[Maxn];
int rt, cnt;
int tong[4000005][2];
inline void Inst(int val) {
	int tmp = rt, cur;
	for (int i = 30; i >= 0; i--) {
		cur = val >> i & 1;
		if (!tong[tmp][cur]) {
			cnt += 1;
			tong[tmp][cur] = cnt;
		}
		tmp = tong[tmp][cur];
	}
}
inline int Fac(int tmp) {
	if (!tong[tmp][0] && !tong[tmp][1]) {
		return 1;
	}
	if (!tong[tmp][0]) {
		return Fac(tong[tmp][1]);
	}
	if (!tong[tmp][1]) {
		return Fac(tong[tmp][0]);
	}
	return max(Fac(tong[tmp][0]), Fac(tong[tmp][1])) + 1;
}
inline void work() {
	rt = cnt = 1;
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		Inst(a[i]);
	}
	cout << n - Fac(rt) << endl;
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	work();
	return 0;
}