认知觉醒(九)
专注力——情绪和智慧的交叉地带
第一节 情绪专注:一招提振你的注意力
用元认知来观察自己的注意力是一件很有意思的事情,相信你可以轻易观察到这种现象:身体做着A,脑子却想着B。
- 跑步的时候,手脚在动,脑子却在考虑明后天的安排;
- 吃饭的时候,嘴巴在动,心里却在担忧与他人的关系;
- 睡觉的时候,身体不动,思绪却像瀑布一样倾泻而出……
这些场景司空见惯,俗称分心、开小差,不过你可能根本不觉得这是个问题,甚至还对自己能一心二用而沾沾自喜。然而这种“做A想B”的行为模式却实实在在地影响着我们,使我们在不知不觉中徒生烦恼、渐生愚钝。从某种意义上说,它正是我们烦恼和无能的来源。
“行动”如躯体,“感受”如灵魂
为了看清这一点,我们可以试着分解注意力。回顾任何一件事,我们的注意力其实都可以分为“集中在行动上的”和“集中在感受上的”两部分,比如:
- 跑步时,跑是行动,剩下的是感受;
- 吃饭时,吃是行动,剩下的是感受;
- 睡觉时,睡是行动,剩下的是感受……
起初,行动和感受二者是统一的。
我们会在做一件事情时全身心地感受这件事情,将注意力全部放在和当前事物相关的事情上,所以跑就是跑,吃就是吃,睡就是睡……我们刚开始学习某项技能,或还只是孩童的时候通常都是这样的,那时的我们善于投入,敏于接受,平和无忧,灵性十足。
随着行动越来越熟练,我们在行动上集中的注意力越来越少,分散在其他地方的注意力越来越多,于是我们不再去耐心感受行动。从此,分心代替专注,身心开始分离(见图4-1)。
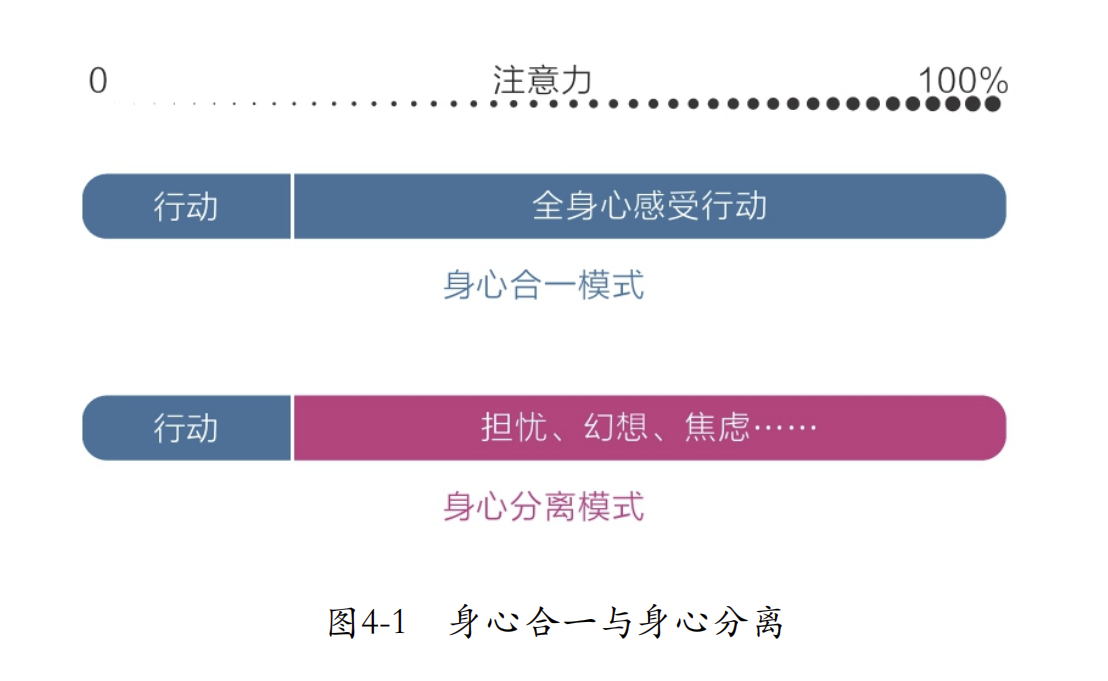
缺少感受的行动,就像失去灵魂的躯壳;缺少感受的人对凡事都心不在焉、视而不见、听而不闻。更准确地说,我们在躯壳内装了一个混乱的灵魂,这个灵魂总是“做A想B”:刷牙的时候走神,走路的时候走神,洗澡的时候走神……无时无刻不在走神。
走神时,行动失去了感知,注意力也因为缺少了感受而无法形成反馈闭环,因此身体和动作开始不自觉地变得麻木或走形。不信的话,你现在就可以感受一下:走神时是不是身体有一部分始终是僵硬的,神情有一部分始终是紧绷的?不过就身心分离模式来说,身体上的影响实属小事,真正严重的是它会对我们的情绪状态和能力提升产生持续的负面影响。
分心走神的原因与危害
分心走神的原因无非两个:一是觉得当下太无聊,所以追求更有意思的事情;二是觉得当下太痛苦,于是追求更舒适的事情。因为身体受困于现实,只好让思想天马行空。
无论我们身在何处、经历着什么,只要现实中稍不如意,我们就可以让思绪上天入地,瞬间逃离困境,享受想象中的舒适和快感。换句话说,就是分心走神的成本太低,而人的天性又是急于求成和避难趋易的,所以在默认情况下,我们都会不自觉地待在精神舒适区内。
可惜“走神一时爽”,事后我们就得承担走神带来的各种损失,其中最大的损失莫过于生命质量变差。因为走神时,我们要么沉浸过去,要么担忧将来,要么幻想不可能实现的情况,走神可以让我们活在任何时候,唯独不能让我们活在当下。
而生命是由当下的一个个片段组成的,身心合一的片段组成的就是幸福专注的高质量人生,身心分离的片段组成的就是分心走神的低质量人生。分心走神还会造成拖延和低效,因为情绪总是滞后于行为,所以人们做事时进入状态往往很慢,需要情绪过渡。
可见,分心走神的本质是逃避,所以,面对困难时,身心分离的人总会不自觉地退回舒适区,而身心合一的人则更容易跳出舒适区,直面困难。
从长远看,一个人专注力的高低可能预示了他今后成就的大小。比尔·盖茨与沃伦·巴菲特第一次相识的时候,盖茨的父亲就分别给他们一人一张卡片,让他们在上面各写一个词,描述究竟是什么成就了自己。结果两个人的答案竟然一模一样,都是专注。
当然,我们也无须为自己的分心走神过于自责,因为从微观来看,分心走神原本就是我们的天性之一。不仅是你,所有人都一样。这背后的原因与我们大脑的记忆机制有关。论记忆能力,人类肯定比不上计算机,无论在容量上还是在精确度上,我们都不具优势,但这并不影响我们提取记忆的速
度,因为人类的大脑使用背景关联记忆的方法,即借助事情的背景或线索等提示信息来让我们想起特定内容,比如我们只根据名字、声音、时间或场景等任意要素就能瞬间想起某人、某事,而计算机则会平等地处理所有信息,每次提取信息都要从数据库中挨个搜索一遍。背景关联记忆的方式可以极大地降低大脑能耗,弥补大脑神经元处理速度的不足。
然而进化是把双刃剑,背景关联记忆的一个副作用就是:我们感观所听到、看到、摸到、尝到、嗅到的任何信息,都会引出一些其他记忆内容,又因为感观受潜意识控制,而潜意识永不消失,所以只要我们醒着,这种分心走神随时都可能发生。这也是我们需要锻炼元认知的原因,因为成长就是克服天性的过程,我们必须用觉知力和自控力去约束天性,否则就会被潜意识左右而不自知。
收回感受,回归当下
如果一个人从小就养成了全情投入和界限清晰的专注习惯,那他不仅能获得智力上的聪慧,也能获得情绪上的平和。经过长期的强化,他就能与普通人形成巨大差距,毕竟绝大多数人意识不到注意力分为行动和感受两个部分。如果我们能早点知道这个原理并主动运用、修正,或许命运轨迹和生活质量都会有所不同。不过现在知道也为时不晚,因为只要一招即可扭转局面:让感受回归行动。
跑步时,把感受收回来,悉心体会抬腿摆臂、呼吸吐纳和迎面的微风;睡觉时,把感受收回来,悉心感受身体的紧张与松弛;吃饭时,把感受收回来,感受每一口饭菜的香甜,体会味觉从有到无的整个过程,不要第一口还没吃完就急着往嘴里塞第二口饭菜。
身体感受永远是进入当下状态的最好媒介,而感受事物消失的过程更是一种很好的专注力训练。它提示我们,身心合一的要领不仅是专注于当下,更是享受当下,而这种享受必将使我们更从容,不慌张。
慢慢练习收回感受,让注意力回到当下,我们的烦恼就会慢慢减少,精力就会更加旺盛,情绪就会更加平和,身体就会更加柔软,感知就会更加灵敏,思考就会更加深入……这个习惯涉及生活的方方面面,改变它就相当于改变了自己的底层行为模式,其力量不可小觑。
最后再讲一个故事,你可能早就听过,不过有了今天的思考,相信你能很快明白其中的深意。
一位行者问老和尚:“您得道前在做什么?”
老和尚说:“砍柴、担水、做饭。”
行者问:“那得道后呢?”
老和尚说:“砍柴、担水、做饭。”
行者又问:“那何谓得道?”
老和尚说:“得道前,砍柴时惦记着挑水,挑水时惦记着做饭;得道后,砍柴即砍柴,担水即担水,做饭即做饭。”
本文摘自:《认知觉醒 : 开启自我改变的原动力》作者:周岭




![街机模拟游戏逆向工程(HACKROM)教程:[0]工具](https://img-blog.csdnimg.cn/direct/95d94f5229324ddfa99495fa80a0dca8.png)