一、是什么

在计算机科学中，二分查找算法，也称折半搜索算法，是一种在有序数组中查找某一特定元素的搜索算法

想要应用二分查找法，则这一堆数应有如下特性：

• 存储在数组中
• 有序排序

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束

如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较

如果在某一步骤数组为空，则代表找不到

这种搜索算法每一次比较都使搜索范围缩小一半

如下图所示：

相比普通的顺序查找，除了数据量很少的情况下，二分查找会比顺序查找更快，区别如下所示：

二、如何实现

基于二分查找的实现，如果数据是有序的，并且不存在重复项，实现代码如下：

function BinarySearch(arr, target) {
    if (arr.length <= 1) return -1
    // 低位下标
    let lowIndex = 0
    // 高位下标
    let highIndex = arr.length - 1

    while (lowIndex <= highIndex) {
        // 中间下标
        const midIndex = Math.floor((lowIndex + highIndex) / 2)
        if (target < arr[midIndex]) {
            highIndex = midIndex - 1
        } else if (target > arr[midIndex]) {
            lowIndex = midIndex + 1
        } else {
            // target === arr[midIndex]
            return midIndex
        }
    }
    return -1
}

如果数组中存在重复项，而我们需要找出第一个制定的值，实现则如下：

function BinarySearchFirst(arr, target) {
    if (arr.length <= 1) return -1
    // 低位下标
    let lowIndex = 0
    // 高位下标
    let highIndex = arr.length - 1

    while (lowIndex <= highIndex) {
        // 中间下标
        const midIndex = Math.floor((lowIndex + highIndex) / 2)
        if (target < arr[midIndex]) {
            highIndex = midIndex - 1
        } else if (target > arr[midIndex]) {
            lowIndex = midIndex + 1
        } else {
            // 当 target 与 arr[midIndex] 相等的时候，如果 midIndex 为0或者前一个数比 target 小那么就找到了第一个等于给定值的元素，直接返回
            if (midIndex === 0 || arr[midIndex - 1] < target) return midIndex
            // 否则高位下标为中间下标减1，继续查找
            highIndex = midIndex - 1
        }
    }
    return -1
}

实际上，除了有序的数组可以使用，还有一种特殊的数组可以应用，那就是轮转后的有序数组

有序数组即一个有序数字以某一个数为轴，将其之前的所有数都轮转到数组的末尾所得

例如，[4, 5, 6, 7, 0, 1, 2]就是一个轮转后的有序数组

该数组的特性是存在一个分界点用来分界两个有序数组，如下：

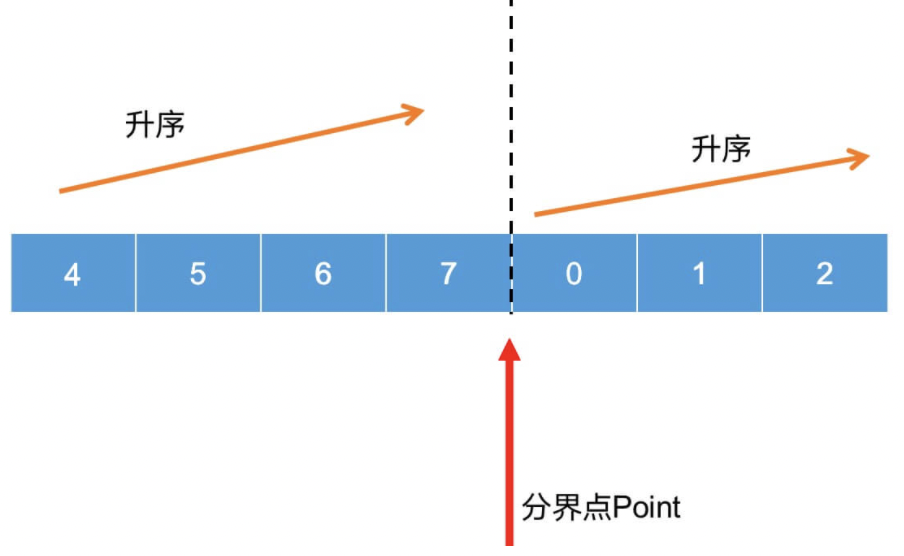
分界点有如下特性：

• 分界点元素 >= 第一个元素
• 分界点元素 < 第一个元素

代码实现如下：

function search (nums, target) {
  // 如果为空或者是空数组的情况
  if (nums == null || !nums.length) {
    return -1;
  }
  // 搜索区间是前闭后闭
  let begin = 0,
    end = nums.length - 1;
  while (begin <= end) {
    // 下面这样写是考虑大数情况下避免溢出
    let mid = begin + ((end - begin) >> 1);
    if (nums[mid] == target) {
      return mid;
    }
    // 如果左边是有序的
    if (nums[begin] <= nums[mid]) {
      //同时target在[ nums[begin],nums[mid] ]中，那么就在这段有序区间查找
      if (nums[begin] <= target && target <= nums[mid]) {
        end = mid - 1;
      } else {
        //否则去反方向查找
        begin = mid + 1;
      }
      //如果右侧是有序的
    } else {
      //同时target在[ nums[mid],nums[end] ]中，那么就在这段有序区间查找
      if (nums[mid] <= target && target <= nums[end]) {
        begin = mid + 1;
      } else {
        end = mid - 1;
      }
    }
  }
  return -1;
};

对比普通的二分查找法，为了确定目标数会落在二分后的哪个部分，我们需要更多的判定条件

三、应用场景

二分查找法的O(logn)让它成为十分高效的算法。不过它的缺陷却也是比较明显，就在它的限定之上：

• 有序：我们很难保证我们的数组都是有序的
• 数组：数组读取效率是O(1)，可是它的插入和删除某个元素的效率却是O(n)，并且数组的存储是需要连续的内存空间，不适合大数据的情况

关于二分查找的应用场景，主要如下：

• 不适合数据量太小的数列；数列太小，直接顺序遍历说不定更快，也更简单
• 每次元素与元素的比较是比较耗时的，这个比较操作耗时占整个遍历算法时间的大部分，那么使用二分查找就能有效减少元素比较的次数
• 不适合数据量太大的数列，二分查找作用的数据结构是顺序表，也就是数组，数组是需要连续的内存空间的，系统并不一定有这么大的连续内存空间可以使用

参考文献

• https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%88%86%E6%90%9C%E5%B0%8B%E6%BC%94%E7%AE%97%E6%B3%95#javascript_%E7%89%88%E6%9C%AC
• https://www.cnblogs.com/ider/archive/2012/04/01/binary_search.html

更多前端资源==> GitHub