3.三极管和MOS管
- 基础知识
- 三极管是电流控制型器件
- MOS管是电压控制型器件
- 分类及引脚定义
- 电流导通方向
- 基础应用
- 常用MOS管电平转换电路
- MOS管实现电平转换
- 用MOS管实现的“I2C总线电平转换电路”,实现3.3V电压域与5V电压域间的双向通讯
基础知识
三极管是电流控制型器件
三极管的导通,需要在其b极提供电流,才能使ce导通,流过ce之间的电流与b极电流的关系是Ib*β=Ice,这个β称为三极管的放大倍数,从规格书获取,典型值是100,同一个芯片不同Ib的β也是不同的。
MOS管是电压控制型器件
MOS管的导通,以NMOS为例,需要提供一定的Vgs电压,这个参数在规格书中称为Vgs(th),也就是导通所需要的电压。
分类及引脚定义
从半导体结构上分
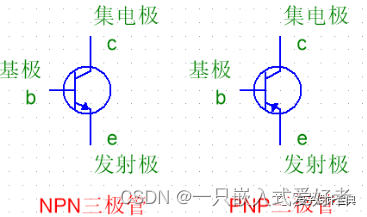
按沟道分
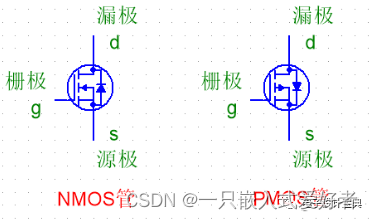
电流导通方向
三极管导通方向,NPN:c→e,PNP:e→c
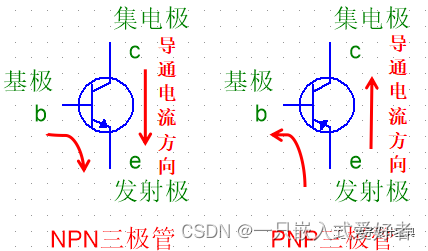
MOS管导通方向
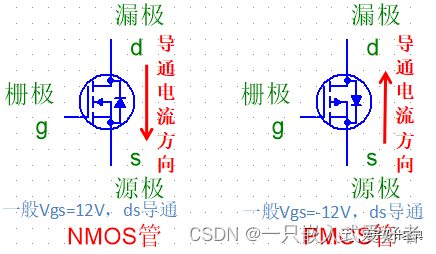
基础应用
NPN三极管和NMOS管
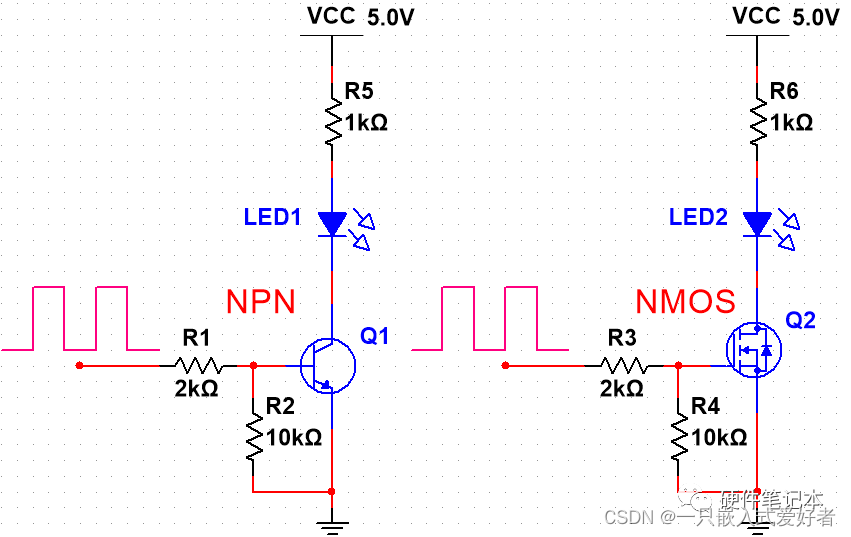
PNP三极管和PMOS管
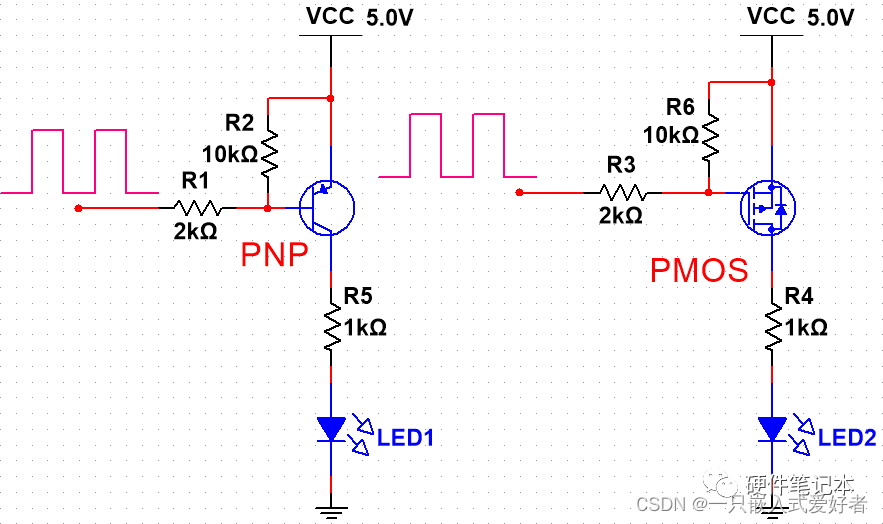
常用MOS管电平转换电路
电平及电源转换电路是硬件设计中的常见电路,用于将一个电平/电源转换为另一个不同电平/电源,确保外设之间可以正常通信和工作。
基于MOS管的电平转换电路基本模型:
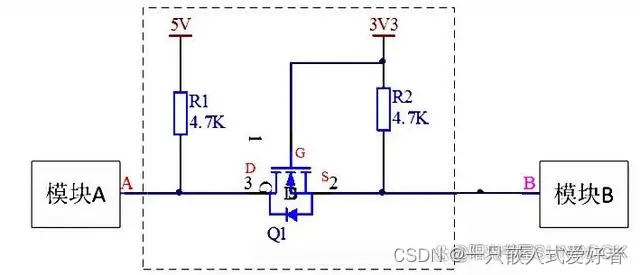
工作原理:
- 从A到B
A为高电平时,B作为输入,此时为高阻态,MOS管关断,B端通过上拉,输出高电平;A为低电平时,MOS管内的体二极管导通,使MOS管的S极被拉低,考虑体二极管的压降一般为0.7V,Vgs=3.3V-0.7V=2.6V,当Vgs=2.6V>Vgs(th),MOS管导通,B端被拉低,输出低电平;(MOS管的导通阈值电压一定要小于2.6V),A为高阻态时,MOS管关断,B端通过上拉,输出高电平。 - 从B到A
B为高电平时,MOS管关断,A端通过上拉,输出高电平;B为低电平时,Vgs=3.3V>Vgs(th),MOS管导通,A端被拉低,输出低电平;B为高阻态时,MOS管关断,A端通过上拉,输出高电平。
MOS管实现电平转换
需求:使用一个NMOS管就实现双向电平转换功能,且输出电平与输入电平极性相同,具体具体电路见下:
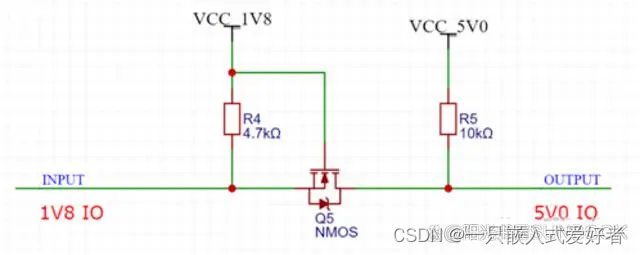
电路分析:
- 当INPUT=0时,NMOS管导通,OUTPUT通过NMOS下拉至GND,此时OUTPUT输出为低电平;
- 当INPUT=1时,NMOS管截止,OUTPUT被R5上拉至VCC_5V0,此时OUTPUT输出为高电平;
- 当OUTPUT=0时,体二极管导通,INPUT为体二极管上压降(约0.7V),可视为INPUT为低电平;
- 当OUTPUT=1时,体二极管和NMOS管均截止,INPOT被R上拉至VCC_1V8,INPIT输出高电平。
用MOS管实现的“I2C总线电平转换电路”,实现3.3V电压域与5V电压域间的双向通讯
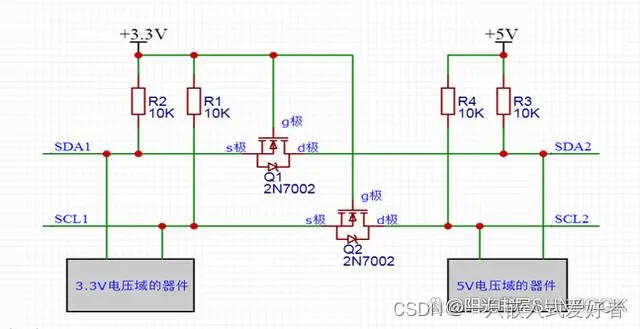
工作原理分析,简化来看,留下I2C的一根线来分析就可以了。
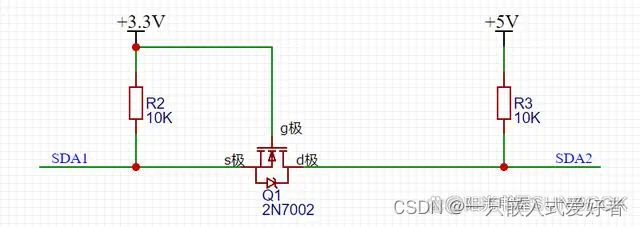
分四种情况:
- 当SDA1输出高电平时:MOS管Q1的Vgs = 0,MOS管关闭,SDA2被电阻R3上拉到5V。
- 当SDA1输出低电平时:MOS管Q1的Vgs = 3.3V,大于导通电压,MOS管导通,SDA2通过MOS管被拉到低电平。
- 当SDA2输出高电平时:MOS管Q1的Vgs不变,MOS维持关闭状态,SDA1被电阻R2上拉到3.3V。
- 当SDA2输出低电平时:MOS管不导通,但是它有体二极管!MOS管里的体二极管把SDA1拉低到低电平,此时Vgs约等于3.3V,MOS管导通,进一步拉低了SDA1的电压。