一、梯度下降法
# 梯度下降不是一种算法,是一种最优化方法
# 上节课讲解的梯度下降的案例 是一个简单的一元二次方程
# 最简单的线性回归:只有一个特征的线性回归,有两个theta
#
二、在多元线性回归中使用梯度下降求解
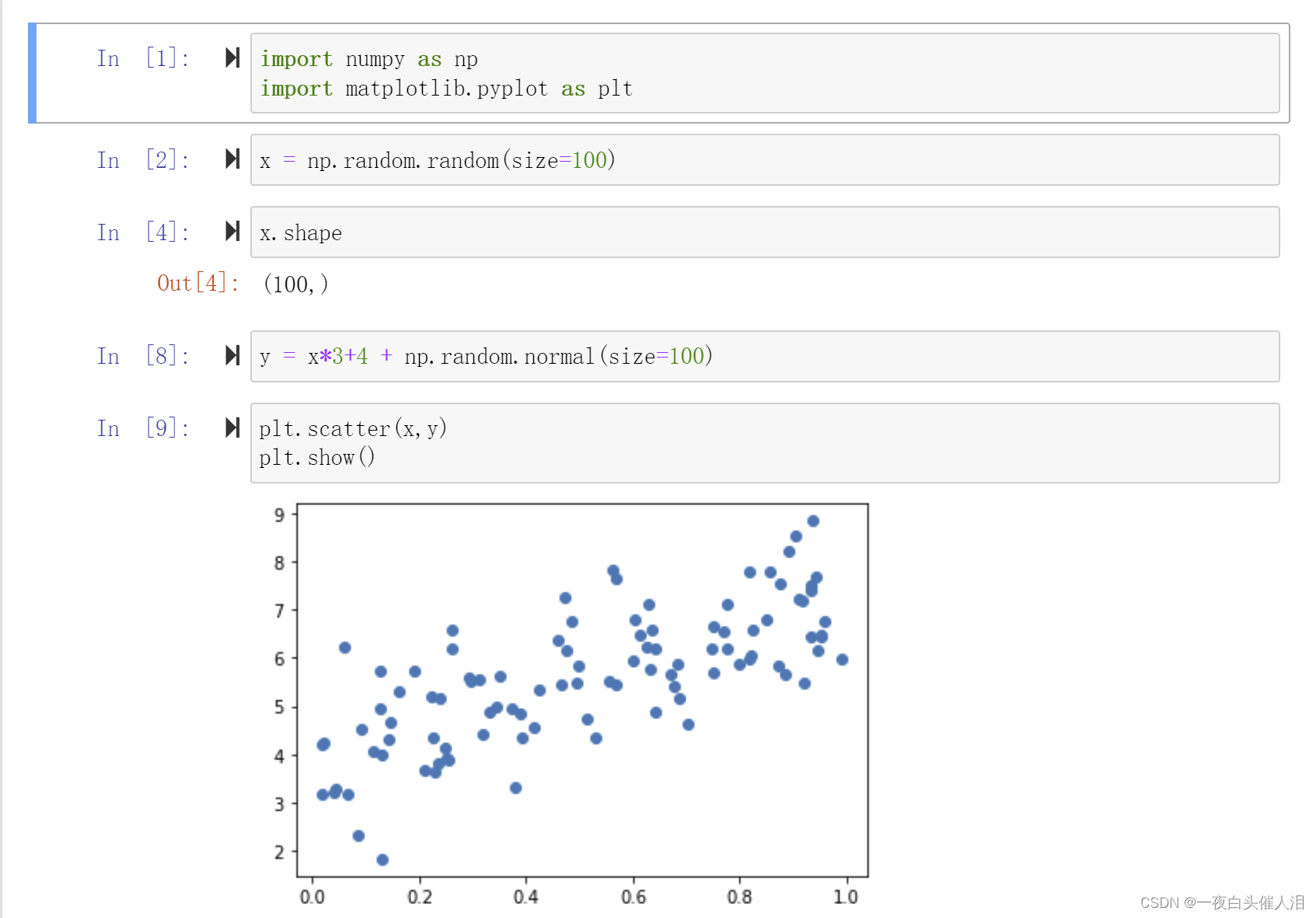
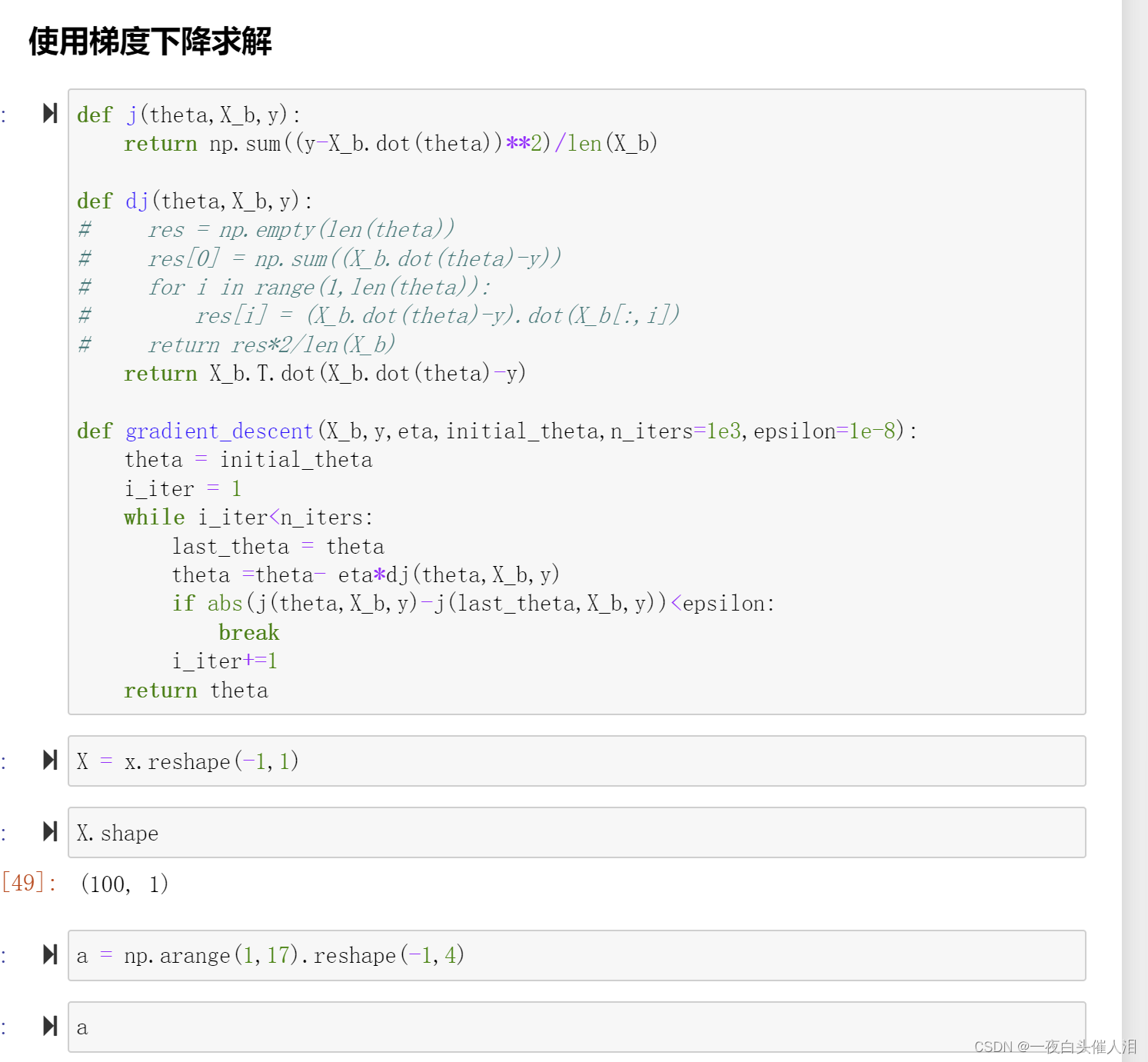

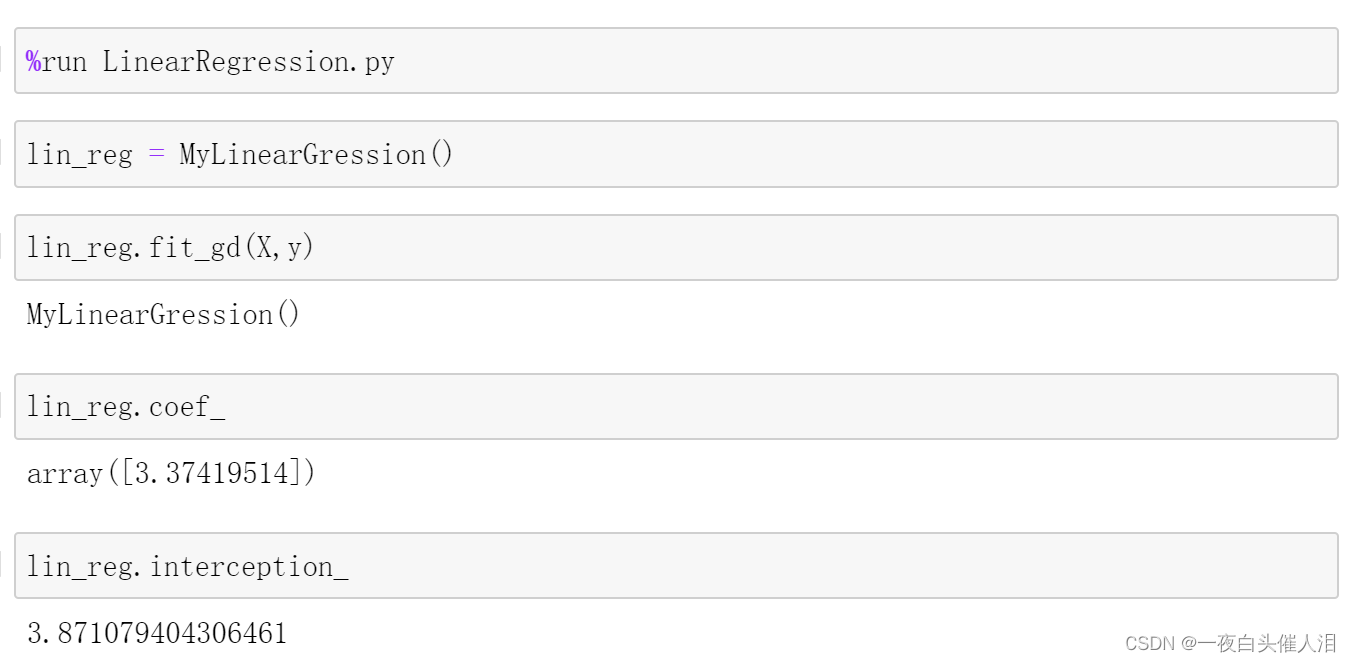
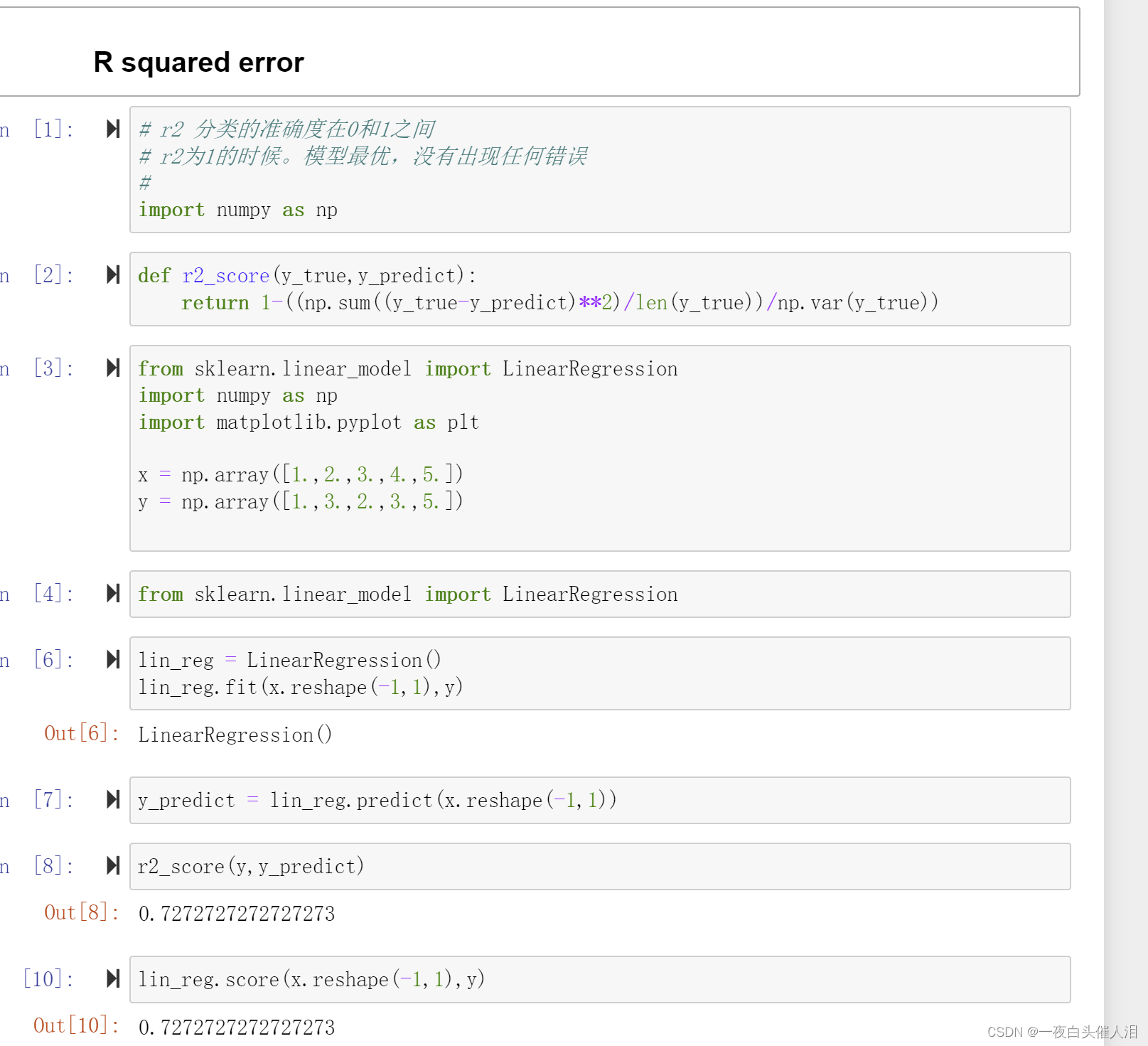
三、### R squared error
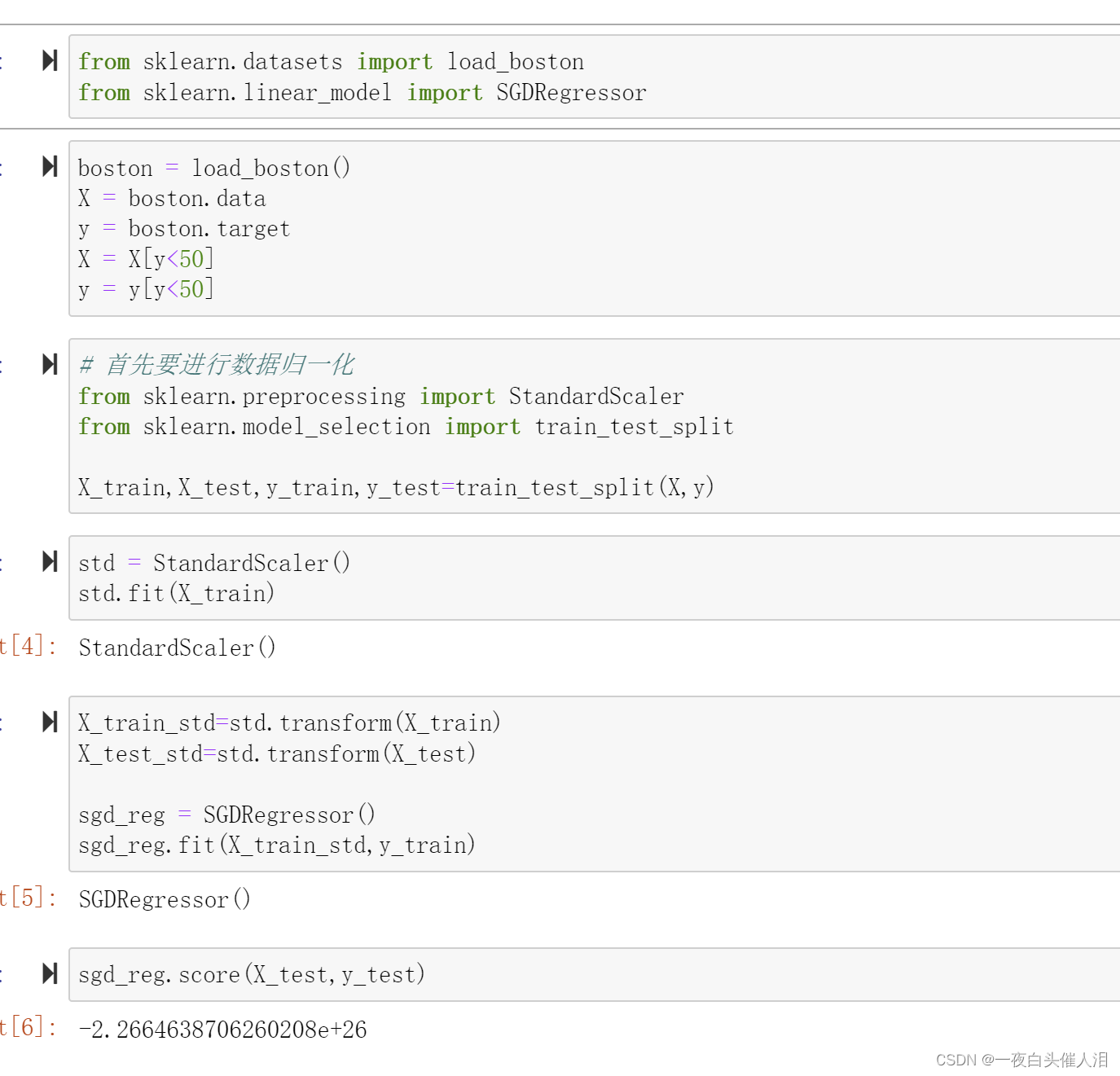
使用真实数据来进行梯度下降的过程
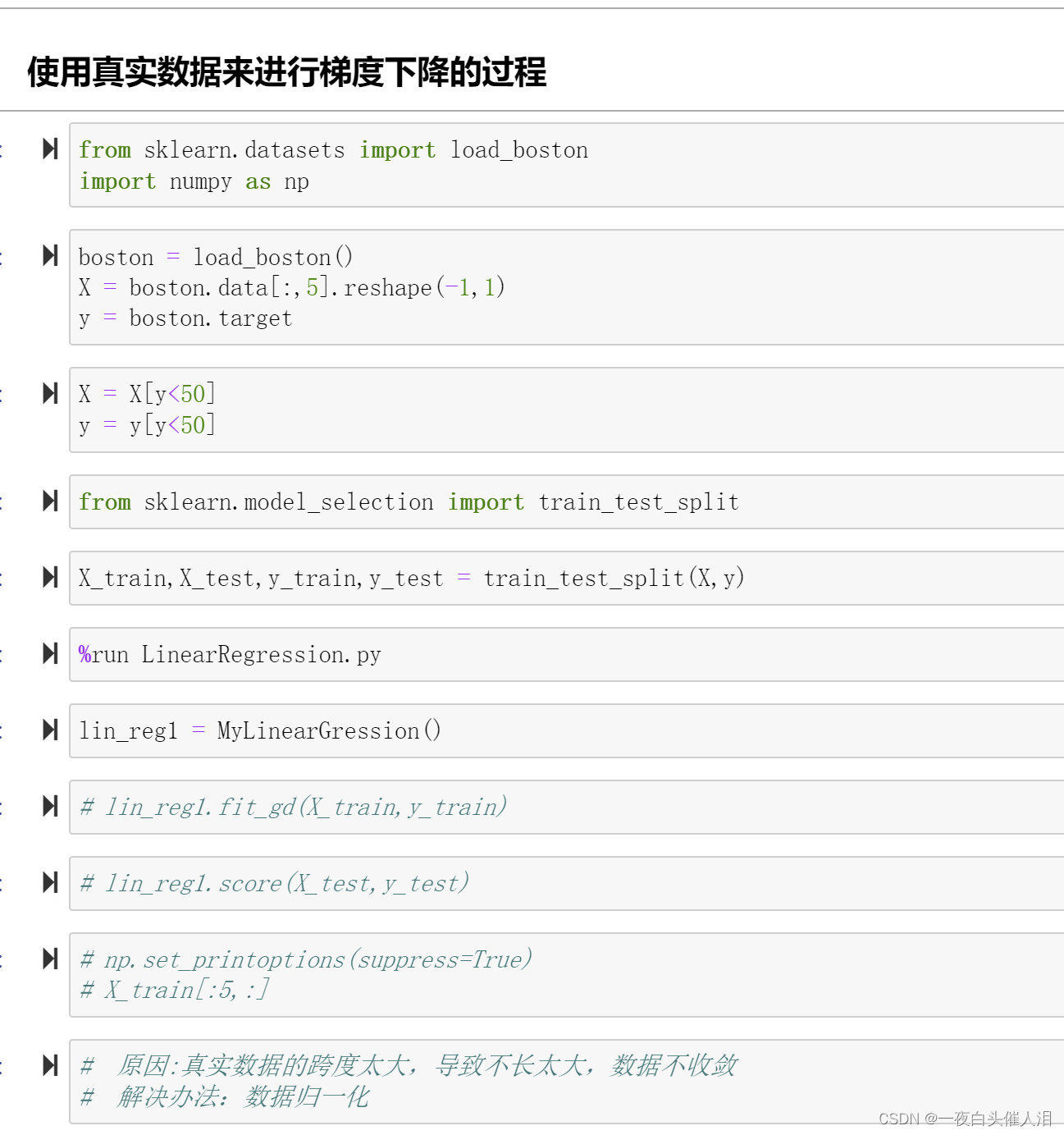
# 如果特征数多,样本数少,梯度下降法占优
# 如果特征数少,样本数多,梯度下降法的效率会比较低
import numpy as np
def r2_score(y_true, y_predict):
return 1 - ((np.sum((y_true - y_predict) ** 2) / len(y_true)) / np.var(y_true))
class MyLinearGression:
def __init__(self):
self._theta = None # theta参数
self.coef_ = None # 系数
self.interception_ = None # 截距
def fit_gd(self, X_train, y, eta=0.01, n_iters=1e3, epsilon=1e-8): # 使用梯度下降的方式来训练数据
def j(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(X_b)
except:
return float('inf')
def dj(theta, X_b, y):
# res = np.empty(len(theta))
# res[0] = np.sum((X_b.dot(theta) - y))
# for i in range(1, len(theta)):
# res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
# return res * 2 / len(X_b)
return X_b.T.dot(X_b.dot(theta) - y)
def gradient_descent(X_b, y, eta, initial_theta, n_iters=1e3, epsilon=1e-8):
theta = initial_theta
i_iter = 1
while i_iter < n_iters:
last_theta = theta
theta = theta - eta * dj(theta, X_b, y)
if abs(j(theta, X_b, y) - j(last_theta, X_b, y)) < epsilon:
break
i_iter += 1
return theta
# eta = 0.01
X_b = np.hstack([np.ones(len(X_train)).reshape(-1, 1), X_train])
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y, eta, initial_theta)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def __repr__(self):
return "MyLinearGression()"
def score(self, X_predict, y_test):
y_predict = self.predict(X_predict)
return r2_score(y_test, y_predict)
def predict(self, X_predict):
X_b = np.hstack([np.ones(len(X_predict)).reshape(-1, 1), X_predict])
return X_b.dot(self._theta)
四、总结
knn算法 线性回归 数据的预处理(标准化) 模型好坏的校验



五 梯度下降法
# 梯度下降不是一个机器学习算法,既不是再做监督学习,也不是在做非监督学习,是一种基于搜索的最优化方法
# 作用:最小化一个损失函数
# 梯度上升法:最大化一个效用函数
# eta叫做学习率,learning rate
# eta的取值影响我们求得最优解的速度
# eta如果取值过小,收敛太慢
# eta取值过大,可能甚至得不到最优解
# eta他是梯度下降法的一个超参数
# 并不是所有的函数都有唯一的极值点
# 线性回归的损失函数具有唯一的最优解
# gradient inscent
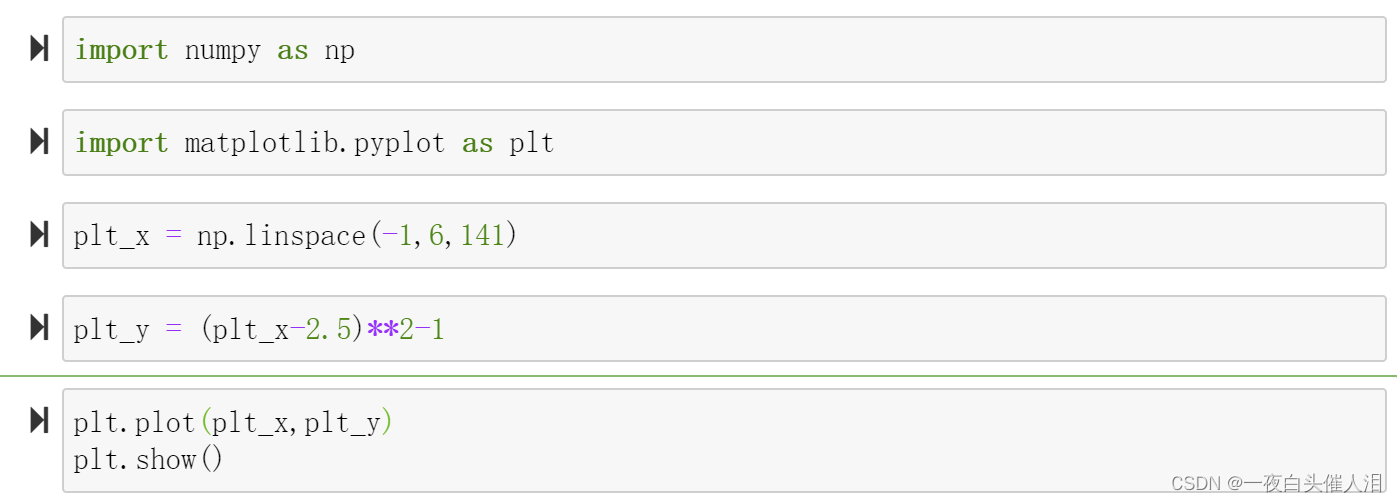
import numpy as np
import matplotlib.pyplot as plt
plt_x = np.linspace(-1,6,141)
plt_y = (plt_x-2.5)**2-1
plt.plot(plt_x,plt_y)
plt.show()
def dj(theta):
return 2*(theta-2.5) # 传入theta,求theta点对应的导数
def j(theta):
return (theta-2.5)**2-1 # 传入theta,获得目标函数的对应值
eta = 0.1
theta =0.0
epsilon = 1e-8
while True:
gradient = dj(theta)
last_theta = theta
theta = theta-gradient*eta
if np.abs(j(theta)-j(last_theta))<epsilon:
break
print(theta)
print(dj(theta))
print(j(theta))
eta = 0.1
theta =0.0
epsilon = 1e-8
theta_history = [theta]
while True:
gradient = dj(theta)
last_theta = theta
theta = theta-gradient*eta
theta_history.append(theta)
if np.abs(j(theta)-j(last_theta))<epsilon:
break
print(theta)
print(dj(theta))
print(j(theta))
len(theta_history)
plt.plot(plt_x,plt_y)
plt.plot(theta_history,[(i-2.5)**2-1 for i in theta_history],color='r',marker='+')
plt.show()
def gradient_descent(eta,initial_theta,n_iters=1e3,epsilon = 1e-8):
theta = initial_theta
theta_history = [initial_theta]
i_iter = 1
def dj(theta):
try:
return 2*(theta-2.5) # 传入theta,求theta点对应的导数
except:
return float('inf')
def j(theta):
return (theta-2.5)**2-1 # 传入theta,获得目标函数的对应值
while i_iter<=n_iters:
gradient = dj(theta)
last_theta = theta
theta = theta-gradient*eta
theta_history.append(theta)
if np.abs(j(theta)-j(last_theta))<epsilon:
break
i_iter+=1
return theta_history
def plot_gradient(theta_history):
plt.plot(plt_x,plt_y)
plt.plot(theta_history,[(i-2.5)**2-1 for i in theta_history],color='r',marker='+')
plt.show()
eta = 0.1
theta =0.0
plot_gradient(gradient_descent(eta,theta))
eta = 0.01 # eta越小,迭代次数越多,耗时越久
theta =0.0
theta_history = gradient_descent(eta,theta)
plot_gradient(theta_history)
len(theta_history)
eta = 0.8 # 说明eta的取值不是特别准确,也可以得到正确的结果
theta =0.0
plot_gradient(gradient_descent(eta,theta))
eta = 1.1 # 说明eta取值太大
theta =0.0
plot_gradient(gradient_descent(eta,theta))
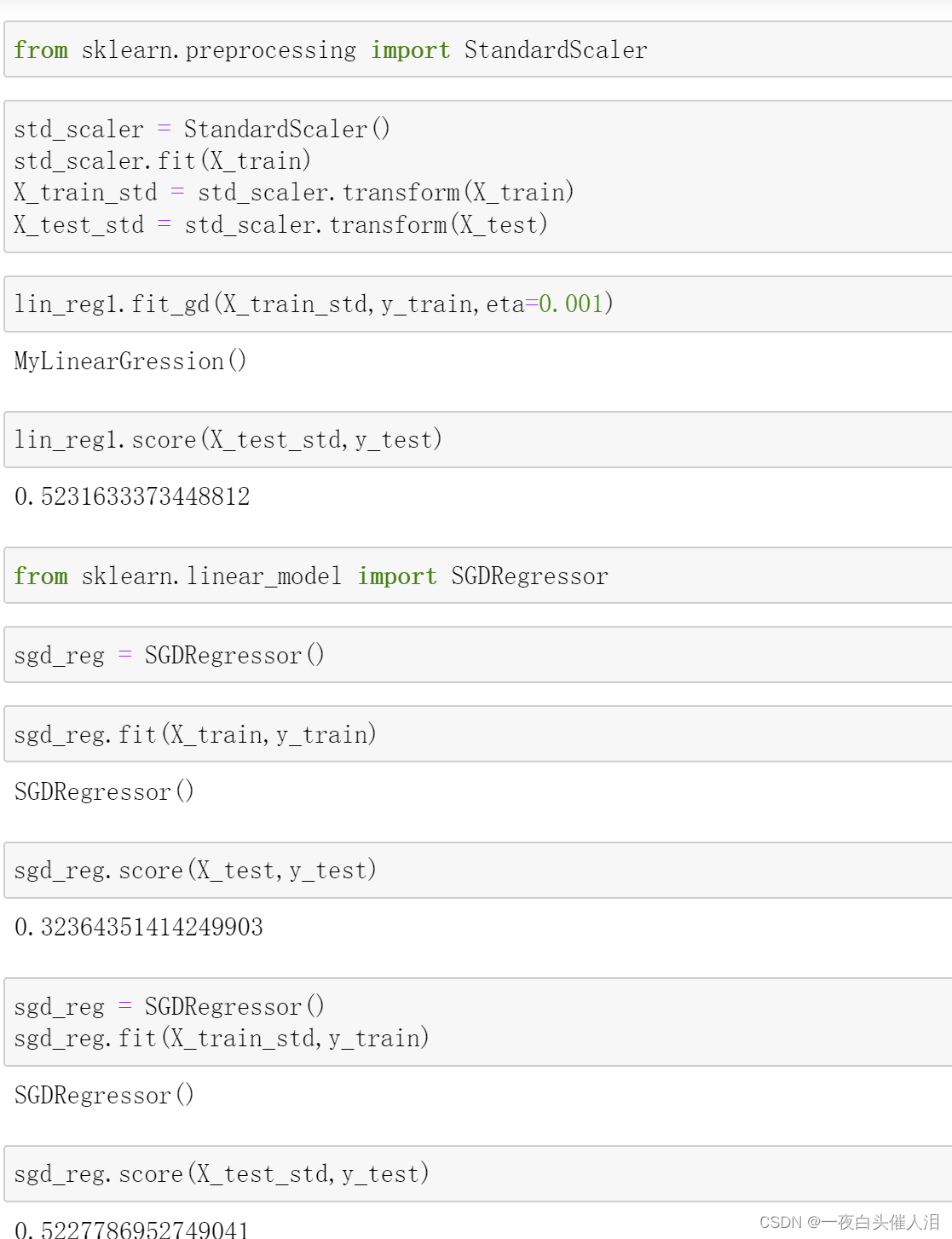
六、sklearn中使用梯度下降法