蓝桥杯
我的AcWing
题目及图片来自蓝桥杯C++ AB组辅导课
数论(下)
蓝桥杯省赛中考的数论不是很多,这里讲几个蓝桥杯常考的知识点。
约数个数定理
我们如何去求一个数的约数个数呢?
N N N分解质因数的结果: N = P 1 α 1 × P 2 α 2 × . . . × P k α k N=P_{1}^{α_{1}}×P_{2}^{α_{2}}×...×P_{k}^{α_{k}} N=P1α1×P2α2×...×Pkαk
约数个数是: ( α 1 + 1 ) ( α 2 + 1 ) . . . ( α k + 1 ) (α_{1}+1)(α_{2}+1)...(α_{k}+1) (α1+1)(α2+1)...(αk+1)
假设 N N N的一个约数 d = P 1 β 1 × P 2 β 2 × . . . × P k β k ( 0 ≤ β i ≤ α i ) d=P_{1}^{β_{1}}×P_{2}^{β_{2}}×...×P_{k}^{β_{k}}(0 \leq β_{i}\leq α_{i}) d=P1β1×P2β2×...×Pkβk(0≤βi≤αi),每一个约数都可以表示为这样的形式,这种约数的个数也就等于 k k k 元组的个数: ( β 1 , β 2 . . . β k ) (β_{1},β_{2}...β_{k}) (β1,β2...βk),这 k k k 元组有多少种选法: ( α 1 + 1 ) ⋅ ( α 2 + 1 ) ⋅ ( α k + 1 ) (α_{1}+1)·(α_{2}+1)·(α_{k}+1) (α1+1)⋅(α2+1)⋅(αk+1)
约数和定理
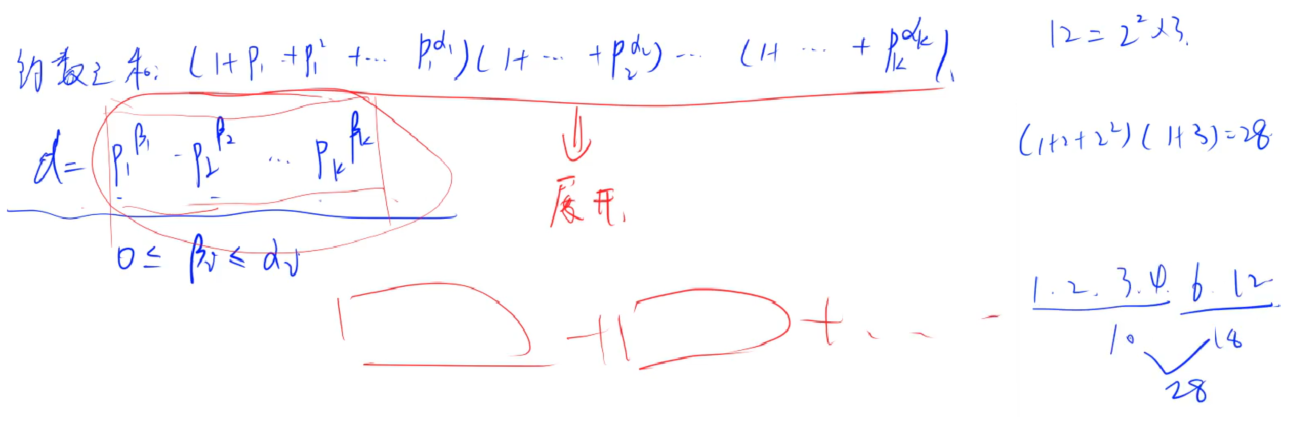
公式: ( 1 + P 1 + P 1 2 + . . + P 1 α 1 ) ( 1 + P 2 + P 2 2 + . . + P 2 α 2 ) . . . ( 1 + P k + P k 2 + . . + P k α k ) (1+P_{1}+P_{1}^2+..+P_{1}^{α_{1}})(1+P_{2}+P_{2}^2+..+P_{2}^{α_{2}})...(1+P_{k}+P_{k}^2+..+P_{k}^{α_{k}}) (1+P1+P12+..+P1α1)(1+P2+P22+..+P2α2)...(1+Pk+Pk2+..+Pkαk)
这个公式展开了就是上面定理的约数 d = P 1 β 1 × P 2 β 2 × . . . × P k β k ( 0 ≤ β i ≤ α i ) d=P_{1}^{β_{1}}×P_{2}^{β_{2}}×...×P_{k}^{β_{k}}(0 \leq β_{i}\leq α_{i}) d=P1β1×P2β2×...×Pkβk(0≤βi≤αi) 之和。
例题
AcWing 1296. 聪明的燕姿
约数个数定理
约数和定理
给我们一个 S S S,问我们有多少个正整数满足它的所有正约数之和等于 S S S。
S S S 满足约数和定理: S = ( 1 + P 1 + P 1 2 + . . + P 1 α 1 ) ( 1 + P 2 + P 2 2 + . . + P 2 α 2 ) . . . ( 1 + P k + P k 2 + . . + P k α k ) S=(1+P_{1}+P_{1}^2+..+P_{1}^{α_{1}})(1+P_{2}+P_{2}^2+..+P_{2}^{α_{2}})...(1+P_{k}+P_{k}^2+..+P_{k}^{α_{k}}) S=(1+P1+P12+..+P1α1)(1+P2+P22+..+P2α2)...(1+Pk+Pk2+..+Pkαk)
因为方案数非常少,我们可以用暴搜dfs求解。
这题太难理解啦,之后的题也没有做了。