力扣热题 100

news2025/1/24 8:26:30

文章目录

    • 哈希
    • 双指针
    • 滑动窗口
    • 子串
    • 普通数组
    • 矩阵
    • 链表
    • 二叉树
    • 图论
    • 回溯
    • 二分查找
    • 栈
    • 堆
    • 贪心算法
    • 动态规划
    • 多维动态规划
    • 技巧

哈希

双指针

  1. 移动零
class Solution {
    public void moveZeroes(int[] nums) {
        int k = 0;
        for(int i = 0;i < nums.length; i++){
            if(nums[i] != 0) {
                nums[k] = nums[i];
                k++;
            }
        }
        for (int i = k; i < nums.length; i++) {
            nums[i] = 0;
        }
    }
}

class Solution {
    public void moveZeroes(int[] nums) {
        int k = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                int temp = nums[i];
                nums[i] = nums[k];
                nums[k] = temp;
                k++;
            }
        }
    }
}
  1. 盛最多水的容器
class Solution {
    public int maxArea(int[] height) {
        int left = 0, right = height.length - 1;
        int ans = 0;
        while (left < right) {
            int area = Math.min(height[left], height[right]) * (right - left);
            ans = Math.max(ans, area);
            if (height[left] <= height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return ans;
    }
}
  1. 接雨水
class Solution {
    public int trap(int[] height) {
        int left = 0, right = height.length - 1;
        int leftMax = 0, rightMax = 0;

        int ans = 0;
        while (left < right) {
            leftMax = Math.max(leftMax, height[left]);
            rightMax = Math.max(rightMax, height[right]);
            if (height[left] < height[right]) {
                ans += leftMax - height[left];
                left++;
            } else {
                ans += rightMax - height[right];
                right--;
            }
        }
        return ans;
    }
}

滑动窗口

子串

普通数组

矩阵

链表

二叉树

  1. 二叉树的中序遍历
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> reusltList = new ArrayList<>();
        inorderVisited(root, reusltList);
        return  reusltList;
    }

    private void inorderVisited(TreeNode root, List<Integer> reusltList) {
        if (root == null) {
            return;
        }
        inorderVisited(root.left, reusltList);
        reusltList.add(root.val);
        inorderVisited(root.right, reusltList);
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        
        Deque<TreeNode> stack = new LinkedList<>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            ans.add(root.val);
            root = root.right;
        }
        return ans;
    }
}
  1. 二叉树的最大深度
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
 //深度优先遍历
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
//广度优先遍历
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int ans = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size > 0) {
                TreeNode node = queue.poll();
                if (node.left != null)
                    queue.offer(node.left);
                if (node.right != null)
                    queue.offer(node.right);
                size--;
            }
            ans++;
        }
        return ans;
    }
}
  1. 翻转二叉树
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        TreeNode temp = root.right;
        root.right = root.left;
        root.left = temp;

        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size > 0) {
                TreeNode node = queue.poll();
                TreeNode temp = node.left;
                node.left = node.right;
                node.right = temp;

                if (node.left != null)
                    queue.offer(node.left);
                if (node.right != null)
                    queue.offer(node.right);
                size--;
            }
        }
        return root;
    }
}
  1. 对称二叉树
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null) {
            return true;
        }
        return dfs(root.left, root.right);
    }

    boolean dfs(TreeNode left, TreeNode right) {
        if(left == null && right == null) return true;

        if(left == null || right == null) return false;

        if(left.val != right.val) return false;

        return dfs(left.left, right.right) && dfs(left.right, right.left);
    }
}
  1. 二叉树的直径
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    int ans = 0;

    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        return ans;
    }

    public int depth(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int left = depth(node.left);
        int right = depth(node.right);
        ans = Math.max(left + right, ans);

        return Math.max(left, right) + 1;
    }
}
  1. 二叉树的层序遍历
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> resultList = new ArrayList<>();

        if (root == null) {
            return resultList;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> temp = new ArrayList<>();
            while (size > 0) {
                TreeNode node = queue.poll();
                temp.add(node.val);
                if (node.left != null)
                    queue.offer(node.left);
                if (node.right != null)
                    queue.offer(node.right);
                size--;
            }
            resultList.add(temp);
        }
        return resultList;
    }
}
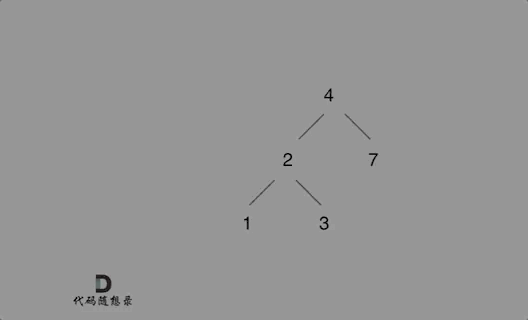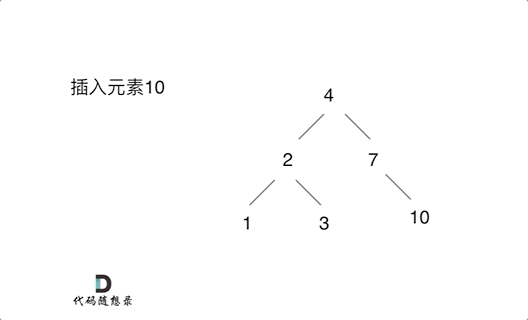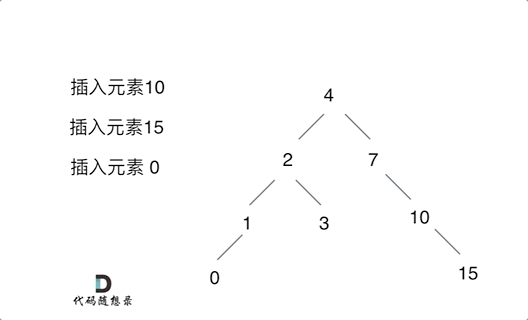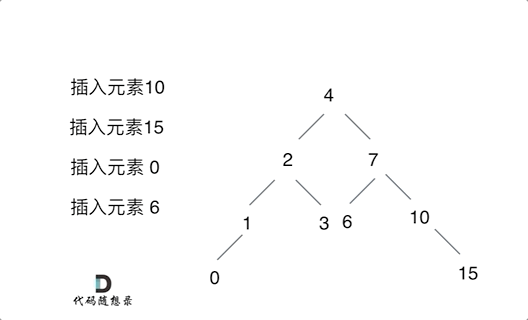
  1. 将有序数组转换为二叉搜索树
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return helper(nums, 0, nums.length - 1);
    }

    TreeNode helper(int[] nums, int left, int right) {
        if (left > right) {
            return null;
        }

        int mid = (left + right) / 2;

        TreeNode root = new TreeNode(nums[mid]);
        root.left = helper(nums, left, mid - 1);
        root.right = helper(nums, mid + 1, right);
        return root;
    }
}
  1. 验证二叉搜索树
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 // 中序遍历
class Solution {
    long pre = Long.MIN_VALUE;

    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        if (!isValidBST(root.left)) {
            return false;
        }
        if (root.val <= pre) {
            return false;
        }
        pre = root.val;
        if (!isValidBST(root.right)) {
            return false;
        }
        return true;
    }

}
  1. 二叉搜索树中第K小的元素
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> list = new ArrayList<>();

    public int kthSmallest(TreeNode root, int k) {
        inOrderVisited(root);
        return list.get(k - 1);
    }

    void inOrderVisited(TreeNode root) {
        if (root == null) {
            return;
        }
        inOrderVisited(root.left);
        list.add(root.val);
        inOrderVisited(root.right);
    }

}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Deque<TreeNode> stack = new LinkedList<>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            k--;
            if (k == 0) break;
            root = root.right;
        }
        return root.val;

    }
}

图论

回溯

二分查找

栈

堆

贪心算法

动态规划

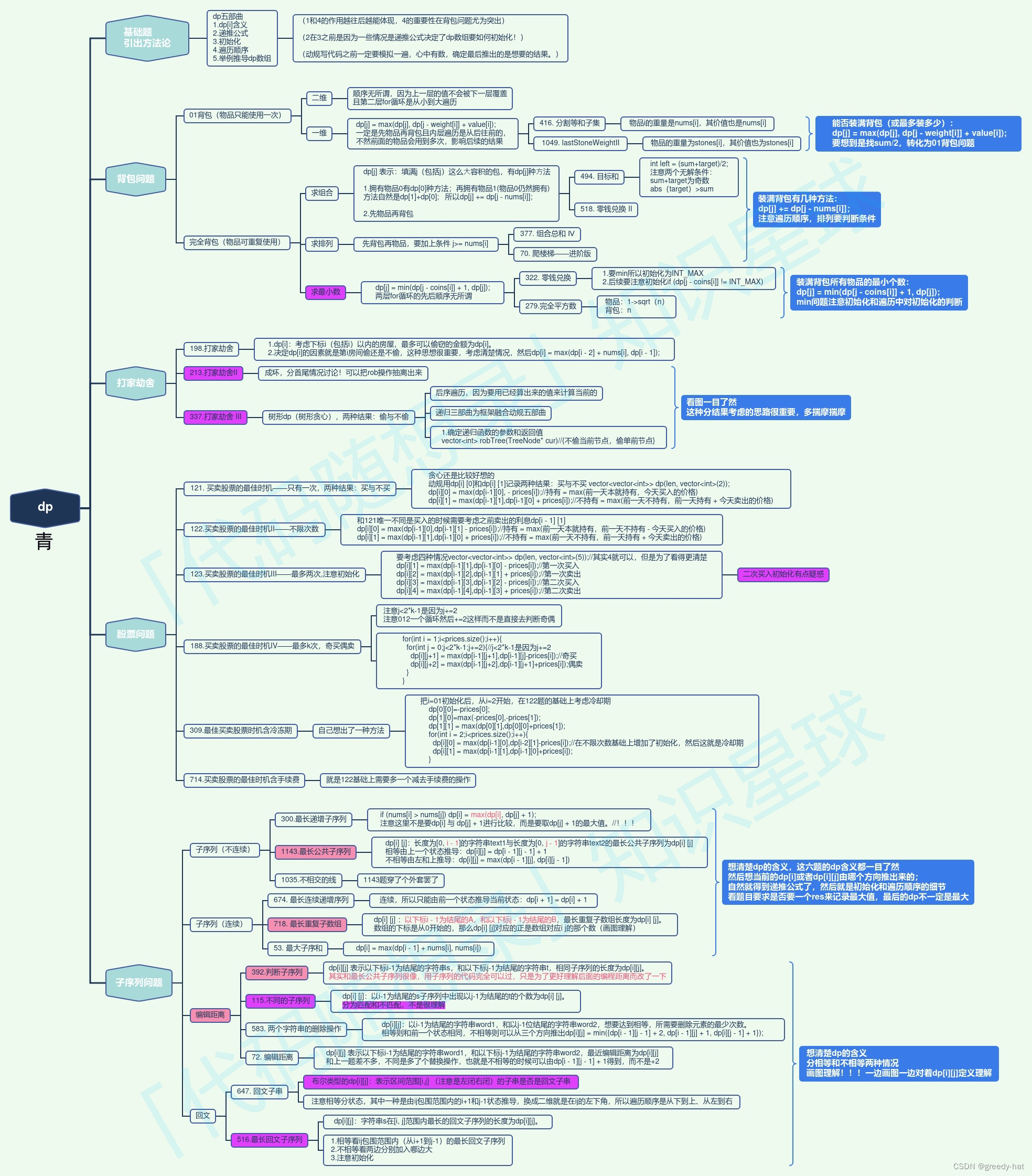
在这里插入图片描述

  1. 爬楼梯
class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2;i <= n; i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
}
  1. 打家劫舍
class Solution {
    public int rob(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }

        int len = nums.length;
        int[] dp = new int[len+1];
        dp[0] = 0;
        dp[1] = nums[0];
        for(int i = 2; i <= len; i++){
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
        }
        return dp[len];
    }
}
  1. 完全平方数
class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        for(int i = 1; i <= n;i++) {
            int minn = Integer.MAX_VALUE;
            for(int j = 1; j * j <= i; j++){
                minn = Math.min(minn, dp[i - j * j]);
            }
            dp[i] = minn + 1;
        }
        return dp[n];
    }
}
  1. 零钱兑换
class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int coin : coins) {
                if (i < coin) {
                    continue;
                }
                dp[i] = Math.min(dp[i], dp[i - coin]);
            }
            dp[i] += 1;
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
}

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int coin : coins) {
                if (i < coin) {
                    continue;
                }
                dp[i] = Math.min(dp[i], dp[i - coin] + 1);
            }
        }
        return (dp[amount] == amount + 1) ? -1 : dp[amount];
    }
}
  1. 分割等和子集
class Solution {
    public boolean canPartition(int[] nums) {
        if (nums == null || nums.length == 0) {
            return false;
        }
        int len = nums.length;
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (sum % 2 != 0)
            return false;
        int target = sum / 2;
        int[] dp = new int[target + 1];
        for (int i = 0; i < len; i++) {
            for (int j = target; j >= nums[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }

            if (dp[target] == target) {
                return true;
            }
        }
        return dp[target] == target;
    }
}

多维动态规划

技巧

  1. 只出现一次的数字
class Solution {
    public int singleNumber(int[] nums) {
        int ans = 0;
        for (int num : nums) {
            ans ^= num;
        }
        return ans;
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1383678.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2-6基础算法-快速幂/倍增/构造

2-6基础算法-快速幂/倍增/构造

文章目录 一.快速幂二.倍增三.构造 一.快速幂 快速幂算法是一种高效计算幂ab的方法&#xff0c;特别是当b非常大时。它基于幂运算的性质&#xff0c;将幂运算分解成一系列的平方操作&#xff0c;以此减少乘法的次数。算法的核心在于将指数b表示为二进制形式&#xff0c;并利用…
阅读更多...
计算机毕业设计----Springboot+Vue调查问卷管理系统

计算机毕业设计----Springboot+Vue调查问卷管理系统

基于Spring Boot的问卷调查系统 项目介绍 > * 本项目的在线问卷调查调查系统是基于SpringBoot开发的&#xff0c;采用了前后端分离模式来开发。 > * 前端开发使用了Vue、Element UI&#xff0c;后端的开发则是使用了SpringBoot、MyBatis技术。 项目配置 > * 下载…
阅读更多...
docker部署开原博客系统halo

docker部署开原博客系统halo

1.先看下效果 2.拉取镜像 docker pull halohub/halo:2.10 3.启动 mkdir -p /data/halo && cd /data/halodocker run -it -d --name halo -p 8090:8090 -v /data/halo/.halo2:/root/.halo2 halohub/halo:2.10 4.设置账户密码 设置后登陆 5.登陆 发布博客
阅读更多...
【Docker】Dockerfile构建最小镜像

【Docker】Dockerfile构建最小镜像

&#x1f973;&#x1f973;Welcome 的Huihuis Code World ! !&#x1f973;&#x1f973; 接下来看看由辉辉所写的关于Docker的相关操作吧 目录 &#x1f973;&#x1f973;Welcome 的Huihuis Code World ! !&#x1f973;&#x1f973; 前言 一.Dockerfile是什么 二.Dock…
阅读更多...
【Qt】QThread moveTothread-多线程的两种实现方法

【Qt】QThread moveTothread-多线程的两种实现方法

一、如何理解多线程 二、实现多线程的两种方式&#xff08;面向应用&#xff09; 2.1 继承 QThread 的类 2.2 (推荐这种方式)函数 moveTothread() 三、多线程的释放问题&#xff08;善后工作&#xff09; 多线程的两种实现方法 一、如何理解多线程二、实现多线程的两种方式&…
阅读更多...
C++核心编程之类和对象---C++面向对象的三大特性--多态

C++核心编程之类和对象---C++面向对象的三大特性--多态

目录 一、多态 1. 多态的概念 2.多态的分类&#xff1a; 1. 静态多态&#xff1a; 2. 动态多态&#xff1a; 3.静态多态和动态多态的区别&#xff1a; 4.动态多态需要满足的条件&#xff1a; 4.1重写的概念&#xff1a; 4.2动态多态的调用&#xff1a; 二、多态 三、多…
阅读更多...
快速排序学习笔记

快速排序学习笔记

代码框架 // 在数组nums将下标从left到right中进行从小到大排序// 原理是先将一个元素排好序&#xff0c;然后将其他的元素排好序void sort(int[] nums, int left, int right) {if (left > right) {return;}// 对数组nums[left,right]进行切分&#xff0c;使得nums[left,p-1…
阅读更多...
Pandoc：markdown转word

Pandoc：markdown转word

简介&#xff1a;Pandoc是由John MacFarlane开发的标记语言转换工具&#xff0c;可实现不同标记语言间的格式转换&#xff0c;堪称该领域中的“瑞士军刀”。Pandoc使用Haskell语言编写&#xff0c;以命令行形式实现与用户的交互&#xff0c;可支持多种操作系统&#xff1b;Pand…
阅读更多...
A connection was successfully established with the server but then an error

A connection was successfully established with the server but then an error

在使用EFCore生成数据库的时候&#xff0c;报上面的错误&#xff01; 解决方法&#xff1a; 加&#xff08;EncryptTrue;TrustServerCertificateTrue;&#xff09;即可&#xff1a; "ConnectionStrings": { "DefaultConnection": "Data SourceLAP…
阅读更多...
大厂咋做支付系统的核对？

大厂咋做支付系统的核对？

核对是保障资金安全的重要机制。 时效角度&#xff0c;主要有&#xff1a; &#xff08;准&#xff09;实时核对 准确性不如离线核对&#xff0c;且需相应实时核对平台建设 离线核对&#xff08;如 T1 核对&#xff09; 主要问题是发现问题的时机较为后置&#xff0c;部分场景…
阅读更多...
软件测试|教你使用Python下载图片

软件测试|教你使用Python下载图片

前言 我一直觉得Windows系统默认的桌面背景不好看&#xff0c;但是自己又没有好的资源可以进行替换&#xff0c;突然我一个朋友提醒了我&#xff0c;网络上的图片这么多&#xff0c;你甚至可以每天换很多个好看的背景&#xff0c;但是如果让我手动去设置的话&#xff0c;我觉得…
阅读更多...
Consider defining a bean of type ‘XXXX‘ in your configuration.

Consider defining a bean of type ‘XXXX‘ in your configuration.

今天学习尚硅谷的SpringCloud时&#xff0c;发现支付模块无法启动&#xff0c;控制台输出下面的错误: 看起来可能是dao层没有被注入。 然后根据我已有的知识&#xff0c;我检查了注解Mapper Mapper public interface PaymentDao {public int create(Payment payment);public…
阅读更多...
Nacos下载与安装【Linux】

Nacos下载与安装【Linux】

&#x1f95a;今日鸡汤&#x1f95a; 我不是天生的王者&#xff0c;但我骨子里流动着不让我低头的血液。 ——《海贼王》 目录 &#x1f32d;1.官网下载 &#x1f37f;2.根据需求下载Linux版本 &#x1f953;3.上传到Linux &#x1f9c2;4.解压Nacos &#x1f9c8; 5.…
阅读更多...
C++力扣题目701--二叉搜索树中的插入操作

C++力扣题目701--二叉搜索树中的插入操作

给定二叉搜索树&#xff08;BST&#xff09;的根节点 root 和要插入树中的值 value &#xff0c;将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 &#xff0c;新值和原始二叉搜索树中的任意节点值都不同。 注意&#xff0c;可能存在多种有效的插入方式&a…
阅读更多...
温和去油去黑头，只需敷上一刻钟的泥膜就够了

温和去油去黑头，只需敷上一刻钟的泥膜就够了

冬季天气干燥&#xff0c;很多朋友脸部更容易出油&#xff0c;连带着黑头也变多了。这是因为干燥的环境会刺激皮脂腺分泌&#xff0c;导致皮肤油脂分泌过多&#xff0c;容易堵塞毛孔形成黑头。因此&#xff0c;在冬季特别需要注意控油去黑头的工作。 控油去黑头需要清洁毛孔&am…
阅读更多...
Sentinel微服务保护

Sentinel微服务保护

文章目录 Sentinel微服务保护1.初识Sentinel1.1.雪崩问题及解决方案1.1.1.雪崩问题1.1.2.解决方案1.1.3.总结 1.2.服务保护技术对比1.3.Sentinel介绍和安装1.3.1.初识Sentinel1.3.2.安装Sentinel 1.4.微服务整合Sentinel 2.流量控制2.1.簇点链路2.1.快速入门2.2.流控模式2.2.1.…
阅读更多...
docker应用：vocechat

docker应用：vocechat

简介&#xff1a;VoceChat是一款超轻量级的Rust聊天应用程序、API和SDK&#xff0c;优先考虑私人托管。使用VoceChat建立您自己的聊天功能&#xff01;作为一款非常好用的通讯应用程序&#xff0c;它可以让你与朋友、家人和同事进行即时消息聊天&#xff0c;支持图片视频的分享…
阅读更多...
Python相对导入和绝对导入

Python相对导入和绝对导入

目录结构&#xff1a; 在 en_de_model_CDDD.py 文件有两种导入方式可以导入utils.py&#xff0c;分别是 相对导入&#xff1a; from ...public_utils.utils import canonicalize_smiles 绝对导入&#xff1a; from public_utils.utils import canonicalize_smiles 这里推荐使…
阅读更多...
Fluent 动网格应用：2.5D 网格重构

Fluent 动网格应用：2.5D 网格重构

1 概述 2.5D 网格重构是一种快速网格重构方法&#xff0c;主要应用于涡旋压缩机等存在复杂平面运动且无法简化为二维计算的问题。 涡旋压缩机工作原理&#xff08;视频源&#xff1a;维基百科&#xff09; 适用于 2.5D 动网格的问题特点&#xff1a; 计算域几何形状为柱体类形…
阅读更多...
WorkPlus企业内部即时通信新选择，打造高效协作新格局

WorkPlus企业内部即时通信新选择，打造高效协作新格局

在企业内部&#xff0c;快速、高效的沟通与协作是推动工作进程的关键。而即时通信工具成为了企业内部沟通的重要工具。作为一款优秀的企业内部即时通信工具&#xff0c;WorkPlus通过其出色的性能和独特的功能&#xff0c;为企业打造高效协作的新格局。 为什么选择WorkPlus作为企…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023