C++力扣题目701--二叉搜索树中的插入操作

news2025/1/24 11:40:36

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回 任意有效的结果 。

示例 1：

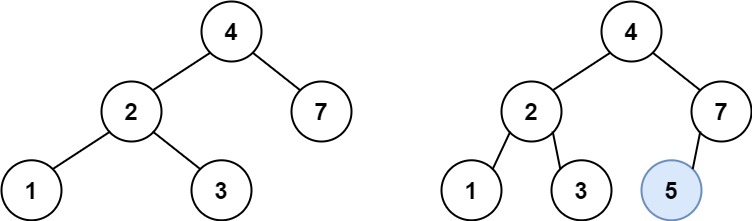
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

树中的节点数将在 [0, 104]的范围内。
-108 <= Node.val <= 108
所有值 Node.val 是 独一无二 的。
-108 <= val <= 108
保证 val 在原始BST中不存在。

思路

这道题目其实是一道简单题目，但是题目中的提示：有多种有效的插入方式，还可以重构二叉搜索树，一下子吓退了不少人，瞬间感觉题目复杂了很多。

其实可以不考虑题目中提示所说的改变树的结构的插入方式。

如下演示视频中可以看出：只要按照二叉搜索树的规则去遍历，遇到空节点就插入节点就可以了。

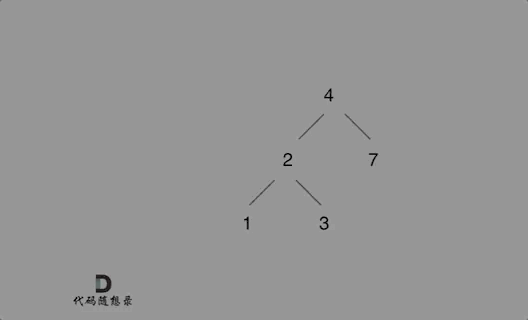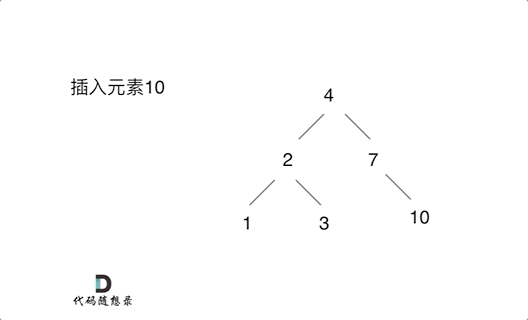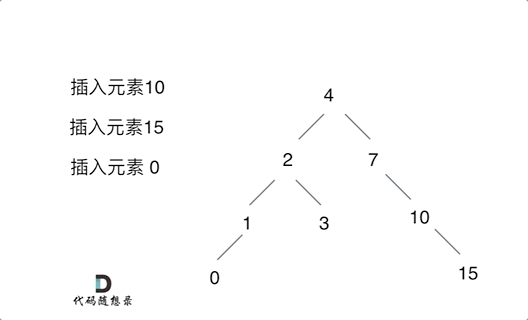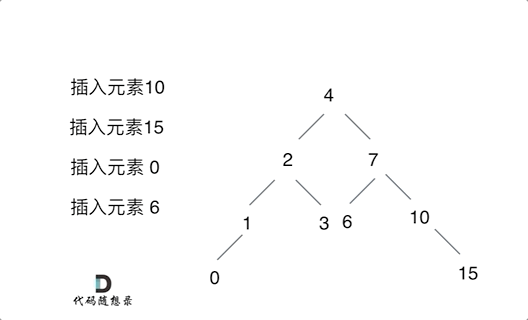
701.二叉搜索树中的插入操作

例如插入元素10 ，需要找到末尾节点插入便可，一样的道理来插入元素15，插入元素0，插入元素6，需要调整二叉树的结构么？并不需要。。

只要遍历二叉搜索树，找到空节点插入元素就可以了，那么这道题其实就简单了。

接下来就是遍历二叉搜索树的过程了。

#递归

递归三部曲：

确定递归函数参数以及返回值

参数就是根节点指针，以及要插入元素，这里递归函数要不要有返回值呢？

可以有，也可以没有，但递归函数如果没有返回值的话，实现是比较麻烦的，下面也会给出其具体实现代码。

有返回值的话，可以利用返回值完成新加入的节点与其父节点的赋值操作。（下面会进一步解释）

递归函数的返回类型为节点类型TreeNode * 。

代码如下：

TreeNode* insertIntoBST(TreeNode* root, int val)

确定终止条件

终止条件就是找到遍历的节点为null的时候，就是要插入节点的位置了，并把插入的节点返回。

代码如下：

if (root == NULL) {
    TreeNode* node = new TreeNode(val);
    return node;
}

这里把添加的节点返回给上一层，就完成了父子节点的赋值操作了，详细再往下看。

确定单层递归的逻辑

此时要明确，需要遍历整棵树么？

别忘了这是搜索树，遍历整棵搜索树简直是对搜索树的侮辱。

搜索树是有方向了，可以根据插入元素的数值，决定递归方向。

代码如下：

if (root->val > val) root->left = insertIntoBST(root->left, val);
if (root->val < val) root->right = insertIntoBST(root->right, val);
return root;

到这里，大家应该能感受到，如何通过递归函数返回值完成了新加入节点的父子关系赋值操作了，下一层将加入节点返回，本层用root->left或者root->right将其接住。

整体代码如下：

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        if (root->val > val) root->left = insertIntoBST(root->left, val);
        if (root->val < val) root->right = insertIntoBST(root->right, val);
        return root;
    }
};

可以看出代码并不复杂。

刚刚说了递归函数不用返回值也可以，找到插入的节点位置，直接让其父节点指向插入节点，结束递归，也是可以的。

那么递归函数定义如下：

TreeNode* parent; // 记录遍历节点的父节点
void traversal(TreeNode* cur, int val)

没有返回值，需要记录上一个节点（parent），遇到空节点了，就让parent左孩子或者右孩子指向新插入的节点。然后结束递归。

代码如下：

class Solution {
private:
    TreeNode* parent;
    void traversal(TreeNode* cur, int val) {
        if (cur == NULL) {
            TreeNode* node = new TreeNode(val);
            if (val > parent->val) parent->right = node;
            else parent->left = node;
            return;
        }
        parent = cur;
        if (cur->val > val) traversal(cur->left, val);
        if (cur->val < val) traversal(cur->right, val);
        return;
    }

public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        parent = new TreeNode(0);
        if (root == NULL) {
            root = new TreeNode(val);
        }
        traversal(root, val);
        return root;
    }
};

可以看出还是麻烦一些的。

我之所以举这个例子，是想说明通过递归函数的返回值完成父子节点的赋值是可以带来便利的。

网上千篇一律的代码，可能会误导大家认为通过递归函数返回节点这样的写法是天经地义，其实这里是有优化的！

#迭代

再来看看迭代法，对二叉搜索树迭代写法不熟悉，可以看这篇：二叉树：二叉搜索树登场！(opens new window)

在迭代法遍历的过程中，需要记录一下当前遍历的节点的父节点，这样才能做插入节点的操作。

在二叉树：搜索树的最小绝对差 (opens new window)和二叉树：我的众数是多少？ (opens new window)中，都是用了记录pre和cur两个指针的技巧，本题也是一样的。

代码如下：

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        TreeNode* cur = root;
        TreeNode* parent = root; // 这个很重要，需要记录上一个节点，否则无法赋值新节点
        while (cur != NULL) {
            parent = cur;
            if (cur->val > val) cur = cur->left;
            else cur = cur->right;
        }
        TreeNode* node = new TreeNode(val);
        if (val < parent->val) parent->left = node;// 此时是用parent节点的进行赋值
        else parent->right = node;
        return root;
    }
};