原题链接:https://www.luogu.com.cn/problem/P1439
题目描述
给出 1,2,…,n 的两个排列 P1 和 P2 ,求它们的最长公共子序列。
输入格式
第一行是一个数 n。
接下来两行,每行为 n 个数,为自然数 1,2,…,n 的一个排列。
输出格式
一个数,即最长公共子序列的长度。
输入输出样例
输入 #1
5 3 2 1 4 5 1 2 3 4 5
输出 #1
3
说明/提示
- 对于 50% 的数据, n≤1e3;
- 对于 100% 的数据, n≤1e5。
解题思路:
首先一看题目,我去这不是经典dp模型最长公共子序列吗,这也太简单了,本来准备直接上最长公共子序列的模板秒了,但是一看数据范围,n=1e5,最长公共子序列模板题的时间复杂度为O(n^2),这里的n=1e5,时间复杂度就到达了1e10,这也太高了,这个时间复杂度肯定过不了,这个时候肯定是观察状态转移方程根据状态转移方程看能不能进行优化,一看状态转移方程好像找不到什么好的优化方式,这个优化方式不存在,我们再看是否能够挖掘什么性质进行优化,我们可以发现a,b数组都是一个1-n的一个排列,也就是说俩个数组中都是1-n中的每个数只出现一次,下面让我们来画一个图模拟一下题目给出的样例,看看是否具有什么性质。
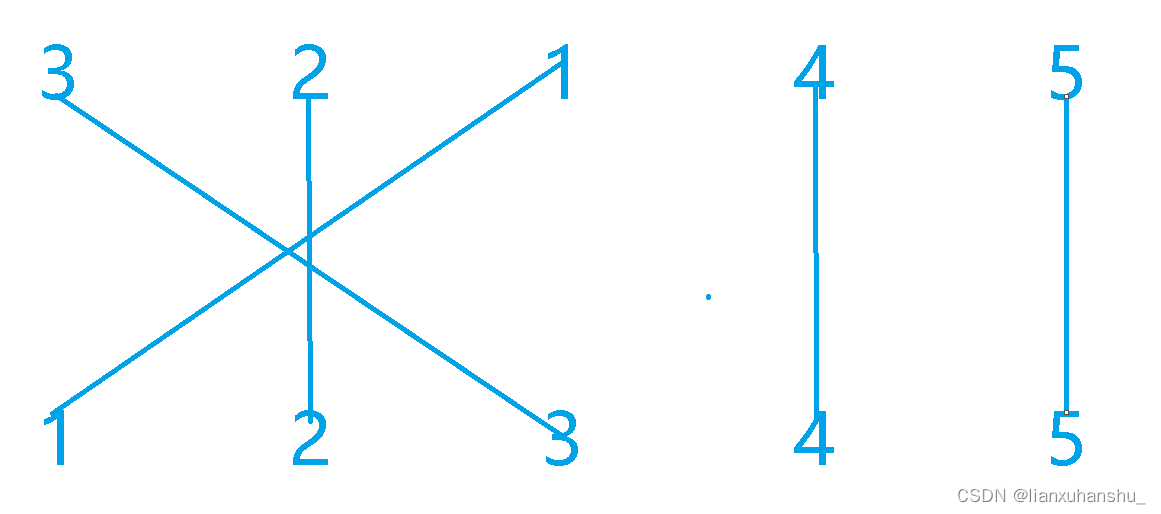
(1):首先我们知道公共子序列是每个位置都对应相等的,例如上述图中描述的样例,如果我们选择3,那么第一个序列的3和第二个序列的3就都要选上,那么此时就无法选择1和2,因为如果还选择1,那么第一个序列中选出的就是[3,1],第二个序列中选出的就是[1,3],这样俩个序列都不相同的了,肯定是不行的,然后如果选择2第一个序列就是[3,2],第二个序列就是[2,3]了,这也肯定是不行的,但是我们选择1之后是可以选择4和5的,这个时候我们就可以发现一个明显的性质了,这个性质就是我们将俩个数组a和b数值相等的位置连线之后,我们选择的公共子序列的所有数值对的连线不能不能存在交叉的现象。
(2):那么我们怎么保证我们选择的所有数值对的连线不交叉呢,我们可以根据数组a各个元素的相对位置来进行对应映射对数组b进行重新赋值,例如上述图中样例,在数组a中3位于第一个位置,所以将b数组中的3重新赋值为1 ,数组a中2位置第二个位置,所以将b数组中的2重新赋值为2,其他的也是如下赋值即可,这样原来的数组b为[1,2,3,4,5],就转换为了[3,2,1,4,5],对于映射之后重新赋值的新数组b,选择了某个位置之后,就不能选择b之前比当前选择位置大的数,不能选择b之后比当前位置小的数,例如这个新b数组选择了1之后,就不能选择1之前的2,3,但是可以选择1之后的4,5,看到这个这不就是求最长上升子序列吗,这个时候我们就将题目原本的求最长公共子序列变为了求新的b数组最长上升子序列,这个题目n=1e5,不能采用最长上升子序列的朴素dp写法,因为最长上升子序列的朴素dp写法时间复杂度为O(n^2),这个复杂度过不了,应该采用最长上升子序列的二分+贪心的那个写法,这种写法时间复杂度为O(nlogn),这个时间复杂度是可以过的。
时间复杂度:将原本求最长公共子序列转换为求映射的新数组b的最长上升子序列,使用求最长上升子序列的二分+贪心写法时间复杂度为O(nlogn)
总结:这个题目属于诈骗题了,题目表面是求最长公共子序列,但是n非常大,n=1e5,显然最长公共子序列的那个O(n^2)解法过不了,观察状态转移方程也没有发现很明显的优化方式,但是我们画图之后发现了一个性质,就将原本的求最长公共子序列变为了求最长上升子序列,然后采用最长上升子序列二分+贪心写法这个题目就可以过了,这个题目纯属套着羊皮的狼,挂羊头卖狗肉,题目给的虽然是求最长公共子序列,但是本质上就是求最长上升子序列。
启发:
至于我为什么能发现这个性质是因为我做一个非常像的题,所以很快就发现了这个性质,很快就解决了这个题目,所以说还是需要学会知识的迁移吧,对于学到的东西多加总结融会贯通还是有好处的,这样对于学过的东西,以后遇到类似的题目还是有帮助的。
那个很像的题目的链接:https://www.acwing.com/problem/content/1014/
cpp代码如下
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N], b[N], f[N];
int q[N];
int main()
{
cin >> n;
unordered_map<int, int> mp;
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]), mp[a[i]] = i;
for (int i = 1; i <= n; i++)
scanf("%d", &b[i]), b[i] = mp[b[i]]; // 根据a数组对b数组重新赋值,映射出一个新的b数组
// 对于新映射出的b数组求最长上升子序列,这里是最长上升子序列的二分+贪心的写法,时间复杂度O(nlogn)
int len = 0;
for (int i = 1; i <= n; i++)
{
int l = 0, r = len;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (q[mid] < b[i])
l = mid;
else
r = mid - 1;
}
len = max(len, r + 1);
q[r + 1] = b[i];
}
// len记录的就是新b数组的最长上升子序列
cout << len << endl;
return 0;
}