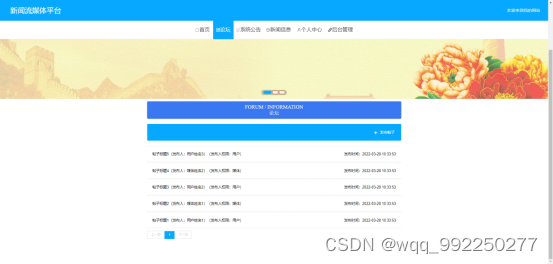
对一元二次方程ax²+bx+c=0 (a≠0);若判别式△=b²-4ac<0,则方程无实根,虚数解为:x=(-b± i√(4ac-b²))/(2a)。
只含有一个未知数(一元),并且未知数项的最高次数是2(二次)的整式方程叫做一元二次方程[1] 。一元二次方程经过整理都可化成一般形式ax²+bx+c=0(a≠0)。其中ax²叫作二次项,a是二次项系数;bx叫作一次项,b是一次项系数;c叫作常数项。一元二次方程成立必须同时满足三个条件:①是整式方程,即等号两边都是整式,方程中如果有分母;且未知数在分母上,那么这个方程就是分式方程,不是一元二次方程,方程中如果有根号,且未知数在根号内,那么这个方程也不是一元二次方程(是无理方程)。②只含有一个未知数;③未知数项的最高次数是2。

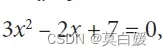
解:
Δ=(-2)^2-4×3×7=-80
√Δ=√-80=√80×√-1=(2√10)i
(i=√-1,称为虚数单位)
X=(-(-2)±√Δ)/2
=〔4±(2√10)i〕/2
=2±(√10)i
即:X1=2+(√10)i
X2=2-(√10)i
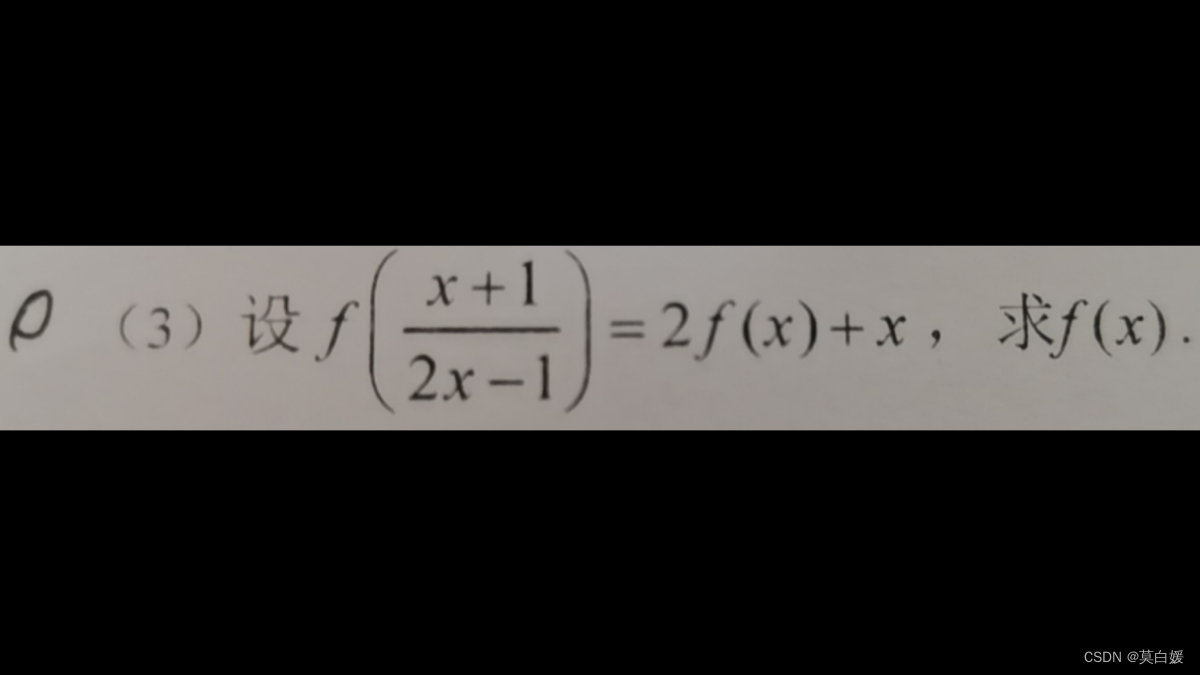
一元二次方程虚数解
news2026/2/13 3:19:01
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1383197.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
SpringCloud:微服务
文章目录 微服务服务架构演变单例架构(集中式架构)分布式架构 微服务SpringCloud 微服务
服务架构演变
单例架构(集中式架构)
单例架构: 将业务的所有功能集中在一个项目中开发,打成一个包部署 优点&…
CSS基础笔记-05layout
CSS基础笔记系列
《CSS基础笔记-01CSS概述》《CSS基础笔记-02动画》《CSS基础笔记-03选择器》《CSS基础笔记-04cascade-specificity-inheritance》 文章目录 CSS基础笔记系列什么是CSS布局布局方法normal flowflexboxgridfloats 总结 什么是CSS布局
CSS布局是指在页面中对元素…
Compileflow工作流引擎使用讲解
文章目录 1 Compileflow1.1 简介1.2 特点1.3 Compileflow插件下载1.4 main方法调用1.4.1 pom.xml1.4.2 新建bpm文件1.4.3 各个节点绑定方法1.4.4 测试方法 1.5 bpm各个标签说明1.5.1 BPM根节点1.5.2 全局变量1.5.3 开始节点: start1.5.4 结束节点: end1.5.5 自动节点: autoTask…
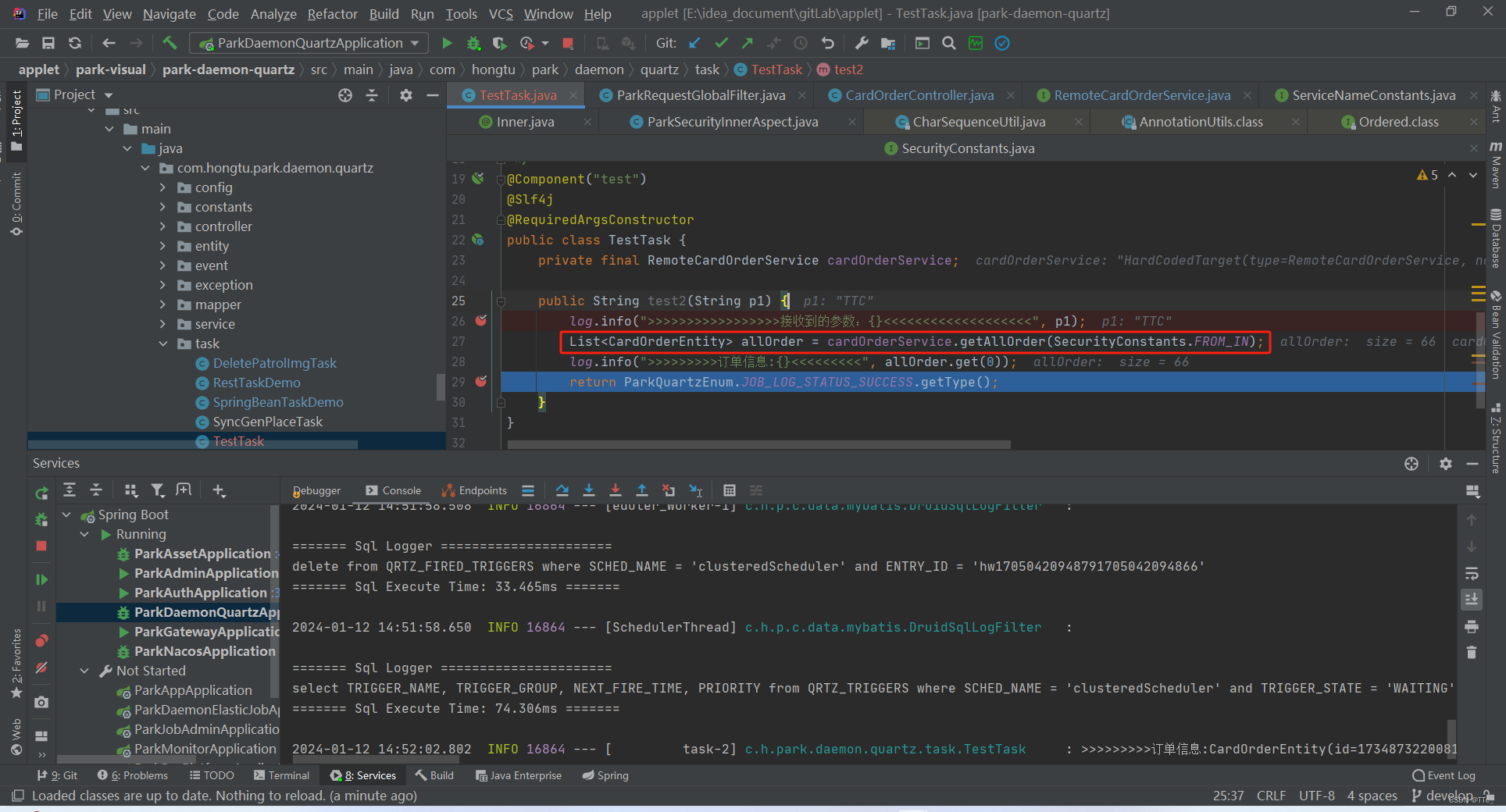
关于Quartz远程调用服务方法失败如何解决,@Inner详细介绍
1.单独在要调用服务的controller写上相关方法(Inner(value true)要走aop,会检测是否有内部调用标识)具体见下述 2. 编写Feign远程调用的接口,注意加上RequestHeader(SecurityConstants.FROM) String from。因为inner(value true…
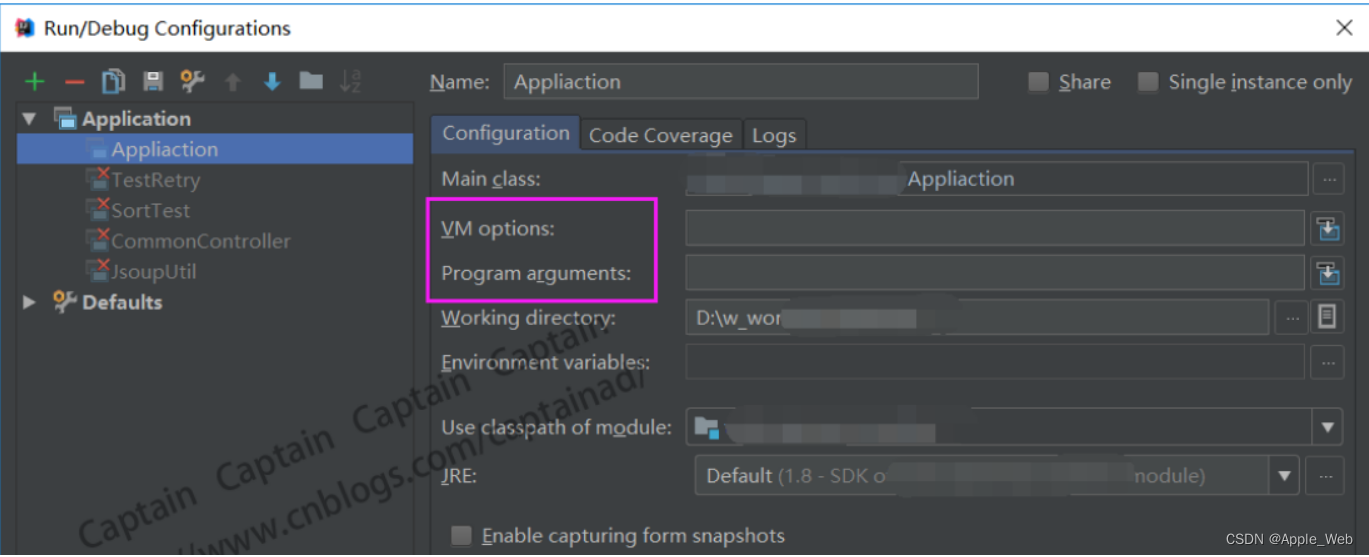
带你拿捏SpringBoot自动装配的核心技术?模块装配(@EnableXXX注解+@Import)+ 条件装配(@ConditionalXXX)
文章目录 Profile激活指定配置文件主配置文件中指定激活的profile命令行激活设置虚拟机参数激活 profile控制不到的地方 Spring原生的条件装配注解ConditionalConditional接口讲解案例讲解 Spring Boot封装的条件装配注解ConditionalXXX自己实现ConditionalOnBeanSpringBoot 源…
【目标检测】评价指标:mAP概念及其计算方法(yolo源码/pycocotools)
本篇文章首先介绍目标检测任务中的关键评价指标mAP的概念;然后介绍其在yolo源码和pycocotools工具中的实现方法;最后比较两种mAP的计算方法的不同之处。 目标检测中的评价指标:
mAP概念及其计算方法(yolo源码/pycocotools) 混淆矩阵概念及其…
6.2 声音编辑工具GoldWave5简介(7)
6.2.5其它常用功能
1.高低通
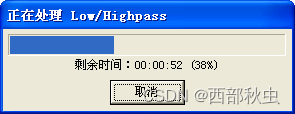
把录制的语音和背景音乐融合在一起时,可能会出现背景音乐音量过大,语音音量过小的现象,这时可以选择“低通”将背景音乐的音量降低一些。
(1)选择【效果】|【波波器】|【低通/高通】命令࿰…
开箱即用的企业级前后端分离【.NET Core6.0 Api + Vue 2.x + RBAC】权限框架-Blog.Core
前言
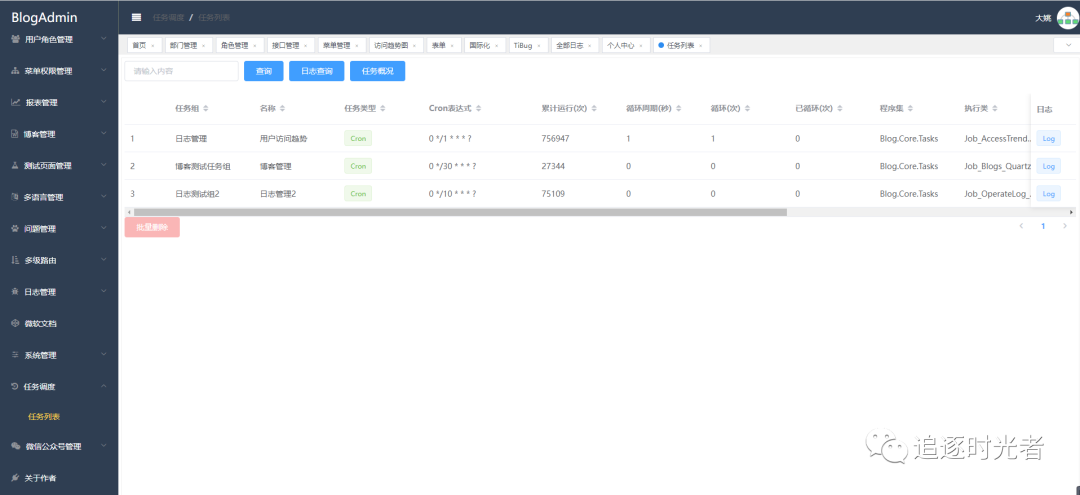
今天要给大家推荐一个开箱即用的企业级前后端分离【.NET Core6.0 Api Vue 2.x RBAC】权限框架(提高生产效率,快速开发就选它):Blog.Core。
推荐原因 Blog.Core通过详细的文章和视频讲解,将知识点各个击破&…
2024-1-12 关于SVPWM的理解疑问
直流母线电压利用率是指逆变电路(电机控制器)所能输出的交流电压基波最大幅值U1m和直流母线电压之比。
电压利用率 SVPWM算法理解(二)——关于非零基本矢量幅值和线电压幅值的解释
因此我们在实际应用中提供的直流侧电压Udc&…
ssm基于Web的课堂管理系统设计与实现论文
目 录
目 录 I 摘 要 III ABSTRACT IV 1 绪论 1 1.1 课题背景 1 1.2 研究现状 1 1.3 研究内容 2 2 系统开发环境 3 2.1 vue技术 3 2.2 JAVA技术 3 2.3 MYSQL数据库 3 2.4 B/S结构 4 2.5 SSM框架技术 4 3 系统分析 5 3.1 可行性分析 5 3.1.1 技术可行性 5 3.1.2 操作可行性 5 3…
【Linux】 系统目录结构
进入到根目录 cd /ls目录名具体作用/存放系统系统相关的目录文件/boot放置linux系统内核文件和启动时用到的一些引导文件/home包含linux系统上各用户的主目录,子目录名称默认以该用户名命名/root系统管理员root的家目录/bin包含常用的命令文件(如ls 等&a…
STM32 CAN学习(一)
STM32 CAN
CAN协议简介
CAN是控制器局域网络(Controller Area Network)的简称,它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的,并最终成为国际标准(ISO11519),是国际上应用最广泛的现场总线之一。CAN总线协…
Qat++,轻量级开源C++ Web框架
目录
一.简介
二.编译Oat
1.环境
2.编译/安装
三.试用
1.创建一个 CMake 项目
2.自定义客户端请求响应
3.将请求Router到服务器
4.用浏览器验证 一.简介
Oat是一个面向C的现代Web框架 官网地址:https://oatpp.io github地址:https://github.co…
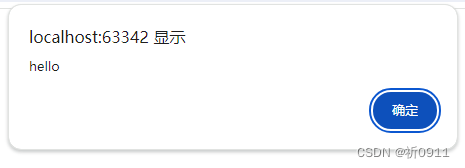
JavaScript中alter、confrim、prompt的区别及使用
文章目录 一、alter1.什么是alert?2.alter的使用 二、confrim1.什么是confrim?2.confrim的使用 三、prompt1.什么是prompt?2.prompt的使用 四、总结alter、confrim、prompt的区别 一、alter
1.什么是alert?
在JavaScript中&…
ssm基于Vue的健身房会员管理系统+vue论文
摘 要
互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面。它让信息都可以通过网络传播,搭配信息管理工具可以很好地为人们提供服务。针对信息管理混乱,出错率高,信息安全性差&#x…
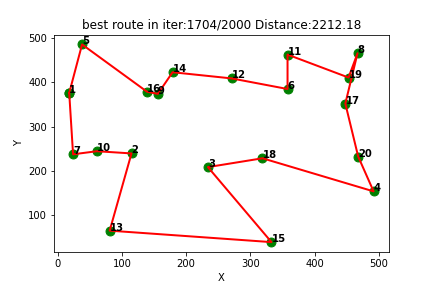
强化学习应用(四):基于Q-learning算法的无人车配送路径规划(提供Python代码)
一、Q-learning算法介绍
Q-learning是一种强化学习算法,用于解决基于环境的决策问题。它通过学习一个Q-table来指导智能体在不同状态下采取最优动作。下面是Q-learning算法的基本步骤:
1. 定义环境:确定问题的状态和动作空间,并…
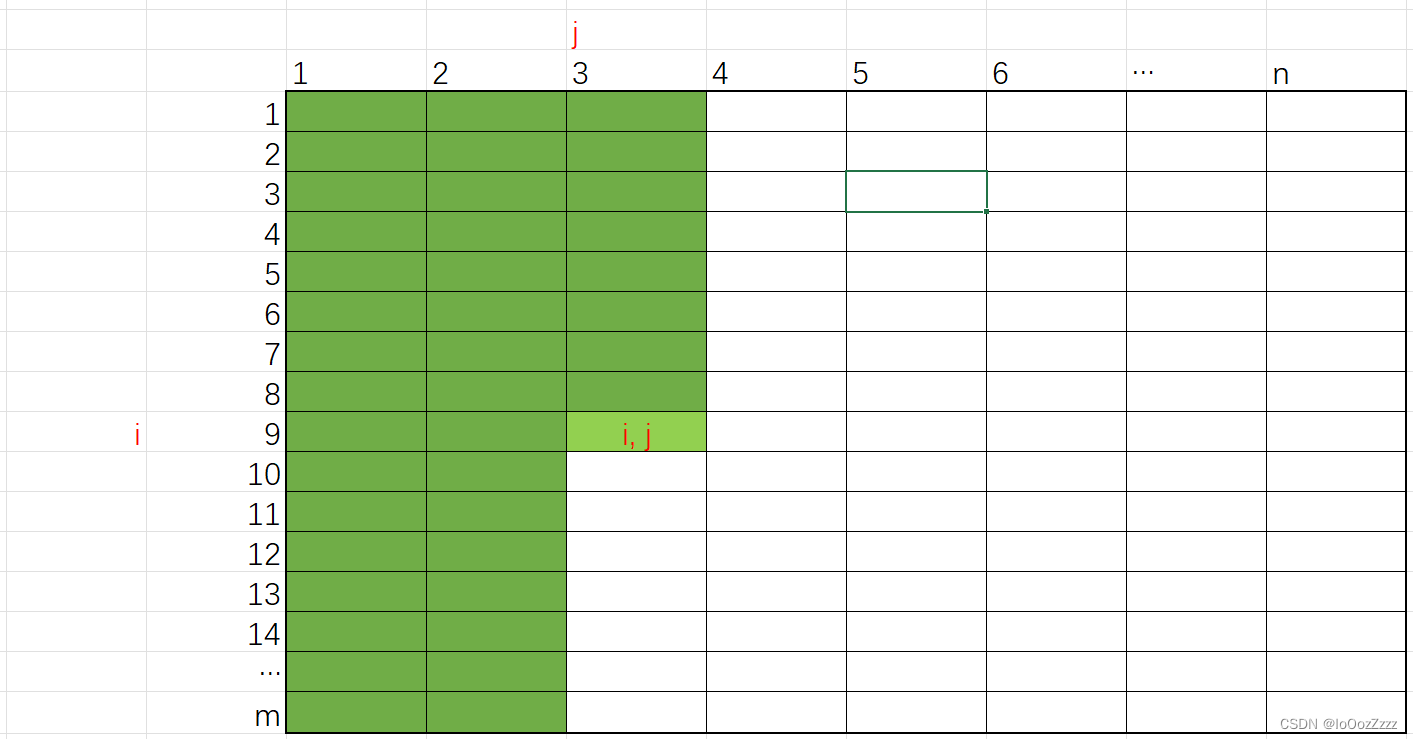
1.5矩阵元素的引用
通过下标来引用矩阵的元素
A(3, 2)表示A矩阵第3行第2列的元素。
>> arr [1,2,3;4,5,6];
>> arr(4, 5) 10arr 1 2 3 0 04 5 6 0 00 0 0 0 00 0 0 0 10>> 如果引用元素超过矩阵的大小将自…
ssm基于spring和vue开发的web新闻流媒体平台论文
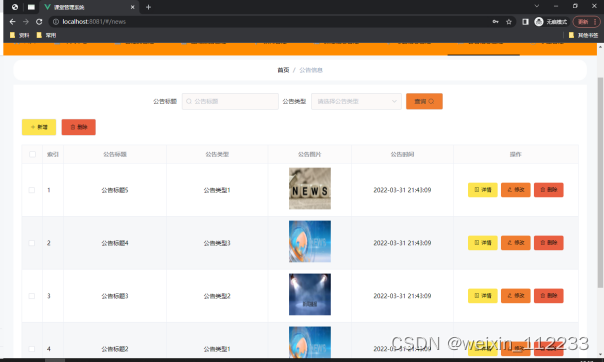
摘 要
如今的时代,是有史以来最好的时代,随着计算机的发展到现在的移动终端的发展,国内目前信息技术已经在世界上遥遥领先,让人们感觉到处于信息大爆炸的社会。信息时代的信息处理肯定不能用之前的手工处理这样的解决方法&#x…
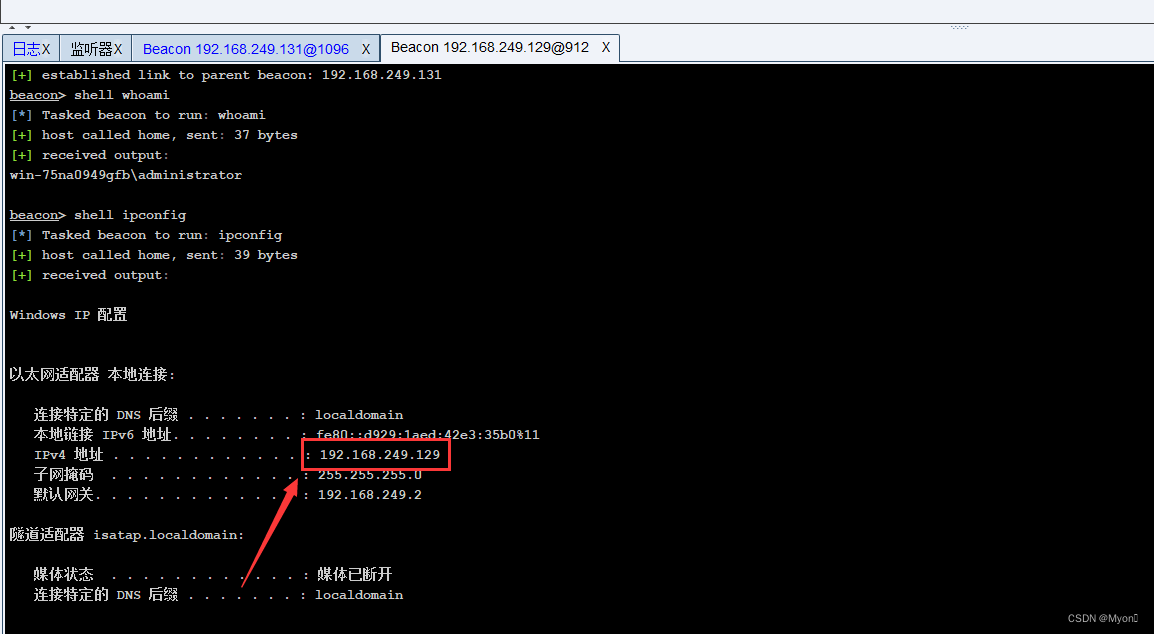
隧道应用3-Cobalt Strike正反向连接多层内网
Cobalt Strike 正向连接多层内网:
teamserver 不允许访问 B ,但是服务器上A有权限( A 与 B 在同一网段),若 A 服务上已经有了 cs 的后门,则可以通过 cs 的正向连接去连接 B ,在 teamserver 通…