高斯Hack算法

news2025/2/27 10:30:28

背景

刷leetcode时，碰到一题需要求解n个bit中选择m个bit的所有组合集，我只想到了递归求解，没啥问题，但是在官方题解中看到了牛逼的方法(Gosper's Hack)，故记录一下。

4bit中2个1的情况

0011b
0101b
0110b
1001b
1010b
1100b

解法

递归求解

/**
 *
 * @param retain 剩余可选1的个数
 * @param start 下一个可选坐标，范围[0,max)
 * @param max 最大边界值
 * @param val 路径val
 * @param result 结果集
 */
private void getSelectOptions(int retain, int start, int max, int val, List<Integer> result){
    if (retain == 0){
        result.add(val);
        return;
    }
    if (start >= max){
        return;
    }
    // 这个位置不填1
    this.getSelectOptions(retain,  start+1, max, val, result);
    // 这个位置填1
    this.getSelectOptions(retain-1,  start+1, max, val | (1 << (max - 1 - start)),result);
}

// 获取结果
List<Integer> selectOptions = new LinkedList<>();
this.getSelectOptions(numSelect, 0, 12, 0, selectOptions);

这个有个缺点，就是遍历了所有的case。个人感觉不是很优雅

Gosper’s Hack

思路

人工写出4个bit中2个1的所有场景，可以这么写0011b,0101b,0110b,1001b,1010b,1100b
它的处理步骤如下：

找到最右边的1，假设位置为i
从[i,31]中找到最右端的1，假设替换位置为j(j>i)
将[0,j)中所有的1全部移到最右边
循环处理

干，语文不好，描述的不太清楚，可以看看参考文章

代码

/**
* 获取所有bit组合数
* @param limit 总共bit数
* @param select 选取的bit数
* @return
*/
public static List<Integer> getAllBitCombination(int limit, int select){
	// 边界值处理
   if (limit >= 31 || limit <= 0 || select <= 0 || limit < select){
       return new LinkedList<>();
   }
   List<Integer> result = new LinkedList<>();
   int val = (1 << select) - 1, r, t;  //1
   int max = 1 << limit; //2
   while (val < max){ //3
       // 将符合条件的数加入结果集
       result.add(val);//4
       // 获取val中最右边的1
       r = val & -val;//5
       // 最右边的1进位左移，替换左边的第一个0槽位
       t = val + r;//6
       val = (((val ^ t) / r)  >> 2)| t;//7
   }
   return result;
}

解读

测试case

4bit中里面存在2个1的解集
即limit=4，select=2

步骤1

获取最小符合条件的解

1 << 2 => 0100b => 4
(1<<2)-1 => 0011b => 3

步骤2

获取最大边界值
1<<4 => 10000 => 16

步骤3

循环获取值，知道超过边界值

步骤4

加有效的结果集加入，或者可以直接进行结果处理

步骤5

获取val中最右边的1，例如011010对应的结果为000010

步骤6

最右边的一向左扫描，替换首个碰到的零。例如011010变成011100

步骤7

(val^t)

获取步骤6中变更的路径

val                                           0 1 1 0 1 1 0 b
r                                             0 0 0 0 0 1 0 b
t                                             0 1 1 1 0 0 0 b
val^t                                         0 0 0 1 1 1 0 b

(val^t)/r

处理相对偏移量。移除右边的零，因为要将所有的1放到右边

val                                           0 1 1 0 1 1 0 b
r                                             0 0 0 0 0 1 0 b
t                                             0 1 1 1 0 0 0 b
val^t                                         0 0 0 1 1 1 0 b
(val^t)/r                                     0 0 0 0 1 1 1 b

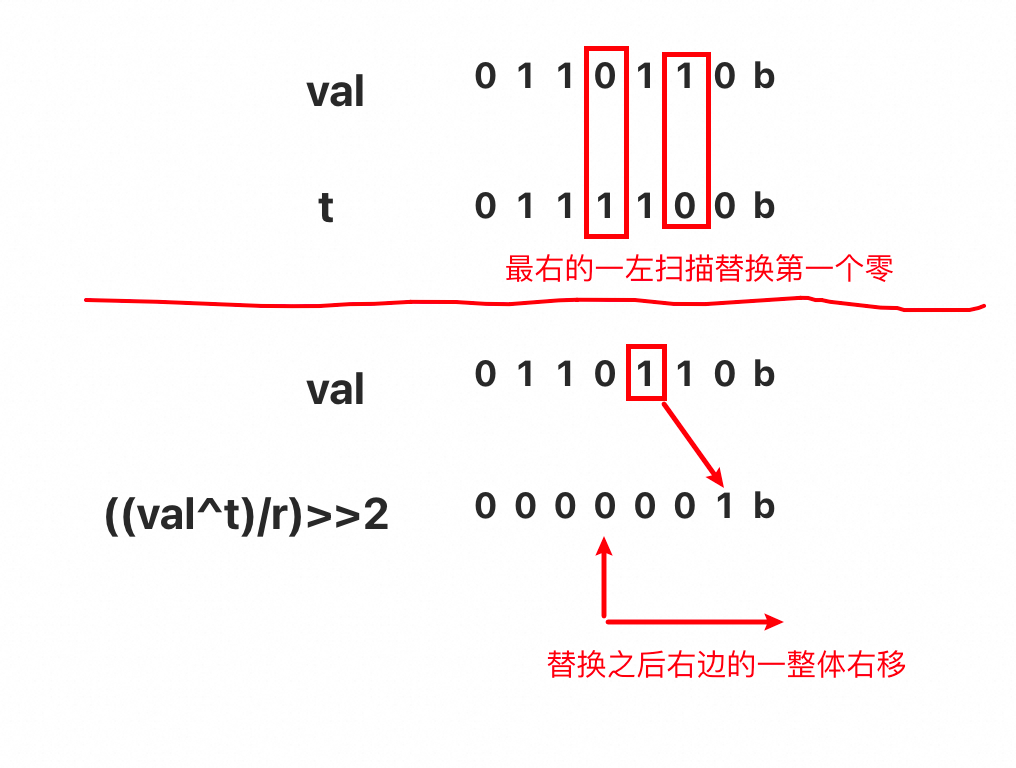
((val^t)/r)>>2

移除两个变更点，原来是1的变成0，原来是0的变成1

val                                           0 1 1 0 1 1 0 b
r                                             0 0 0 0 0 1 0 b
t                                             0 1 1 1 0 0 0 b
val^t                                         0 0 0 1 1 1 0 b
(val^t)/r                                     0 0 0 0 1 1 1 b
((val^t)/r)>>2                                0 0 0 0 0 0 1 b