系列文章目录
前言
关节空间运动模型描述了在闭环关节空间位置控制下机械手的运动,在关节空间运动模型(jointSpaceMotionModel)对象和关节空间运动模型块中使用。
机器人机械手是典型的位置控制设备。要进行关节空间控制,需要指定关节角度或位置向量 q,以跟踪参考配置 q 参考 . 为此,您可以对机器人关节进行闭环控制,并使用运动模型模拟机器人在此控制下的行为。

要使这种方法最接近实际系统的运动,就必须准确表示控制器和被控对象的动态。本主题将介绍在闭环联合空间位置控制下的机器人行为建模方法:
- 作为受计算扭矩控制的系统
- 作为受 PD 控制的系统
- 作为具有独立关节运动的系统
一、背景介绍
1.1 关节空间运动模型与任务空间运动模型
一般来说,机器人位置控制分为两类:
- 关节空间运动控制 - 在这种情况下,机器人的位置输入被指定为一个关节角度或位置向量,即机器人的关节配置 q。 ref 这也被称为配置空间控制。
- 任务空间运动控制 - 将位置指定为控制器的末端执行器姿势。然后,控制器驱动机器人的关节配置值将末端执行器移动到指定位置。这有时被称为操作空间控制。
下图显示了这两种运动控制中不同类型的输入/输出。
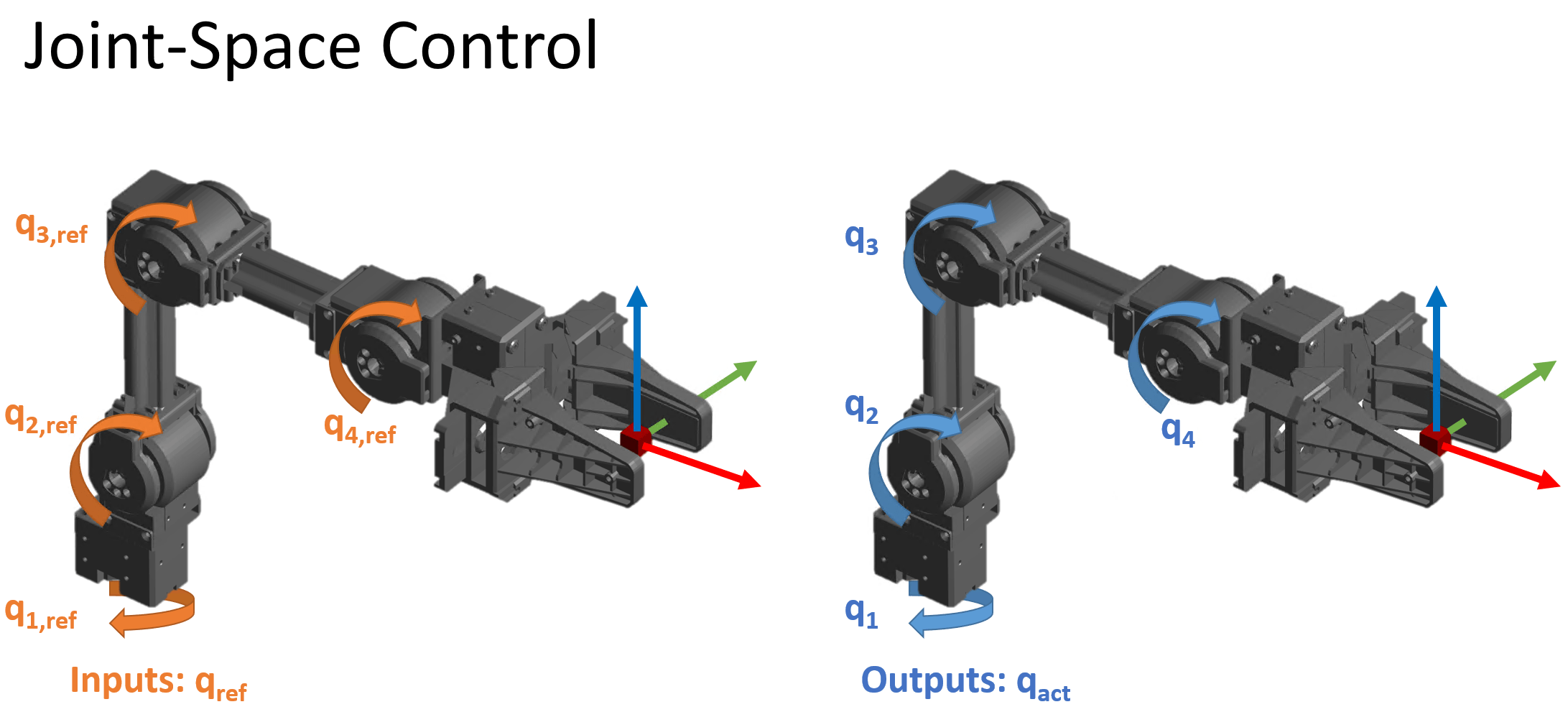

本专题页专门讨论关节空间运动控制,如 jointSpaceMotionModel 对象和关节空间运动模型块中所使用。有关任务空间运动模型,请参阅任务空间运动模型对象。如需更详细了解任务空间和联合空间控制之间的区别,请参阅使用 KINOVA Gen3 机械手计划和执行任务空间和联合空间轨迹的示例。
1.2 在 MATLAB® 和 Simulink® 中使用
关节空间运动模型可以在 MATLAB 或 Simulink 中表示。
在 Simulink 中,关节空间运动模型块接受参考输入和可选外力(如适用),并返回关节配置、速度和加速度。该程序块可处理积分,因此无需额外的积分。
在 MATLAB 中,jointSpaceJointModel 系统对象对闭环运动进行建模。导数方法返回关节配置、速度和加速度在每一时刻的导数,因此必须使用 ODE 求解器或等效的外部积分方法来模拟时间运动。
有关更具体的概述,请参阅相关文档页面。
二、状态
关节空间运动模型的状态由这些值组成:
q - 机器人关节配置,作为关节位置矢量。旋转关节以 rad 为单位,棱柱关节以 m 为单位。
- 关节速度矢量,旋转关节以
为单位,棱柱关节以
为单位。
- 关节加速度矢量,对于旋转关节,单位为
;对于棱柱关节,单位为
三、闭环关节空间运动类型的运动方程
当需要闭环控制下系统的低保真模型,且输入指定为关节配置、速度和加速度时,可使用关节空间运动模型。运动模型包括三种整体行为建模方式:
- 计算转矩控制下的系统 - 刚体动力学建模采用标准刚体机器人动力学,但对全身动力学进行补偿并分配误差动力学。
- PD 控制下的系统 - 刚体动力学建模采用标准刚体机器人动力学,并通过比例-派生 (PD) 控制和重力补偿提供关节扭矩输入。该模型所代表的控制器没有对刚体运动的整体效应进行严格补偿。
- 作为具有独立关节运动的系统 - 每个关节都被独立建模为配置不变的闭环二阶系统。该模型的保真度较低,忽略了机器人的动态特性,并假定为闭环响应。在没有外力作用的情况下,该模型可视为闭环运动的最佳表现形式,因为其动力学特性已被简化并直接规定。
要设置这些不同的运动类型,请使用 jointSpaceMotionModel 对象的 MotionType 属性。这些运动类型并不是详尽无遗的,但它们确实提供了一组在近似系统闭环行为时可以使用的选项。有关何时使用哪种模型的详细信息和建议,请参阅以下章节。
在接下来的章节中,将按照复杂程度递减的顺序介绍每种模型的运动方程。这里的复杂度是指特定运动模型的计算量。高复杂度变量通过直接模拟环路内的控制器和动力学来模拟受相当先进的控制器影响的动力学,而低复杂度模型则使用简化的动力学来表示整体误差行为。
3.1 符号和术语
闭环系统的许多运动方程都源自标准刚体机器人动力学,后者定义了机器人的开环运动。此外,方程中还经常会使用一个斜杠来表示误差动态,例如 。
3.2 计算扭矩控制
当运动模型被定义为受计算扭矩控制的机器人时,运动模型使用标准刚体机器人动力学,但广义力输入由控制法则提供,该法则对刚体动力学进行补偿,并分配二阶误差动力学响应。
输入 - 该模型接受 作为所需的参考关节配置、速度和加速度矢量。用户还可以选择提供一个外力和扭矩矩阵 Fext,以牛顿和牛顿-米为单位,使用 externalForce 函数生成。
输出 - 模型以向量形式输出关节配置、速度和加速度 。在 MATLAB 版本的模型中,只返回加速度,用户必须选择积分器或 ODE 解算器来返回其他状态。
复杂性--这是一个高复杂性模型。运动模型使用带有可选外力的全刚体动力学,控制器作为闭环系统的一部分进行建模,控制器包含动态补偿项。
何时应用 - 当模拟的闭环系统具有可近似误差的动力学特性时,或当使用的控制器将机器人视为多体系统,且可能存在外力时,可使用该功能。
由此产生的闭环系统旨在实现第 i 个关节的以下第二误差行为:
这些参数描述了为每个关节定义的理想响应:
- 自然频率,单位为赫兹
ζ - 阻尼比,无单位
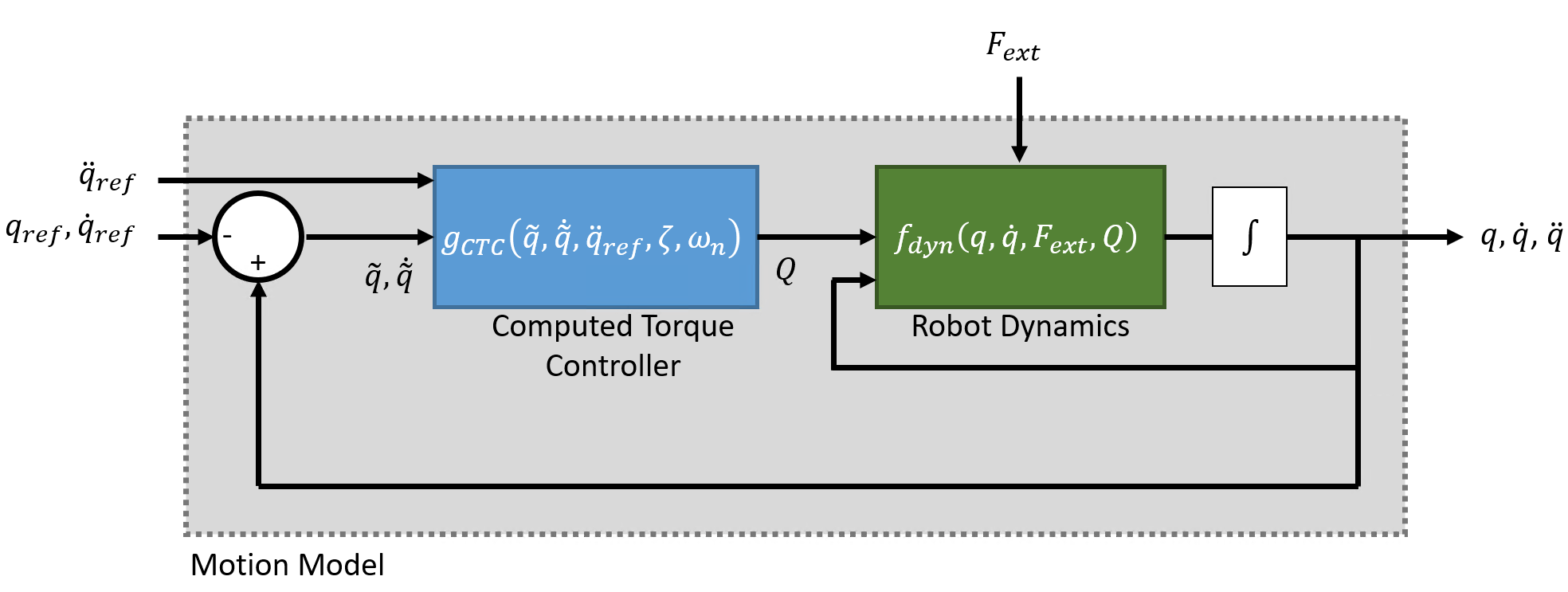
如图所示,整个系统由标准刚体机器人动力学和控制法则组成,控制法则通过广义力输入 Q 强化闭合误差动力学:
其中
M(q) - 是基于当前机器人配置的联合空间质量矩阵 使用 massMatrix 对象函数计算该矩阵。
- 科里奥利项。它与关节速度一起构成速度乘积
,可使用速度乘积对象函数计算。
G(q) - 在指定重力条件下,由于作用在机器人上的重力重量和力量,所有关节为保持其位置所需的力矩和力量。使用重力力矩对象函数计算重力力矩。
- 关节空间运动模型(jointSpaceMotionModel)对象的自然频率(NaturalFrequency)属性中的自然频率 N 乘 N 对角矩阵,单位为 Hz(
)。
- 自然频率 n 的平方乘积与 jointSpaceMotionModel 对象的 DampingRatio 属性中指定的阻尼比 ζ 的 N-by-N 对角矩阵。
ωn 和 ζ 的值可以直接设置,也可以使用 updateErrorDynamicsFromStep 方法提供,该方法根据所需的单位步响应(使用瞬态行为特征定义)计算 ωn 和 ζ 的值。
由于对动态进行了补偿,因此在没有外力输入的情况下,假设反馈项连续积分且无时间延迟,就能实现误差动态。因此,在没有外力的情况下,独立关节运动类型为相同运动提供了一种更简单的建模方式。
有关机器人动力学的更多信息,请参阅机器人动力学。
3.3 比例-微分 (PD) 控制
当机器人被定义为受 PD 控制的系统时,机器人将根据标准刚体机器人动力学建立行为模型,但其广义力输入 Q 由控制法则给出,该法则根据关节误差和重力补偿应用 PD 控制。
输入 - 该模型接受 作为所需的参考关节配置和速度(以向量形式指定)。用户还可以选择提供外力和扭矩 Fext,以牛顿和牛顿-米为单位,使用 externalForce 函数生成。
输出--模型输出 为关节配置、速度和加速度。在 MATLAB 版本的模型中,只返回加速度,用户必须选择积分器或 ODE 求解器来返回其他状态。
复杂性 - 中等复杂性。运动模型使用带有可选外力的全刚体动力学,控制器作为闭环系统的一部分建模,但控制器相对简单。
何时应用 - 当模拟的闭环系统使用将关节视为独立系统的控制器时,或使用 PD 型控制器且可能存在外力时,请使用该控制器。
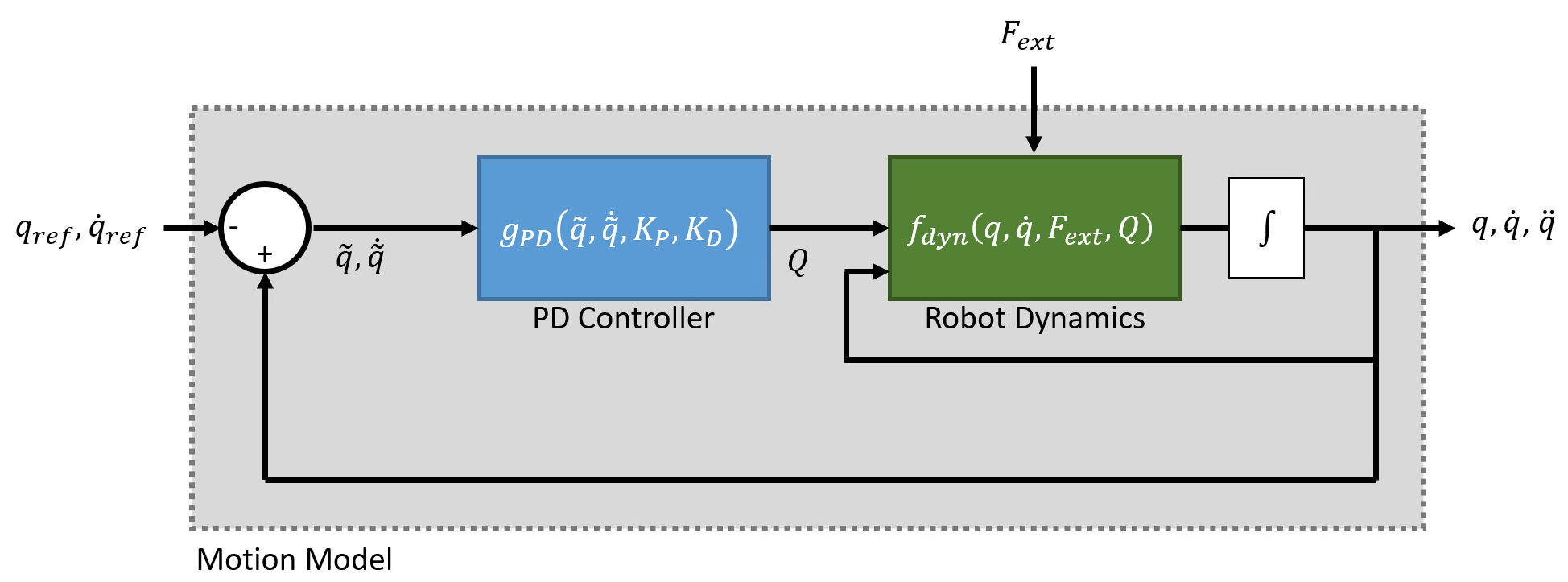
与计算扭矩控制一样,该系统行为采用标准刚体机器人动力学,但使用 PD 控制法定义广义力输入 Q:
其中
G(q) - 是所有关节在刚体树的重力属性中指定的重力下保持位置所需的重力扭矩和力。使用 gravityTorque 对象函数计算重力扭矩。
控制输入依赖于这些用户定义的参数:
- 比例增益,指定为 N 乘 N 矩阵,其中 N 为机械手可移动关节的数量
- 微分增益,指定为 N 乘 N 矩阵
3.4 独立关节运动
在对该系统进行独立关节运动建模时,不是将闭环系统建模为标准刚体机器人动力学加控制输入,而是将每个关节建模为二阶系统,该系统已具有所需的误差行为:
- 输入 - 该模型接受
作为所需的参考关节配置和速度(以矢量形式给出)。没有外力输入。
- 输出 - 模型输出
作为关节配置、速度和加速度。在该模型的 MATLAB 版本中,只返回加速度,用户必须选择积分器或 ODE 求解器来返回其他状态。
- 复杂性 - 复杂性较低。运动模型只是规定了位置控制器可以实现的误差行为。
- 何时应用 - 当系统具有可近似的误差动态,且不需要外力输入时使用。
该系统为第 i 个关节建立了以下闭环二阶行为模型:
- 自然频率,单位为赫兹
ζ - 阻尼比,无单位


因此,整个系统的模型为
该模型依赖于这些用户定义的参数:
- JointSpaceMotionModel 对象的 NaturalFrequency 属性中自然频率的 N-by-N 对角矩阵,单位为 Hz (s-1)。
- 自然频率平方和 ωn 与 jointSpaceMotionModel 对象的 DampingRatio 属性中指定的阻尼比 ζ 的乘积的 N-by-N 对角矩阵。
ωn 和 ζ 的值可以直接设置,也可以使用 updateErrorDynamicsFromStep 方法提供,该方法根据所需的单位步响应(使用瞬态行为特征定义)计算 ωn 和 ζ 的值。
独立关节运动模型代表了理想化行为下的闭环系统。在没有外力的情况下,假设反馈没有延迟(如连续积分),使用计算扭矩控制的运动模型会产生等效输出。





![[Linux 进程(三)] 进程优先级,进程间切换,main函数参数,环境变量](https://img-blog.csdnimg.cn/direct/49deb30dde714671887307d9a11f1390.png)