一.各种函数的用法
1.tf2zp函数:通常用于将传递函数(Transfer Function)转换为零极增益形式(ZPK form),转换前G(s) = num(s) / den(s),转换后G(s) = K * (s - z1) * (s - z2) * ... * (s - zn) / (s - p1) * (s - p2) * ... * (s - pn)
2.zp2tf函数:用于将零极增益形式(ZPK form)转换为传递函数(Transfer Function)形式。转换前G(s) = K * (s - z1) * (s - z2) * ... * (s - zn) / (s - p1) * (s - p2) * ... * (s - pn),转换后G(s) = num(s) / den(s)
3.tf2sos函数:用于将传递函数(Transfer Function)转换为其次数最低的分数形式(SOS form,即Sum-of-Squares form)。转换前,G(s) = num(s) / den(s),转换后G(s) = a0 + a1*s + a2*s^2 + b1*s + b2*s^2 + ...
4.sos2tf函数:用于将SOS形式(Sum-of-Squares form)转换为传递函数(Transfer Function)形式,转换前G(s) = a0 + a1*s + a2*s^2 + b1*s + b2*s^2 + ...转换后G(s) = num(s) / den(s),
5.sos2zp函数:用于将SOS形式(Sum-of-Squares form)转换为零极增益形式(Zero-Pole-Gain form),转换前G(s) = a0 + a1*s + a2*s^2 + b1*s + b2*s^2 + ...,转换后G(s) = K * (s - z1) * (s - z2) * ... * (s - zn) / (s - p1) * (s - p2) * ... * (s - pn)
6.zp2sos函数:一种从零极增益形式(ZPK form)转换为二次分式形式(SOS form)的转换函数。它接受系统函数的零-极点增益模型中零点向量z、极点向量p和增益系数k作为输入,并返回系统函数的二次分式模型的系数矩阵sos和增益系数g。转换前G(s) = K * (s - z1) * (s - z2) * ... * (s - zn) / (s - p1) * (s - p2) * ... * (s - pn),转换后G(s) = a0 + a1*s + a2*s^2 + b1*s + b2*s^2 + ...
7.ss2tf函数:用于将状态空间模型(State-Space model)转换为传递函数(Transfer Function)模型,转换前x' = Ax + Bu y = Cx + Du转换后G(s) = num(s) / den(s)
8.tf2ss函数:用于将传递函数(Transfer Function)模型转换为状态空间模型(State-Space model),转换前G(s) = num(s) / den(s),转换后x' = Ax + Bu y = Cx + Du
二、系统函数如下
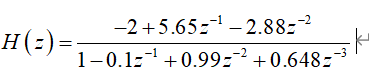
试求出:
极点增益(zpk)模型,用公式编辑器写出其表达式;
极点留数(rpk)模型,用公式编辑器写出其表达式;
二次分式(sos)模型,用公式编辑器写出其表达式。
极点增益(zpk)模型
a=[-2,5.65,-2.88,0];
b=[1,-0.1,0.99,0.648];
[z,p,k]=tf2zp(a,b) %因式分解系统函数

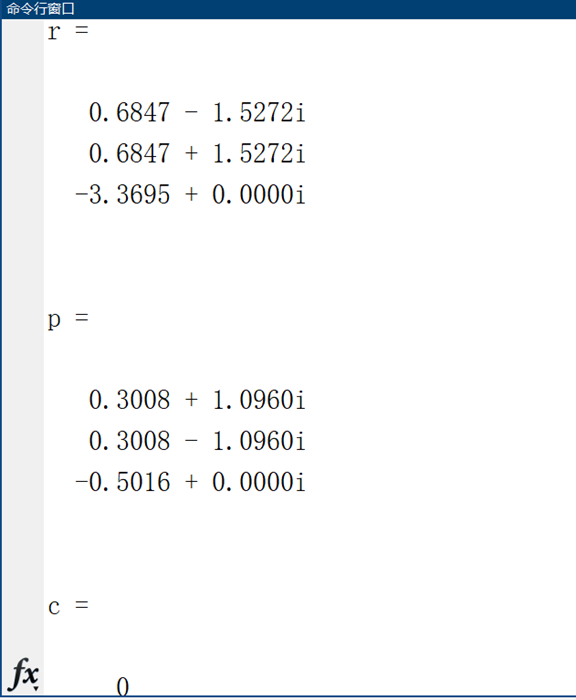
极点留数(rpk)模型
b=[-2,5.65,-2.88,0];
a=[1,-0.1,0.99,0.648];
[r, p, c] = residuez(b, a) %极点求留数
二次分式(sos)模型
num =[-2,5.65,-2.88];
den =[1,-0.1,0.99,0.648];
[A,B]=tf2sos(num,den) %将系统传递函数转换为系统函数二次分式模型

三.LTI的系统函数如下
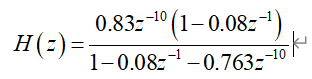
试分析:
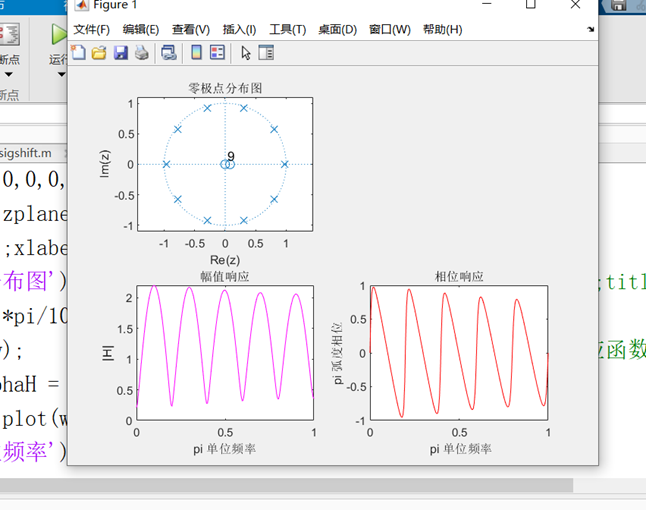
系统的零极点分布,并绘图;
单位冲击响应,并绘图;
分析系统的稳定性;
求出系统的幅频特性和相频特性,并绘图。
a=[0.83,-0.0664];
b=[1,-0.08,0,0,0,0,0,0,0,0,-0.763,0];
subplot(2,2,1);zplane(a,b);
ylabel('Im(z)');xlabel('Re(z)');
title('零极点分布图'); %零极点分布图
subplot(2,2,2);
impz(a,b,200);title('系统单位冲激响应');
w = [0:0.5:100]*pi/100;
H = freqz(b,a,w); %系统的频率响应函数
magH = abs(H);phaH = angle(H); %取角度的绝对值
subplot(2,2,3);plot(w/pi,magH,'m');
xlabel('pi 单位频率');
ylabel('|H|');
title('幅值响应'); %系统的幅频响应
subplot(2,2,4);
plot(w/pi,phaH,'r');
xlabel(' pi 单位频率');
ylabel('pi 弧度相位');
title('相位响应'); %系统的相频响应