今天就带领大家来到树的世界,树无论是在考试上还是实际学习方面都是比较重点的,大家在这块知识要花时间搞懂.
文章目录
前言
一、树的二叉链表定义
二、二叉树三种遍历方式(递归方式)
1.先序遍历方式(根左右)
2.中序遍历方式(左根右)
3.后序遍历方式(左右根)
三、二叉树的层次遍历方式(采用数组模拟队列)
四、已知一颗二叉树的先序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
五、已知一颗二叉树的后序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
六、已知一颗二叉树的层序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
七、二叉树的基本操作
1.求一颗二叉树的节点个数
2.求一棵二叉树的叶子节点个数
3.求一棵二叉树中度为1的节点个数
4.查找二叉树中值为x的节点,若存在则返回存储位置,不存在则返回空值
5.求一棵二叉树的高度
6.求一棵二叉树中值为x的节点作为根节点的子树的深度.
7.交换一棵二叉树的左右子树
8.判断两棵树是否相似(长得一样)
9.判断一棵树是否为完全二叉树
10.设计算法利用叶子节点中的的空指针域将所有的叶子节点,链接成一个带头节点的双链表
11.一个包含二元运算的算数表达式以二叉链表形式存在在二叉树T中,设计算法求解算数表达式
12.求一棵二叉树的最大宽度
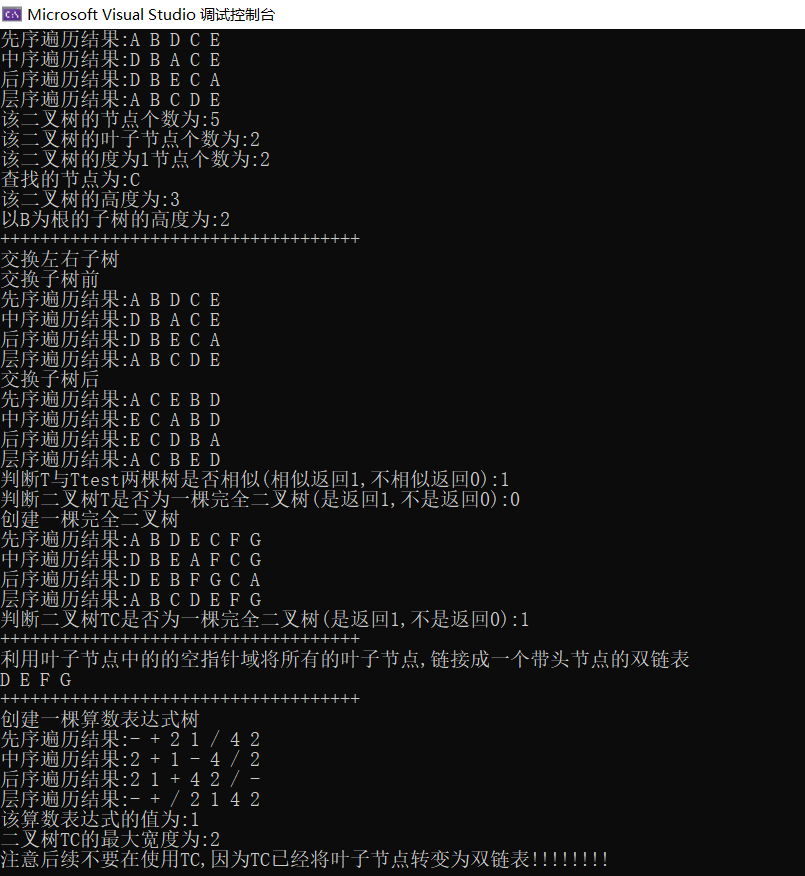
八、总代码与测试结果
前言
树这块的内容比较多,包括树的一些基本的定义以及一些计算,后面还有完全二叉树,排序二叉树,平衡二叉树,这些树可能在定义上不一样但思想都是一样的,平衡二叉树在考试中主要考的是操作,代码实现的话实际上是比较困难的,但在面试时可能会考到,再后面树以及森林等等,后续都会讲到.这节主要是树的基本操作.
一、树的二叉链表定义
typedef char Elemtype;
//树的数据结构二叉链表
typedef struct BiTNode {
Elemtype data;
struct BiTNode* lchild;
struct BiTNode* rchild;
}BiTNode,*BiTree;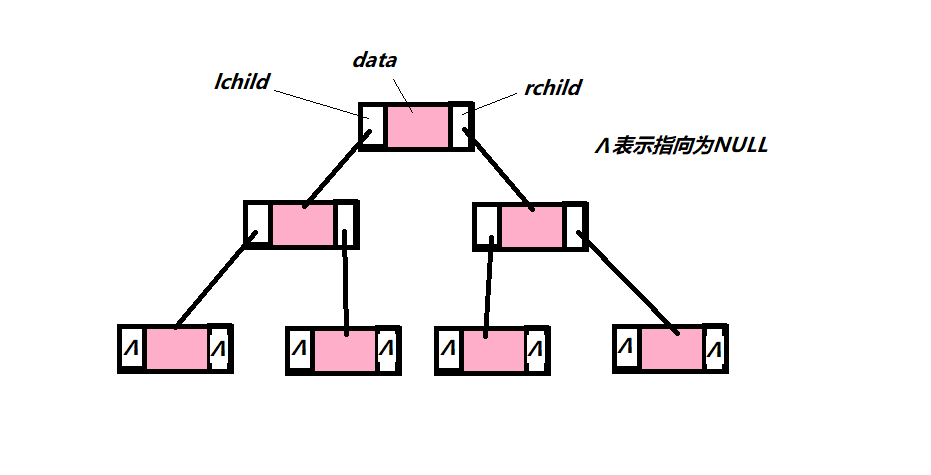
二、二叉树三种遍历方式(递归方式)
1.先序遍历方式(根左右)
//二叉树的先序遍历(根左右)
void preorderTraverse(BiTree T) {
if (T != NULL) {
printf("%c ", T->data);//先访问根节点
preorderTraverse(T->lchild);//遍历左子树
preorderTraverse(T->rchild);//遍历右子树
}
}2.中序遍历方式(左根右)
//二叉树的中序遍历(左根右)
void inorderTraverse(BiTree T) {
if (T != NULL) {
inorderTraverse(T->lchild);
printf("%c ", T->data);
inorderTraverse(T->rchild);
}
}3.后序遍历方式(左右根)
//二叉树的后序遍历(左右根)
void postorderTraverse(BiTree T) {
if (T != NULL) {
postorderTraverse(T->lchild);
postorderTraverse(T->rchild);
printf("%c ", T->data);
}
}三、二叉树的层次遍历方式(采用数组模拟队列)
//二叉树的层次遍历算法
void levelTraverse(BiTree T) {//使用数组模拟队列注意分配长度
BiTNode* Queue[80] = {NULL};//这里就分配了40注意
int front = 0;
int rear = 0;
if (T != NULL) {
Queue[++rear] = T;//根节点入队
}
while (front != rear) {
BiTNode* p = Queue[++front];
printf("%c ", p->data);
if (p!=NULL && p->lchild != NULL) {
Queue[++rear] = p->lchild;
}
if (p != NULL && p->rchild != NULL) {
Queue[++rear] = p->rchild;
}
}
}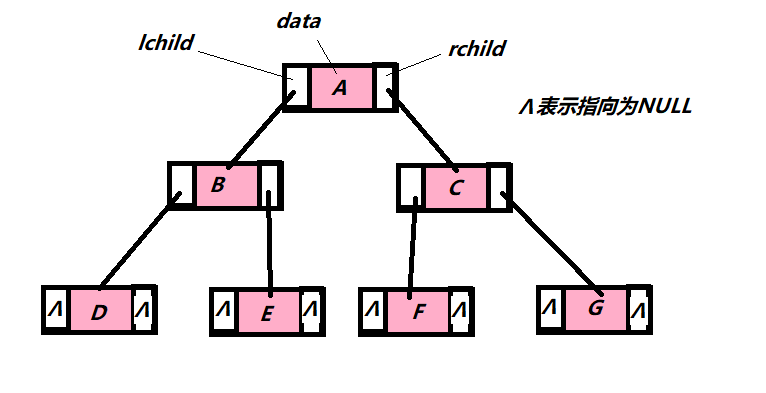
层次遍历序列为:ABCDEFG
算法思想:首先创建一个队列,将根节点先入队列,如果队列不为空循环操作
1.出队
2.有孩子将孩子入队
直到队列为空,遍历完成.
四、已知一颗二叉树的先序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
这题也是建立二叉树的基本算法,自命题考试的时候容易考.
//已知一颗二叉树的先序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
BiTNode* creatBitree1(char pre[], char in[], int l1, int h1, int l2, int h2) {
//l代表第一个元素的位置,h代表最后一个元素的位置
if (l1 > h1) {
return NULL;
}
BiTNode* pNode = (BiTNode*)malloc(sizeof(BiTNode));
assert(pNode);
pNode->data = pre[l1];//在中序遍历中寻找根节点所在位置
int p = l2;
while (p <= h2) {
if (in[p] == pre[l1]) {
break;
}
p++;
}
//p为在数组中下标a减下标b表示a到b中有几个元素算a不算b
pNode->lchild = creatBitree1(pre, in, l1 + 1, l1 + p - l2, l2, p - 1);
pNode->rchild = creatBitree1(pre, in, l1 + p - l2 + 1, h1, p + 1, h2);
return pNode;
}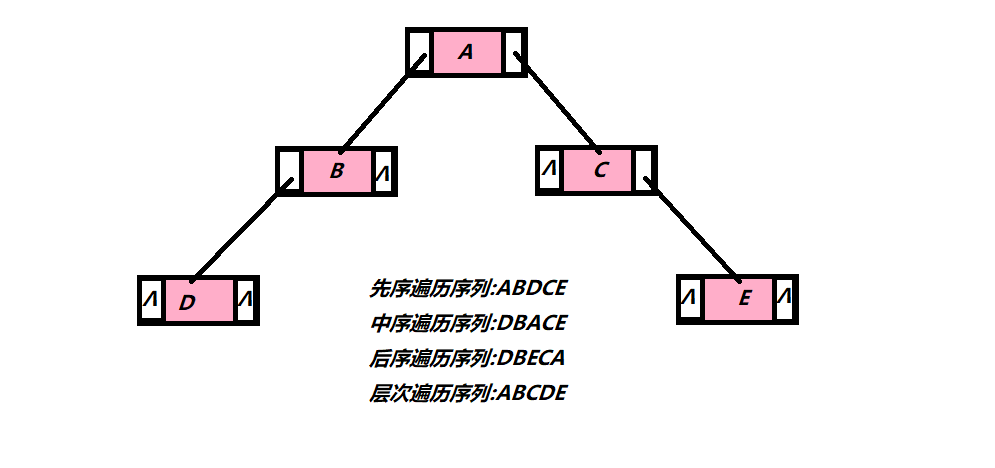
算法思想:使用先序和中序序列构建二叉树,首先我们知道先序序列的第一个节点是跟节点,获得根节点后在中序遍历序列中找到根节点所在位置,那么就能确定左孩子和右孩子序列这样我们在根据先序遍历序列就又能递归的将树建立起来.
五、已知一颗二叉树的后序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
//已知一颗二叉树的后序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
BiTNode* creatBitree2(char post[], char in[], int l1, int h1, int l2, int h2) {
if (l1 > h1) {
return NULL;
}
BiTNode* pNode = (BiTNode*)malloc(sizeof(BiTNode));
assert(pNode);
pNode->data = post[h1];
int p = l2;
while (l2 <= h2) {
if (in[p] == post[h1]) {
break;
}
p++;
}
pNode->lchild = creatBitree2(post, in, l1, l1 + p - l2 - 1, l2, p - 1);
pNode->rchild = creatBitree2(post, in, l1 + p - l2, h1 - 1, p + 1, h2);
return pNode;
}还是根据上图数据.

算法思想;使用后续遍历与中序遍历构建二叉树,首先我们知道后续遍历的最后的一个节点为根节点,这样我们在中序遍历中找到根节点所在位置,那么左子树右子树序列就知道了,再根据后续遍历的最后一个节点为根节点,就能够递归的建立二叉树了.
六、已知一颗二叉树的层序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
//已知一颗二叉树的层序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
BiTNode* creatBitree3(char level[], char in[], int l1, int h1, int l2, int h2) {
if (l1 > h1) {
return NULL;
}
BiTNode* pNode = (BiTNode*)malloc(sizeof(BiTNode));
assert(pNode);
pNode->data = level[l1];
int p = l2;
while (p <= h2) {
if (in[p] == level[l1]) {
break;
}
p++;
}
//寻找左子树和右子树在层次遍历中的顺序
char lelflevel[5];
char rightlevel[5];
int lelflength = 0;
int rightlength = 0;
//左子树
for (int i = l1 + 1; i <= h1; i++) {
for (int j = l2; j < p; j++) {
if (level[i] == in[j]) {
lelflevel[lelflength] = level[i];
lelflength++;
}
}
}
//右子树
for (int i = l1 + 1; i <= h1; i++) {
for (int j = p + 1; j <= h2; j++) {
if (level[i] == in[j]) {
rightlevel[rightlength] = level[i];
rightlength++;
}
}
}
pNode->lchild = creatBitree3(lelflevel, in, 0, lelflength - 1, l2, p - 1);
pNode->rchild = creatBitree3(rightlevel, in, 0, rightlength - 1, p + 1, h2);
return pNode;
}
算法思想:使用层次遍历与中序遍历建立二叉树,首先我们知道先序遍历第一个节点为根节点,这样我们在中序遍历序列中找到根节点所在位置我们就能知道左子树和右子树的序列,但返回层次遍历序列在寻找左右子树序列时,与前两道题不同,由于层次遍历序列只能反映大概位置并不能直接反应左子树和右子树序列,所以我们需要寻找序列,在层次遍历中按顺序判断,该元素是否在左子树序列(或右子树序列)在就加入左子树(或右子树)层次遍历数组中这样我们就得到了,左子树和右子树的层次遍历序列,再根据中序遍历,这样就又能递归的建立二叉树了.
注意:这三种构建二叉树的方式不要先看代码,先不要研究这是怎么来的,先自己根据我所给的二叉树手推一遍,我愿成为上面二叉树的例子,是搞懂这几个算法之神.
七、二叉树的基本操作
1.求一颗二叉树的节点个数
//例1:求一颗二叉树的节点个数
int nodesInBitree(BiTree T) {//递归实现,采用先序遍历算法思想
if (T == NULL) {
return 0;
}
return 1 + nodesInBitree(T->lchild) + nodesInBitree(T->rchild);
}2.求一棵二叉树的叶子节点个数
//例2:求一棵二叉树的叶子节点个数
int leafsInBitree(BiTree T) {//先序遍历的思想
if (T == NULL) {
return 0;
}
else if (T->lchild == NULL && T->rchild == NULL) {//叶子姐姐
return 1;
}
return leafsInBitree(T->lchild) + leafsInBitree(T->rchild);
}3.求一棵二叉树中度为1的节点个数
//例3:求一棵二叉树中度为1的节点个数
int getsinglenodes(BiTree T) {//先序遍历的思想
if (T == NULL) {
return 0;
}
else if (T->lchild != NULL && T->rchild == NULL) {//左子树不为空继续搜索
return 1 + getsinglenodes(T->lchild);
}
else if (T->lchild == NULL && T->rchild != NULL) {//右子树不为空继续搜索
return 1 + getsinglenodes(T->rchild);
}
else {
return getsinglenodes(T->lchild) + getsinglenodes(T->rchild);
}
}4.查找二叉树中值为x的节点,若存在则返回存储位置,不存在则返回空值
//例4:查找二叉树中值为x的节点,若存在则返回存储位置,不存在则返回空值
BiTNode* seekElemNode(BiTree T,char x) {
if (T == NULL) {
return NULL;
}
else if (x == T->data) {
return T;
}
else {
BiTNode* tmp = seekElemNode(T->lchild,x);//搜左子树
if (tmp != NULL) {
return tmp;
}
else {//左子树没有
return seekElemNode(T->rchild,x);//搜右子树
}
}
}5.求一棵二叉树的高度
这个算法一定要熟悉,单独考它不多但它经常处理一些复杂算法中起到作用
//例5:求一棵二叉树的高度
int getBitreehigh(BiTree T) {//递归思想
if (T == NULL) {
return 0;
}
else {
int lelfhigh = getBitreehigh(T->lchild);
int righthigh = getBitreehigh(T->rchild);
return lelfhigh > righthigh ? lelfhigh + 1 : righthigh + 1;
}
}6.求一棵二叉树中值为x的节点作为根节点的子树的深度.
算法思想就是例4和例5结合,先找到值为x的节点,在根据此节点求二叉树的高度
7.交换一棵二叉树的左右子树
//例7:交换一棵二叉树的左右子树
void switchLRchild(BiTree T) {
if (T != NULL) {
BiTNode* tmp = T->lchild;
T->lchild = T->rchild;
T->rchild = tmp;
switchLRchild(T->lchild);
switchLRchild(T->rchild);
}
}8.判断两棵树是否相似(长得一样)
//例8:判断两棵树是否相似(长得一样)
bool issimilarBitree(BiTree T1, BiTree T2) {
if (T1 == NULL && T2 == NULL) {
return true;
}
else if (T1 == NULL && T2 != NULL || T1 != NULL && T2 == NULL) {
return false;
}
else {
return issimilarBitree(T1->lchild, T2->lchild) && issimilarBitree(T1->rchild, T2->rchild);
}
}9.判断一棵树是否为完全二叉树
//例9:判断一棵树是否为完全二叉树
//算法思想:层序遍历树(将空孩子也入队)如果出队的节点为空,是完全二叉树那么队列中的结点都为空,如果有不为空的节点那么就不是完全二叉树
bool isCompleteBitree(BiTree T) {
//应用数组模拟队列
BiTNode* Queue[30];//注意这里数组队列的空间
int front = 0;
int rear = 0;
if (T != NULL) {
Queue[++rear] = T;
}
while (front != rear) {//层次遍历
BiTNode* tmp = Queue[++front];
if (tmp == NULL) {//遇到第一个空姐点退出循环
break;
}
Queue[++rear] = tmp->lchild;
Queue[++rear] = tmp->rchild;
}
while (front != rear) {//判断后续节点是否为空
BiTNode *tmp = Queue[++front];
if (tmp != NULL) {//有节点不为空说明不是完全二叉树
return 0;
}
}
return 1;
}算法思想:层序遍历树(将空孩子也入队)如果出队的节点为空,是完全二叉树那么队列中的结点都为空,如果有不为空的节点那么就不是完全二叉树
10.设计算法利用叶子节点中的的空指针域将所有的叶子节点,链接成一个带头节点的双链表
//例10:设计算法利用叶子节点中的的空指针域将所有的叶子节点,链接成一个带头节点的双链表
void Linkleafs(BiTree T, BiTNode*& pTail) {//采用尾插法这样就不用判断插入的节点是否是第一个节点
if (T != NULL) {
if (T->lchild == NULL && T->rchild == NULL) {//叶子节点
T->lchild = pTail;
pTail->rchild = T;
pTail = T;
}
else {
Linkleafs(T->lchild,pTail);//处理左子树
Linkleafs(T->rchild, pTail);//处理右子树
}
}
}
BiTNode* operatFunc(BiTree T) {
BiTNode* L = NULL;
L = (BiTNode*)malloc(sizeof(BiTNode));
assert(L);
L->lchild = NULL;
L->rchild = NULL;
BiTNode* pTail = L;
Linkleafs(T, pTail);
return L;
}
//打印双链表函数(数据类型char)
void print(BiTNode *L) {
BiTNode* p = L->rchild;
while (p) {
printf("%c ", p->data);
p = p->rchild;
}
printf("\n");
}11.一个包含二元运算的算数表达式以二叉链表形式存在在二叉树T中,设计算法求解算数表达式
//例11:一个包含二元运算的算数表达式以二叉链表形式存在在二叉树T中,设计算法求解算数表达式
int compute(char oprt, int leftnum, int rightnum) {//计算函数
switch (oprt) {
case'+':return leftnum + rightnum; break;
case'-':return leftnum - rightnum; break;
case'*':return leftnum * rightnum; break;
case'/':return leftnum / rightnum; break;
}
}
int getnum(BiTree T) {
if (T == NULL) {//树为空
return 0;
}
else if (T->lchild != NULL && T->rchild != NULL) {//操作符节点
char oprt = T->data;
int leftnum = getnum(T->lchild);
int rightnum = getnum(T->rchild);
return compute(oprt, leftnum, rightnum);//递归求值
}
else {//操作树节点
return T->data - '0';
}
}
//创建一棵算数表达式树
BiTNode* creatoprtBitree() {
char pre[7] = { '-','+','2','1','/','4','2' };
char in[7] = { '2','+','1','-','4','/','2' };
return creatBitree1(pre, in, 0, 6, 0, 6);
}12.求一棵二叉树的最大宽度
//例12:求一棵二叉树的最大宽度
//这里直接用了一个数组直接存储每层的宽度
void getWidthBitree(BiTree T, int level,int wid[],int &max) {
if (T == NULL) return;
wid[level]++;
if (wid[level] > max) max = wid[level];
getWidthBitree(T->lchild, level + 1,wid,max);
getWidthBitree(T->rchild, level + 1,wid,max);
}八、总代码与测试结果
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<malloc.h>
#include<assert.h>
#define MAX 20
typedef char Elemtype;
//树的数据结构二叉链表
typedef struct BiTNode {
Elemtype data;
struct BiTNode* lchild;
struct BiTNode* rchild;
}BiTNode,*BiTree;
//二叉树的先序遍历(根左右)
void preorderTraverse(BiTree T) {
if (T != NULL) {
printf("%c ", T->data);
preorderTraverse(T->lchild);
preorderTraverse(T->rchild);
}
}
//二叉树的中序遍历(左根右)
void inorderTraverse(BiTree T) {
if (T != NULL) {
inorderTraverse(T->lchild);
printf("%c ", T->data);
inorderTraverse(T->rchild);
}
}
//二叉树的后序遍历(左右根)
void postorderTraverse(BiTree T) {
if (T != NULL) {
postorderTraverse(T->lchild);
postorderTraverse(T->rchild);
printf("%c ", T->data);
}
}
//二叉树的层次遍历算法
void levelTraverse(BiTree T) {//使用数组模拟队列
BiTNode* Queue[80] = {NULL};//这里就分配了40注意
int front = 0;
int rear = 0;
if (T != NULL) {
Queue[++rear] = T;//根节点入队
}
while (front != rear) {
BiTNode* p = Queue[++front];
printf("%c ", p->data);
if (p!=NULL && p->lchild != NULL) {
Queue[++rear] = p->lchild;
}
if (p != NULL && p->rchild != NULL) {
Queue[++rear] = p->rchild;
}
}
}
//已知一颗二叉树的先序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
BiTNode* creatBitree1(char pre[], char in[], int l1, int h1, int l2, int h2) {
//l代表第一个元素的位置,h代表最后一个元素的位置
if (l1 > h1) {
return NULL;
}
BiTNode* pNode = (BiTNode*)malloc(sizeof(BiTNode));
assert(pNode);
pNode->data = pre[l1];
int p = l2;
while (p <= h2) {
if (in[p] == pre[l1]) {
break;
}
p++;
}
//在数组中下标a减下标b表示a到b中有几个元素算a不算b
pNode->lchild = creatBitree1(pre, in, l1 + 1, l1 + p - l2, l2, p - 1);
pNode->rchild = creatBitree1(pre, in, l1 + p - l2 + 1, h1, p + 1, h2);
return pNode;
}
//已知一颗二叉树的后序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
BiTNode* creatBitree2(char post[], char in[], int l1, int h1, int l2, int h2) {
if (l1 > h1) {
return NULL;
}
BiTNode* pNode = (BiTNode*)malloc(sizeof(BiTNode));
assert(pNode);
pNode->data = post[h1];
int p = l2;
while (l2 <= h2) {
if (in[p] == post[h1]) {
break;
}
p++;
}
pNode->lchild = creatBitree2(post, in, l1, l1 + p - l2 - 1, l2, p - 1);
pNode->rchild = creatBitree2(post, in, l1 + p - l2, h1 - 1, p + 1, h2);
return pNode;
}
//已知一颗二叉树的层序遍历序列和中序遍历分别存在两个一维数组中试编写算法建立该二叉树的二叉链表
BiTNode* creatBitree3(char level[], char in[], int l1, int h1, int l2, int h2) {
if (l1 > h1) {
return NULL;
}
BiTNode* pNode = (BiTNode*)malloc(sizeof(BiTNode));
assert(pNode);
pNode->data = level[l1];
int p = l2;
while (p <= h2) {
if (in[p] == level[l1]) {
break;
}
p++;
}
//寻找左子树和右子树在层次遍历中的顺序
char lelflevel[5];
char rightlevel[5];
int lelflength = 0;
int rightlength = 0;
//左子树
for (int i = l1 + 1; i <= h1; i++) {
for (int j = l2; j < p; j++) {
if (level[i] == in[j]) {
lelflevel[lelflength] = level[i];
lelflength++;
}
}
}
//右子树
for (int i = l1 + 1; i <= h1; i++) {
for (int j = p + 1; j <= h2; j++) {
if (level[i] == in[j]) {
rightlevel[rightlength] = level[i];
rightlength++;
}
}
}
pNode->lchild = creatBitree3(lelflevel, in, 0, lelflength - 1, l2, p - 1);
pNode->rchild = creatBitree3(rightlevel, in, 0, rightlength - 1, p + 1, h2);
return pNode;
}
//二叉树的基本操作
//例1:求一颗二叉树的节点个数
int nodesInBitree(BiTree T) {
if (T == NULL) {
return 0;
}
return 1 + nodesInBitree(T->lchild) + nodesInBitree(T->rchild);
}
//例2:求一棵二叉树的叶子节点个数
int leafsInBitree(BiTree T) {
if (T == NULL) {
return 0;
}
else if (T->lchild == NULL && T->rchild == NULL) {//叶子姐姐
return 1;
}
return leafsInBitree(T->lchild) + leafsInBitree(T->rchild);
}
//例3:求一棵二叉树中度为1的节点个数
int getsinglenodes(BiTree T) {
if (T == NULL) {
return 0;
}
else if (T->lchild != NULL && T->rchild == NULL) {//左子树不为空继续搜索
return 1 + getsinglenodes(T->lchild);
}
else if (T->lchild == NULL && T->rchild != NULL) {//右子树不为空继续搜索
return 1 + getsinglenodes(T->rchild);
}
else {
return getsinglenodes(T->lchild) + getsinglenodes(T->rchild);
}
}
//例4:查找二叉树中值为x的节点,若存在则返回存储位置,不存在则返回空值
BiTNode* seekElemNode(BiTree T,char x) {
if (T == NULL) {
return NULL;
}
else if (x == T->data) {
return T;
}
else {
BiTNode* tmp = seekElemNode(T->lchild,x);//搜左子树
if (tmp != NULL) {
return tmp;
}
else {//左子树没有
return seekElemNode(T->rchild,x);//搜右子树
}
}
}
//例5:求一棵二叉树的高度
int getBitreehigh(BiTree T) {
if (T == NULL) {
return 0;
}
else {
int lelfhigh = getBitreehigh(T->lchild);
int righthigh = getBitreehigh(T->rchild);
return lelfhigh > righthigh ? lelfhigh + 1 : righthigh + 1;
}
}
//例6:求一棵二叉树中值为x的节点作为根节点的子树的深度
//算法思想就是例4和例5结合,先找到值为x的节点,在根据此节点求二叉树的高度
//例7:交换一棵二叉树的左右子树
void switchLRchild(BiTree T) {
if (T != NULL) {
BiTNode* tmp = T->lchild;
T->lchild = T->rchild;
T->rchild = tmp;
switchLRchild(T->lchild);
switchLRchild(T->rchild);
}
}
//定义三种遍历函数
void Traverse(BiTree T) {
printf("先序遍历结果:");
preorderTraverse(T);
printf("\n");
printf("中序遍历结果:");
inorderTraverse(T);
printf("\n");
printf("后序遍历结果:");
postorderTraverse(T);
printf("\n");
printf("层序遍历结果:");
levelTraverse(T);
printf("\n");
}
//例8:判断两棵树是否相似(长得一样)
bool issimilarBitree(BiTree T1, BiTree T2) {
if (T1 == NULL && T2 == NULL) {
return true;
}
else if (T1 == NULL && T2 != NULL || T1 != NULL && T2 == NULL) {
return false;
}
else {
return issimilarBitree(T1->lchild, T2->lchild) && issimilarBitree(T1->rchild, T2->rchild);
}
}
//例9:判断一棵树是否为完全二叉树
//算法思想:层序遍历树(将空孩子也入队)如果出队的节点为空,是完全二叉树那么队列中的结点都为空,如果有不为空的节点那么就不是完全二
//叉树
bool isCompleteBitree(BiTree T) {
//应用数组模拟队列
BiTNode* Queue[30];//注意这里数组队列的空间
int front = 0;
int rear = 0;
if (T != NULL) {
Queue[++rear] = T;
}
while (front != rear) {//层次遍历
BiTNode* tmp = Queue[++front];
if (tmp == NULL) {//遇到第一个空姐点退出循环
break;
}
Queue[++rear] = tmp->lchild;
Queue[++rear] = tmp->rchild;
}
while (front != rear) {//判断后续节点是否为空
BiTNode *tmp = Queue[++front];
if (tmp != NULL) {//有节点不为空说明不是完全二叉树
return 0;
}
}
return 1;
}
//创建一棵完全二叉树
BiTNode* creatCompleteBitree() {
char pre[7] = { 'A','B','D','E','C','F','G'};//先
char in[7] = { 'D','B','E','A','F','C','G'};//中
return creatBitree1(pre, in, 0, 6, 0, 6);
}
//例10:设计算法利用叶子节点中的的空指针域将所有的叶子节点,链接成一个带头节点的双链表
void Linkleafs(BiTree T, BiTNode*& pTail) {//采用尾插法这样就不用判断插入的节点是否是第一个节点
if (T != NULL) {
if (T->lchild == NULL && T->rchild == NULL) {//叶子节点
T->lchild = pTail;
pTail->rchild = T;
pTail = T;
}
else {
Linkleafs(T->lchild,pTail);//处理左子树
Linkleafs(T->rchild, pTail);//处理右子树
}
}
}
BiTNode* operatFunc(BiTree T) {
BiTNode* L = NULL;
L = (BiTNode*)malloc(sizeof(BiTNode));
assert(L);
L->lchild = NULL;
L->rchild = NULL;
BiTNode* pTail = L;
Linkleafs(T, pTail);
return L;
}
//打印双链表函数(数据类型char)
void print(BiTNode *L) {
BiTNode* p = L->rchild;
while (p) {
printf("%c ", p->data);
p = p->rchild;
}
printf("\n");
}
//例11:一个包含二元运算的算数表达式以二叉链表形式存在在二叉树T中,设计算法求解算数表达式
int compute(char oprt, int leftnum, int rightnum) {//计算函数
switch (oprt) {
case'+':return leftnum + rightnum; break;
case'-':return leftnum - rightnum; break;
case'*':return leftnum * rightnum; break;
case'/':return leftnum / rightnum; break;
}
}
int getnum(BiTree T) {
if (T == NULL) {//树为空
return 0;
}
else if (T->lchild != NULL && T->rchild != NULL) {//操作符节点
char oprt = T->data;
int leftnum = getnum(T->lchild);
int rightnum = getnum(T->rchild);
return compute(oprt, leftnum, rightnum);//递归求值
}
else {//操作树节点
return T->data - '0';
}
}
//创建一棵算数表达式树
BiTNode* creatoprtBitree() {
char pre[7] = { '-','+','2','1','/','4','2' };
char in[7] = { '2','+','1','-','4','/','2' };
return creatBitree1(pre, in, 0, 6, 0, 6);
}
//例12:求一棵二叉树的最大宽度
void getWidthBitree(BiTree T, int level,int wid[],int &max) {
if (T == NULL) return;
wid[level]++;
if (wid[level] > max) max = wid[level];
getWidthBitree(T->lchild, level + 1,wid,max);
getWidthBitree(T->rchild, level + 1,wid,max);
}
int main() {
char pre[5] = { 'A','B','D','C','E' };//先
char in[5] = { 'D','B','A','C','E' };//中
char post[5] = { 'D','B','E','C','A' };//后
char level[5] = { 'A','B','C','D','E' };//层
int prelength = sizeof(pre) / sizeof(pre[0]);
int postlength = sizeof(post) / sizeof(post[0]);
int levellength = sizeof(level) / sizeof(level[0]);
int inlength = sizeof(in) / sizeof(in[0]);
//BiTree T = creatBitree1(pre, in, 0, prelength - 1, 0, inlength - 1);//先序和中序
//BiTree T = creatBitree2(post, in, 0, postlength - 1, 0, inlength - 1);//后序和中序
BiTree T = creatBitree3(level, in, 0, levellength - 1, 0, inlength - 1);//层序和中序
BiTree Ttest = creatBitree3(level, in, 0, levellength - 1, 0, inlength - 1);//层序和中序
Traverse(T);
printf("该二叉树的节点个数为:%d\n", nodesInBitree(T));
printf("该二叉树的叶子节点个数为:%d\n", leafsInBitree(T));
printf("该二叉树的度为1节点个数为:%d\n", getsinglenodes(T));
printf("查找的节点为:%c\n", seekElemNode(T, 'C')->data);
printf("该二叉树的高度为:%d\n", getBitreehigh(T));
printf("以B为根的子树的高度为:%d\n", getBitreehigh(seekElemNode(T, 'B')));
printf("++++++++++++++++++++++++++++++++++++\n");
printf("交换左右子树\n");
printf("交换子树前\n");
Traverse(Ttest);
switchLRchild(Ttest);
printf("交换子树后\n");
Traverse(Ttest);
printf("判断T与Ttest两棵树是否相似(相似返回1,不相似返回0):%d\n", issimilarBitree(T, Ttest));
printf("判断二叉树T是否为一棵完全二叉树(是返回1,不是返回0):%d\n", isCompleteBitree(T));
printf("创建一棵完全二叉树\n");
BiTree TC = creatCompleteBitree();
Traverse(TC);
printf("判断二叉树TC是否为一棵完全二叉树(是返回1,不是返回0):%d\n", isCompleteBitree(TC));
printf("++++++++++++++++++++++++++++++++++++\n");
printf("利用叶子节点中的的空指针域将所有的叶子节点,链接成一个带头节点的双链表\n");
BiTNode* L = operatFunc(TC);
print(L);
printf("++++++++++++++++++++++++++++++++++++\n");
printf("创建一棵算数表达式树\n");
BiTNode* TO = creatoprtBitree();
Traverse(TO);
printf("该算数表达式的值为:%d\n", getnum(TO));
int wid[20] = { 0 };
int max = 0;
getWidthBitree(T, 1,wid,max);
printf("二叉树TC的最大宽度为:%d\n", max);
printf("注意后续不要在使用TC,因为TC已经将叶子节点转变为双链表!!!!!!!!\n");
return 0;
}