Java 数据结构篇-实现 AVL 树的核心方法

news2024/11/22 6:12:16

🔥博客主页： 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍ 

文章目录

        1.0 AVL 树的说明

        2.0 AVL 树的成员变量及其构造方法

        3.0 实现 AVL 树的核心方法

        3.1 获取当前节点的高度 height(AVLNode node)

        3.2 更新当前节点的高度 updateHeight(AVLNode node)

        3.3 平衡因子 bf(AVLNode node)

        3.4 对失衡节点旋转 rotate(AVLNode node)

        3.5 检查节点是否平衡，重新平衡 balance(AVLNode node) 

        3.6 插入、更新节点 put(int key, Object value)

        3.7 删除节点 remove (AVLNode node)

        4.0 实现 AVLTree 核心方法的完整代码

 

        1.0 AVL 树的说明

        AVL树是一种自平衡二叉搜索树，它的名称来源于它的发明者 Adelson-Velsky 和 Landis 。在AVL树中，任何节点的两个子树的高度最多相差 1，这使得AVL树能够保持相对平衡，从而保证了树的查找、插入和删除操作的时间复杂度都是 O(log n) 。

        AVL树的平衡性是通过对节点进行旋转操作来实现的，包括左旋、右旋、左右旋和右左旋。当插入或删除节点后破坏了AVL树的平衡性时，就会进行相应的旋转操作来保持树的平衡。

        也就是说， AVL 树是一种特殊的自平衡二叉搜索树。

        

        2.0 AVL 树的成员变量及其构造方法

        （1）构造 AVLNode 内部类变量 ：

                int key 关键字：通过关键字来比较每个节点的大小。

                Object value 值：通过该变量存放值。

                AVLNode left：引用左孩子节点。

                AVLNode right：引用右孩子节点。

                int height 高度：表示当前节点的高度，默认初始化为 1 。

        （2）AVLNode 内部类构造方法：

                重载两个内部类的构造方法分别为：参数为 key，value 的构造方法、参数为 key，value，left，right 的构造方法。

        （3）构造 AVLTree 外部类 ：

                AVLNode root：表示该树的头节点。

代码如下：

public class AVLTree {

    AVLNode root = null;

    static class AVLNode {
        int key;
        Object value;
        AVLNode left;
        AVLNode right;
        int height = 1;

        public AVLNode(int key, Object value) {
            this.key = key;
            this.value = value;
        }

        public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }

}

        3.0 实现 AVL 树的核心方法

        AVL 树的最核心的方法就是插入、更新、删除操作，因为这些操作都有可能造成二叉搜索树失去平衡。为了解决自平衡的特点，需要每一个插入或者更新、删除操作之后，需要检查是否失去平衡，若失去平衡需要通过左旋、右旋、左右旋、右左旋来重新达到平衡状态；若没有失去平衡，无需任何操作。

        3.1 获取当前节点的高度 height(AVLNode node)

        不能直接通过 node.height 得到当前节点的高度，是因为默认高度为 1，若出现该节点为 null 时，就会出现矛盾，因此需要先判断该节点是否为 null 节点，若为空节点，返回 0 ；若不为 空节点，则返回当前节点 node.height 即可。

代码如下：

    //获取当前节点的高度
    private int height (AVLNode node) {
        return node == null ? 0 : node.height;
    }

 

        3.2 更新当前节点的高度 updateHeight(AVLNode node)

        由于通过删除、插入、旋转都有可能导致当前节点的高度发生改变，所以需要更新高度。实现该方法也很简单，判断当前节点的左右节点的高度，取最大的高度 + 1 就是为当前节点的高度。

代码如下：

    //更新当前的高度
    private void updateHeight (AVLNode node) {
        node.height = Integer.max(height(node.left),height(node.right)) + 1;
    }

        3.3 平衡因子 bf(AVLNode node)

        判断当前节点是否失去平衡，当该节点的左子树的高度 - 右子树的高度 > 1或者 < -1 即失去平衡了。若差值为 1、0、-1，表示没有失去平衡。

代码如下：

    //平衡因子
    private int bf (AVLNode node) {
        return  height(node.left) - height(node.right);
    }

        3.4 对失衡节点旋转 rotate(AVLNode node)

        有四种情况：左旋、右旋、左右旋、右左旋

        左旋：需要先拿到失衡节点 node 的右孩子节点 node.right ,将 r = node.right 赋值给 r 。先将 r.left 赋值给 node.right ，即 node.right = r.left 进行 "换爹" 操作，然后再 "上位" r.left = node 。最后，因为旋转会导致当前 node 的节点与上位后的节点 r 的高度都有可能会改变，所以需要及时更新高度，通过 updateHeight(node)，updateHeight(r)，需要注意的是，更新的顺序不能改变。

        右旋：跟左旋的原理是一样的，需要先拿到失衡节点 node 的左孩子节点 node.left ,将 l = node.left 赋值给 l 。先将 l.right 赋值给 node.left ，即 node.left = l.right 进行 "换爹" 操作，然后再 "上位" l.right = node 。最后，因为旋转会导致当前 node 的节点与上位后的节点 r 的高度都有可能会改变，所以需要及时更新高度，通过 updateHeight(node)，updateHeight(l)，需要注意的是，更新的顺序不能改变。

        左右旋：通过结合左旋、右旋实现左右旋。先拿到当前节点的左节点 l = node.left，对于 l 节点需要用到左旋的方法进行旋转 leftRotate(l)，旋转后需要重新赋值 node.left = leftRotate(l) 。接着对于 node 节点需用用到右旋方法进行旋转 rightRotate(node) 。最后返回 rightRotate(node) 节点即可。

        右左旋：通过结合右旋、左旋实现右左旋。先拿到当前节点的右节点 r = node.right，对于 r 节点需要用到右旋的方法进行旋转 rightRotate(r) ，旋转后需要重新赋值 node.right = rightRotate(r) 。接着对于 node 节点需要用到左旋方法 leftRotate(node) 。最后返回 leftRotate(node) 节点即可。

代码如下：

    //左旋
    private AVLNode leftRotate (AVLNode node) {
        AVLNode r = node.right;
        node.right = r.left;
        r.left = node;
        updateHeight(node);
        updateHeight(r);
        return r;
    }

    //右旋
    private AVLNode rightRotate (AVLNode node) {
        AVLNode l = node.left;
        node.left = l.right;
        l.right = node;
        updateHeight(node);
        updateHeight(l);
        return l;
    }

    //左右旋
    private AVLNode leftRightRotate (AVLNode node) {
        AVLNode l = node.left;
        node.left = leftRotate(l);
        return rightRotate(node);
    }

    //右左旋
    private AVLNode rightLeftRotate (AVLNode node) {
        AVLNode r = node.right;
        node.right = rightRotate(r);
        return leftRotate(node);
    }

        3.5 检查节点是否平衡，重新平衡 balance(AVLNode node) 

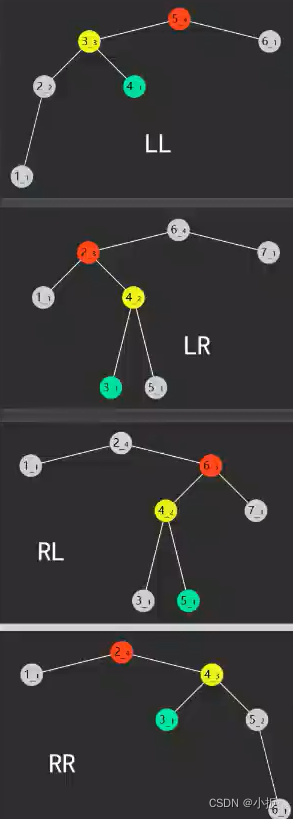
        介绍四种失衡状态的树

        LL : 当前节点 node 的左子树的高度 - 右子树的高度 > 1，且 node.left 的左子树的高度 - node.left 的右子树的高度 >= 0 。实现该情况重新平衡，只需要当前节点进行右旋操作即可。

        LR：当前节点 node 的左子树的高度 - 右子树的高度 > 1，且 node.left 的左子树的高度 - node.left 的右子树的高度 < 0 。实现该情况重新平衡，需要进行先将 node.left 节点进行左旋，重新 node.left = leftRotate(node.left)，接着对于 node 进行右旋即可，也就是上面已经实现的左右旋方法。

        RL：当前节点 node 的左子树的高度 - 右子树的高度 < -1 ，且 node.right 的左子树的高度 - node.right 的右子树的高度 > 0 。实现该情况重新平衡，需要用到上面实现了的右左旋方法。

        RR：当前节点 node 的左子树的高度 - 右子树的高度 < -1 ，且 node.right 的左子树的高度 - node.right 的右子树的高度 <= 0 。实现该情况重新平衡，只需要左旋一次操作即可。

四种失衡状态图：

代码如下：

    //检查节点是否失衡，重新平衡代码
    private AVLNode balance (AVLNode node) {
        if(node == null) {
            return  null;
        }
        if (bf(node) > 1 && bf(node.left) >= 0) {
            return rightRotate(node);
        } else if (bf(node) > 1 && bf(node.left) < 0) {
            return leftRightRotate(node);

        } else if (bf(node) < -1 && bf(node.right) <= 0) {
            return leftRotate(node);

        }else if (bf(node) < -1 && bf(node.right) > 0) {
            return rightLeftRotate(node);
        }
        return node;
    }

        当 node == null 时，返回 null 即可。

        3.6 插入、更新节点 put(int key, Object value)

        使用递归实现插入、更新节点。两种情况，若没有找到 key 关键字时，而找到空位的地方插入新节点；若找到 key 关键字时，更新该节点的值即可。区别于一般的二叉搜索树，自平衡的二叉搜索树，需要在插入节点后更新当前节点的高度和通过旋转来重新达到平衡。需要注意的是，更新节点的操作是不会改变高度还有破坏平衡。

代码如下：

    //更新
    public AVLNode put (int key, Object value) {
        return doPut(root,key,value);
    }

    private AVLNode doPut(AVLNode node, int key, Object value) {
        if (node == null) {
            return new AVLNode(key,value);
        }
        if (node.key == key) {
            node.value = value;
            return node;
        }
        if (node.key > key) {
            node.left = doPut(node.left,key,value);
        }else {
            node.right = doPut(node.right,key,value);
        }
        updateHeight(node);
        return balance(node);
    }

        3.7 删除节点 remove (AVLNode node)

        使用递归实现删除节点思路：

        （1）node == null

        （2）没有找到 key

        （3）找到 key 1) 没有 2）只有一个孩子 3）有两个孩子

        （4）更新高度

        （5）balance

代码如下：

    //删除
    public AVLNode remove (int key) {
        return doRemove(root,key);
    }
    private AVLNode doRemove (AVLNode node,int key) {
        if (node == null) {
            return null;
        }
        if (node.key > key) {
            node.left = doRemove(node.left,key);
        } else if (node.key < key) {
            node.right = doRemove(node.right,key);
        }else {

            if (node.left == null && node.right == null) {
                return null;
            } else if (node.right == null) {
                node = node.left;
            } else if (node.left == null) {
                node = node.right;
            }else {
                AVLNode p = node.right;
                while (p.left != null) {
                    p = p.left;
                }
                p.right = doRemove(node.right,p.key);
                p.left = node.left;
                node = p;
            }
        }
        updateHeight(node);
        return balance(node);
    }

        4.0 实现 AVLTree 核心方法的完整代码

public class AVLTree {

    AVLNode root = null;

    static class AVLNode {
        int key;
        Object value;
        AVLNode left;
        AVLNode right;
        int height = 1;

        public AVLNode(int key, Object value) {
            this.key = key;
            this.value = value;
        }

        public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }


    //获取当前节点的高度
    private int height (AVLNode node) {
        return node == null ? 0 : node.height;
    }

    //更新当前的高度
    private void updateHeight (AVLNode node) {
        node.height = Integer.max(height(node.left),height(node.right)) + 1;
    }

    //平衡因子
    private int bf (AVLNode node) {
        return  height(node.left) - height(node.right);
    }

    //左旋
    private AVLNode leftRotate (AVLNode node) {
        AVLNode r = node.right;
        node.right = r.left;
        r.left = node;
        updateHeight(node);
        updateHeight(r);
        return r;
    }

    //右旋
    private AVLNode rightRotate (AVLNode node) {
        AVLNode l = node.left;
        node.left = l.right;
        l.right = node;
        updateHeight(node);
        updateHeight(l);
        return l;
    }

    //左右旋
    private AVLNode leftRightRotate (AVLNode node) {
        AVLNode l = node.left;
        node.left = leftRotate(l);
        return rightRotate(node);
    }

    //右左旋
    private AVLNode rightLeftRotate (AVLNode node) {
        AVLNode r = node.right;
        node.right = rightRotate(r);
        return leftRotate(node);
    }

    //检查节点是否失衡，重新平衡代码
    private AVLNode balance (AVLNode node) {
        if(node == null) {
            return  null;
        }
        if (bf(node) > 1 && bf(node.left) >= 0) {
            return rightRotate(node);
        } else if (bf(node) > 1 && bf(node.left) < 0) {
            return leftRightRotate(node);

        } else if (bf(node) < -1 && bf(node.right) <= 0) {
            return leftRotate(node);

        }else if (bf(node) < -1 && bf(node.right) > 0) {
            return rightLeftRotate(node);
        }
        return node;
    }

    //更新
    public AVLNode put (int key, Object value) {
        return doPut(root,key,value);
    }

    private AVLNode doPut(AVLNode node, int key, Object value) {
        if (node == null) {
            return new AVLNode(key,value);
        }
        if (node.key == key) {
            node.value = value;
            return node;
        }
        if (node.key > key) {
            node.left = doPut(node.left,key,value);
        }else {
            node.right = doPut(node.right,key,value);
        }
        updateHeight(node);
        return balance(node);
    }

    //删除
    public AVLNode remove (int key) {
        return doRemove(root,key);
    }
    private AVLNode doRemove (AVLNode node,int key) {
        if (node == null) {
            return null;
        }
        if (node.key > key) {
            node.left = doRemove(node.left,key);
        } else if (node.key < key) {
            node.right = doRemove(node.right,key);
        }else {

            if (node.left == null && node.right == null) {
                return null;
            } else if (node.right == null) {
                node = node.left;
            } else if (node.left == null) {
                node = node.right;
            }else {
                AVLNode p = node.right;
                while (p.left != null) {
                    p = p.left;
                }
                p.right = doRemove(node.right,p.key);
                p.left = node.left;
                node = p;
            }
        }
        updateHeight(node);
        return balance(node);
    }
}

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1374440.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[力扣 Hot100]Day2 字母异位词分组

[力扣 Hot100]Day2 字母异位词分组

题目描述 给你一个字符串数组&#xff0c;请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的所有字母得到的一个新单词。 出处 思路 这题有点考阅读理解&#xff0c;意思就是把输入数组中的所含字母相同但顺序不同的单词放到同…
阅读更多...
YOLOv8-Seg改进：轻量化改进 | 超越RepVGG！浙大阿里提出OREPA：在线卷积重参数化

YOLOv8-Seg改进：轻量化改进 | 超越RepVGG！浙大阿里提出OREPA：在线卷积重参数化

🚀🚀🚀本文改进：OREPA在线卷积重参数化巧妙的和YOLOV8结合，并实现轻量化 🚀🚀🚀YOLOv8-seg创新专栏：http://t.csdnimg.cn/KLSdv 学姐带你学习YOLOv8，从入门到创新，轻轻松松搞定科研； 1）手把手教你如何训练YOLOv8-seg； 2）模型创新，提升分割性能； 3）独家…
阅读更多...
创建型模式 | 建造者模式

创建型模式 | 建造者模式

一、建造者模式 1、原理 建造者模式又叫生成器模式&#xff0c;是一种对象的构建模式。它可以将复杂对象的建造过程抽象出来&#xff0c;使这个抽象过程的不同实现方法可以构造出不同表现&#xff08;属性&#xff09;的对象。创建者模式是一步一步创建一个复杂的对象&#xf…
阅读更多...
使用SpringCache操作Redis缓存数据

使用SpringCache操作Redis缓存数据

SpringCache概念 SpringCache是一个框架&#xff0c;实现了基于注解的缓存功能&#xff0c;只需要简单的加一个注解&#xff0c;就能实现缓存功能。 SpringCache提供了一层抽象&#xff0c;底层可以切换不同的缓存实现&#xff0c;例如&#xff1a; EHCacheCaffeineRedis 使…
阅读更多...
vue倒计时60秒改变按钮状态效果demo(整理)

vue倒计时60秒改变按钮状态效果demo(整理)

你可以使用Vue的计时器和绑定状态的方法来实现这个功能。 首先&#xff0c;在data中添加一个计时器countdown&#xff0c;初始值为0。 data() {return {countdown: 0} }<template><div><button click"startCountdown" :disabled"countdown > …
阅读更多...
Android14之解决Pixel手机联网出现感叹号(一百八十)

Android14之解决Pixel手机联网出现感叹号(一百八十)

简介&#xff1a; CSDN博客专家&#xff0c;专注Android/Linux系统&#xff0c;分享多mic语音方案、音视频、编解码等技术&#xff0c;与大家一起成长&#xff01; 优质专栏&#xff1a;Audio工程师进阶系列【原创干货持续更新中……】&#x1f680; 优质专栏&#xff1a;多媒…
阅读更多...
【数据结构】7大排序最详细

【数据结构】7大排序最详细

0.前言 接下来进入排序&#xff0c;我们知道在c语言阶段可能就学习过了像冒泡排序&#xff0c;选择排序这种比较简单的排序&#xff0c;那么接下来我们就会学习到更加高级的排序算法。但高级代表着难度的提升&#xff0c;但不用担心&#xff0c;博主会细细来谈&#xff0c;慢慢…
阅读更多...
九州金榜如何高质量培养孩子成长

九州金榜如何高质量培养孩子成长

在这个时代&#xff0c;孩子们就像温室里的花朵&#xff0c;被父母和家人宠爱着&#xff0c;享受着最优越的物质条件。 然而&#xff0c;在这样的环境中成长起来的孩子&#xff0c;却往往被很多父母称为"白眼狼"&#xff0c;对孩子的自私行为感到痛苦和失落。 1 随…
阅读更多...
zookerper入门

zookerper入门

zookerper介绍 ZooKeeper 是一个开源的分布式协调框架,主要用来解决分布式集群中应用系统的一致性问题. ZooKeeper本质上是一个分布式的小文件存储系统&#xff08;Zookeeper文件系统监听机制&#xff09;.提供基于类似于文件系统的目录树方式的数据存储&#xff0c;并且可以…
阅读更多...
离线安装telnet-server

离线安装telnet-server

telnet下载地址&#xff1a; https://vault.centos.org/ 需要下载telnet 和 telnet-server 确认自己的服务器版本&#xff0c;我这里使用的是&#xff08;Red Hat Enterprise Linux Server release 7.0 (Maipo)&#xff09;对应的是Centos 7.0,所有到 https://vault.centos.or…
阅读更多...
HarmonyOS应用开发学习笔记 UI布局学习 创建轮播（Swiper） artTS 轮播组件 简单使用

HarmonyOS应用开发学习笔记 UI布局学习 创建轮播（Swiper） artTS 轮播组件 简单使用

官方文档 Swiper组件提供滑动轮播显示的能力。Swiper本身是一个容器组件&#xff0c;当设置了多个子组件后&#xff0c;可以对这些子组件进行轮播显示。通常&#xff0c;在一些应用首页显示推荐的内容时&#xff0c;需要用到轮播显示的能力。 1、简单用法 loop 控制是否循环 …
阅读更多...
AI交互数字人如何助力职工之家数字化建设？

AI交互数字人如何助力职工之家数字化建设？

近日&#xff0c;广州市海珠区产投园区工友之家揭牌&#xff0c;首批“工会数字人”正式揭幕亮相&#xff0c;开启24小时零距离全天候服务职工模式。同步进驻海珠区10个产业园区的其他工会数字人也进入全天候服务状态&#xff0c;职工群众可“一码入会”&#xff0c;工会数字人…
阅读更多...
非常好用的个人工作学习记事本Obsidian

非常好用的个人工作学习记事本Obsidian

现在记事本有两大流派&#xff1a;Obsidian 和Notion&#xff0c;同时据说logseq也很不错 由于在FreeBSD下后两种都没有相关ports&#xff0c;所以优先尝试使用Obsidian Obsidian简介 Obsidian是基于Markdown文件的本地知识管理软件&#xff0c;并且开发者承诺Obsidian对于个…
阅读更多...
【算法每日一练]-动态规划 （保姆级教程 篇16) #纸带 #围栏木桩 #四柱河内塔

【算法每日一练]-动态规划 （保姆级教程 篇16) #纸带 #围栏木桩 #四柱河内塔

目录 今日知识点&#xff1a; 计算最长子序列的方案个数&#xff0c;类似最短路径个数问题 四柱河内塔问题&#xff1a;dp[i]min{ (p[i-k]f[k])dp[i-k] } 纸带 围栏木桩 四柱河内塔 纸带 思路&#xff1a; 我们先设置dp[i]表示从i到n的方案数。 那么减法操作中&#xff…
阅读更多...
Linux-shell简单学习

Linux-shell简单学习

我是南城余&#xff01;阿里云开发者平台专家博士证书获得者&#xff01; 欢迎关注我的博客&#xff01;一同成长&#xff01; 一名从事运维开发的worker&#xff0c;记录分享学习。 专注于AI&#xff0c;运维开发&#xff0c;windows Linux 系统领域的分享&#xff01; 其他…
阅读更多...
学习c语言，强制转换

学习c语言，强制转换

因为sizeof是无符号数所以-1会转换成无符号数&#xff0c;所以答案是i大于sizeof的
阅读更多...
权限维持篇

权限维持篇

一、Windows 1、 不死马权限维持 1.1 概述 <?php ignore_user_abort(); //关掉浏览器&#xff0c;PHP脚本也可以继续执行. set_time_limit(0);//通过set_time_limit(0)可以让程序无限制的执行下去 $interval 5; // 每隔*秒运行 do { $filename test.php; if(file_exi…
阅读更多...
Mysql——索引相关的数据结构

Mysql——索引相关的数据结构

索引 引入 我们知道&#xff0c;数据库查询是数据库的最主要功能之一。我们都希望查询数据的速度能尽可能的快&#xff0c;因此数据库系统的设计者会从查询算法的角度进行优化。最基本的查询算法当然是顺序查找&#xff08;linear search&#xff09;&#xff0c;这种复杂度为…
阅读更多...
C# FreeSql使用，基于Sqlite的DB Frist和Code First测试

C# FreeSql使用，基于Sqlite的DB Frist和Code First测试

文章目录 前言FreeSql 简单连接数据库服务不存在没装FreeSql.All装了FreeSql.All安装包选择 DBFirst安装命令行生成器生成Bat创建脚本 基于Sqlite的Code Frist文件夹自动导出到Debug目录Sqlite 数据库安装和创建Sqlite连接数据库自动增列增表测试增列删列改列名同名列改属性 Co…
阅读更多...
【小黑嵌入式系统第十四课】μC/OS-III程序设计基础（三）——信号量（任务同步资源同步）、事件标记组（与或多个任务）

【小黑嵌入式系统第十四课】μC/OS-III程序设计基础（三）——信号量（任务同步资源同步）、事件标记组（与或多个任务）

上一课&#xff1a; 【小黑嵌入式系统第十三课】PSoC 5LP第二个实验——中断控制实验 前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。点击跳转到网站&#xff1a;人工智能 文章目录 1 信号量1.1 简介1.2…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023