信道编码理论【信息论安全】

news2024/12/24 3:32:04

一. 信道编码模型

二. 信道编码速率与错误译码率

2.1 信道编码速率

2.2 平均错误率

三. 信道容量

四. 小结

一. 信道编码模型

（1）消息

假定消息集合为M，如下：

$M=[1,2^{nR}]$

（2）编码

将消息m映射成码字 $x^n$ ，该码字的长度为n，可以通过编码函数实现，如下：

$f:M\to X^n$

（3）译码

信道的输出长度与输入长度相等，均为n。将输出的 $y^n$ 可以译码成 $\hat m\in M$ ，也可能译码错误为“？”。此过程可通过译码函数g实现，如下：

$g:y^n\to M\cup \lbrace ?\rbrace$

要求信道的传输过程为离散无记忆信道，如下：

$DMC(X,p_{Y|X},Y)$

以上过程即为信道编码（channel code） $C_n$ ，重要的参数包含 $(2^{nR},n)$ 。形式化的完整定义如下：

二. 信道编码速率与错误译码率

2.1 信道编码速率

可以设计不同的编码函数，从而形成不同的码本（codebook），如下：

$\lbrace f(m):m\in [1,2^{nR}]\rbrace$

通常而言会假定消息空间M是均匀随机分布的，由此信道编码速率其实就是R。因为信道编码的目的是加冗余，在网络安全模型中，该R的值一般为小于1的数。当然，考虑到会有小数的情况出现，所以完整的信道编码速率为：

$\frac{1}{n}log\lceil 2^{nR}\rceil$

信道编码速率的单位是bit/channel use。

2.2 平均错误率

当译码的 $\hat M$ 和编码的M不同时，则出现了错误译码。由此定义平均错误概率为：

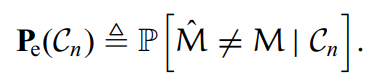
其中 $C_n$ 代表会公开所有编码和译码的理论依据， $P_e$ 代表错误概率。所以该概率写成了条件概率的形式。

三. 信道容量

信道可达的速率要求，当编码长度足够大时，错误译码的概率需要接近于0，也就是：

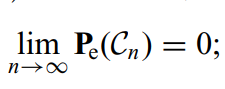
相当于当编码长度越来越大时，方案错误率越来越低，但是方案的效率也会越来越低。很明显，满足可达速率的方案有很多，那么最大的速率可以达到多少呢？

当速率达到最大值时，就出现了信道容量（channel capacity）的概念，如下：

其中sup代表可达的上界。

在无线通信中，信息论只依赖于给定的概率分布，因为求的是可达速率的上界，所以跟编码的长度n或k都没有关系。

如果某个编码方案可以实现信道容量的话，则被称之为direct result，相应的证明过程则被称之为achievability proof。

当有定义证明没有编码方案可以实现信道容量的话，则被称之为converse result，相应的证明过程则被称之为converse proof。

这就是所谓的编码定理。当年香农是这样总结的：

Notice that the formulation of the point-to-point communication problem does not put any constraints either on the computational complexity or on the delay of the encoding and decoding procedures. In other words, the goal is to describe the fundamental limits of communications systems irrespective of their technological limitations.

四. 小结

通信技术发展日新月异，使我们的社会变成为一个万物互联的社会。目前已有超过 500 亿台通信连接设备，它们在医疗保健、自动驾驶、制造业、农业、航运和娱乐等行业中发挥着巨大的作用。预测2035 年全世界经济收益总产出实现 12.3 万亿美金， 2036 年，通讯经营公司将会在全世界雇佣 2200 万务工人员。 5G 就是其中一个例子，它目前有三个不同的应用：

（1） eMBB-加强移动信号宽带；

（2） URLLC-超安全可靠的低延迟作用通讯；

（3） mMTC-大型机器种类通讯。

这三个使用都有不同的要求，从 eMBB 的高达 10Gbps 的速率到 URLLC 少于 10e-5 丢包，以及通过 mMTC 设想的超过500 亿个低功耗设备。

现代数字通信的核心之一是信道编码，或者也称为前向纠错（ Forward Error Correction,FEC），根据未来通信系统的条件，信道编码还必须满足如高速率、超高可靠性以及低功耗等要求。信道编码领域自诞生之日起就对社会产生了深远影响。在 70 年代末， Ungerboeck 指出了协同调节控制和程序代码设计方案—格子程序代码调节控制（Trellis-Coded Modulation）。这个方案能够将普通电话线上的调制解调器的吞吐量从 23kbps 提高到 45kbps。

Arikan 在 2009 年第一次提出了极化码，而且在理论上充分证实了极化码在二进制输入对称离散无记忆信道下，就能够“实现”香农容量，这对于我们实现大容量通信传输的信道编解码技术有重要意义，并且极化码的编译码算法都具备较低的复杂度，性能在特定码长下也非常优秀。然而在实际的应用中，传输信道的状态在变化，为了适应这种变化，我们就需要对极化码的码长、码率等参数进行灵活调整。

第五代移动通信对通信传输的高品质要求，决定了其对于高速率、高可靠、低时延的译码器的需求。对于极化码，即使传统类型的译码算法及改善过的算法都具备了非常好的译码性能，例如 SC 译码算法及其改进译码算法，然而在译码时延上受制于译码算法本身，需要在低时延上继续获得突破。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1374210.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！