4.1关系的概念

1)序偶及n元有序组

由两个个体x和y，按照一定顺序排序成的、有序数组称为有序偶或有序对、二元有序组，

记作<x，y>，其中x是第一分量，y是第二分量。

相等有序偶：第一分量和第二分量分别相等。

三元有序组：也是一个有序偶，<<x,y>,z> 其中第一分量是一个有序偶。

（注意：<x,<y,y>>不是一个三元有序偶，只能第一分量作为有序偶。）

一般的，n元有序偶的第一分量为n-1元有序偶，第二分量为单独的分量。（举个例子，5元有序偶的第一分量有4个，第二分量只有一个）

2)笛卡尔积/直积

  给定集合A和集合B，若有序偶的第一分量属于集合A，第二份量属于集合B。这样的有序偶的集合叫做集合A和集合B的笛卡尔积或直积、叉积，记作A✖B。

约定：若A是空集，或者B是空集，那么A✖B也是空集。

若A、B是有限集合，则|A×B| = |A| |B|

一般的，笛卡尔积不满足交换律，即A✖B  ！= B✖A

笛卡尔积运算对集合并运算U和集合交运算n具有分配律。

A✖（B U C） = A ✖B U  A✖C

A的n节笛卡尔积记作A^n，A^n = A ✖ A ✖A ...✖A

一般的，若A1，A2，A3...An都是有限集合，则|A1 ✖ A2 ✖ ...An| = |A1| |A2|... |An|

3)二元关系的基本概念

  定义：任意一个有序偶的集合称为一个二元关系，记作R。如果<x,y>属于R，那么就称x和y有关系R，记作xRy。反之，就是x和y没有关系R。

设X和Y是集合，X✖Y的任意子集R称为X到Y的二元关系。记作R：X->Y。

特别的，当X = Y时，称R为X上的二元关系。

（X✖Y在前面的有序偶我们学习过，就是以X的元素为第一分量，以Y的元素作为第二份量组成的一个有序偶<x，y>的集合，也叫做笛卡尔积。X✖Y的结果是一个二元有序偶的集合）

设R是二元关系，称domR为R的定义域（也就是集合X），称ranR为R的值域（也就是集合Y）。

定义域domR和值域ranR一起称为R的域，记作FLDR。

若|X| =m，|Y| = n，则|X × Y| = mn，X×Y的不同子集共有2^mn个，于是从X到Y的二元关系共有2^mn个。（这里，要怎么理解？要记住，R本质上也是一个关系的集合，也就是X和Y中有关系R的元素的集合，而这个关系R可以是很多种）

注意：设X和Y是集合，则

1）空集是X×Y的子集，称为X到Y的空关系

2）X×Y称X到Y的痊愈关系

3）{<x,x> |x属于X}称为X上的恒等关系，记作Ix。

4）二元关系的表示

有限集合的二元关系是一种集合，可以用集合的方法表示。

有三种表示方法：图示法、关系矩阵法、关系图法。

1）图示法

用大圆圈表示集合X和集合Y，放在两边，用小圆圈表示X和Y种所有的元素，旁边写上相应的元素名，有关系就用有方向的弧线连接起来。从第一分量指向第二分量。

2）关系矩阵法

3）关系图法

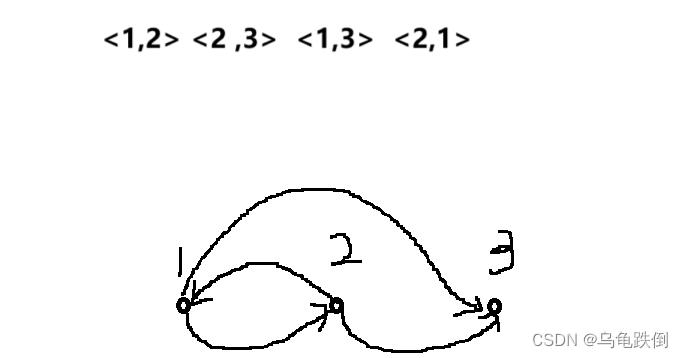
4.2关系的性质

主要的关系有自反性、反自反性、对称性、反对称性和传递性。

自反：对所有的元素x,都有<x,x>

反自反：多有的有序对不能有任何一个<x,x>

对称：对所有的x和y,只要有<x,y>就有<y,x>

反对称：一个对称都不能有

传递：对所有的<x,y>,必有<y,z>

4.3关系的运算

逆关系：即所有的有序对交换位置：<x,y> 的逆关系就是<y,x>

复合关系：通俗理解来说，一个二元关系R<x,y>和另一个二元关系S<y,z>做复合运算，将二元关系视作为某种运算或者说操作，通过二元关系R是的x得到y，再通过二元关系S是的y得到z。所以，从这个角度来理解，一般计算二元关系都是使用关系矩阵来实现这种从x到y到z的变换，即使R和S的复合计算即两个关系矩阵的相乘的结果。

关系的幂运算：通俗来说，假设有一个二元关系R，对于其关系图来说，一次幂就是点与点之间只走一步，2次幂就是点与点之间走两步，3次幂就是点与点之间走三步，以此类推。

4.4关系的闭包运算

自反闭包的计算：有一个二元关系R，其自反闭包r（R）等于其恒等关系并上R，恒等关系就是R中所有元素的自反，即<x,x>、<y,y>等。

对称闭包的运算：有一个二元关系R，其对称闭包等于R并上其逆关系（<x,y>的逆关系为<y,x>即二元有序对交换位置）。这很好理解，两个关系矩阵做布尔加法即可，对角线的两边对称。

传递闭包的运算：这个比较复杂，一般的计算方法是，R的传递闭包t（R）等于其关系矩阵的1次幂、2次幂....直到n次幂的矩阵做矩阵相加，得到的最终矩阵即传递闭包。

4.5等价关系与等价类

等价关系：自反、对称、传递。

什么叫做等价？若R是等价关系，其有序对<x,y>称为x等价于y。

等价类：是元素的集合，这个集合内的所有元素都是等价的，只要满足这一条件的都叫做等价类。

商集：R是一个等价关系，其所有元素的集合就是商集，记作A/R

4.6相容关系与相容类

相容关系：自反、对称

相容类：有一个定义在A上的相容关系r，对于任何属于A这个集合的任意两个元素有a1 r a2，即使他们之间构成相容关系，那么其就构成一个相容类。和等价类一样，都是元素的集合，而这个集合的元素都满足这个相容关系。

总结来说就是，等价类和相容类都是元素的集合，而这个元素都有等价的关系或者相容的关系。

4.7序关系与哈塞图

偏序关系：自反、反对称、传递

哈塞图：哈塞图是偏序关系的延申，通俗来说，有一个偏序关系r，有<x,y>必有<y,z>，对于构成的<x,z>，中间再没有其他关系例如<y,w><w,z>。

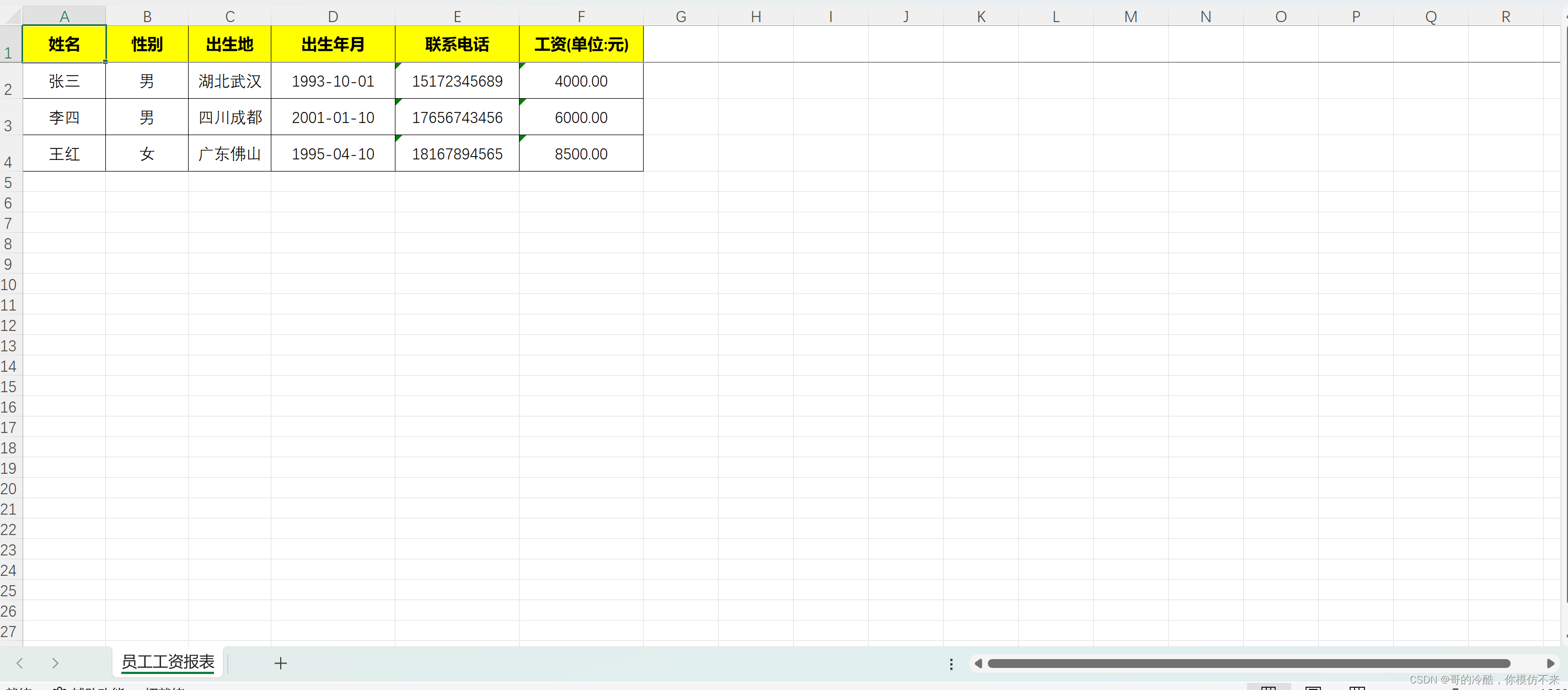
哈塞图：

以上图为例：

极大元：4

极小元：27，12，24

最大元：4

最小元：没有极小元

（注意：不论是最大还是最小元，都必须能和所有的其他元素能对比，即有路径，这很好理解，即既然都不能和所有的元素对比，那么有没有大小之分，而这很明显不符合最大或者最小的要求）
上界：对于一个哈塞图A，求比B的上确界，那么比B的所有元素大的元素的集合就是上界

下界：对于一个哈塞图A，求比B的上确界，那么比B的所有元素小的元素的集合就是下界

上确界：上界的最小值，很好理解，即从这个点开始以上都是上界

下确界：下界的最大值，也很好理解，即从这个点开始以下都是下届