文章目录
- 数据结构期末复习
- 第一章:数据结构绪论
- 第二章:顺序表与单链表
- 第三章:其它链表
- 第四章:栈
- 如何中缀转后缀
- 后缀如何计算
- 第五章:队列
- 第六章:串
- 第七章:树的概念和遍历
- 第八章:赫夫曼树编码
- 第九章:图
- 第十章:查找与排序
数据结构期末复习
第一章:数据结构绪论
- 时间复杂度是衡量算法好坏的一个最重要的标准
- 数据结构是为了在解决问题时让处理过程实现空间与时间上的最优
第二章:顺序表与单链表
- 线性表: n个数据元素的有限序列
- 线性表顺序表示: 用一组地址连续的存储单元依次存储线性表的数据元素
- 随机存取
- 增删时需要移动大量元素
- 线性表链式表示:存储单元并不连续,通过指针等手段来表示数据之间的邻接关系
- 不可随机存取
- 增删时只需要修改前后节点
第三章:其它链表
- 双向链表:使用 prior 和 next 指针表示邻接关系(我平时一般用的 prev)
- 链表的优缺点:
- 缺点:无法进行随机存取
- 优点:相较于顺序表,能够更快得进行增删操作
第四章:栈
-
栈:先进后出
- 只在 top 端进行数据进栈与出栈的操作
-
栈的应用:
- 表达式的计算:先将中缀转后缀,再使用后缀进行计算
- 递归算法
如何中缀转后缀
- 中缀转后缀的核心要点是
- 遇到数字直接写入后缀表达式
- 遇到左括号直接入栈(左括号的优先级 = 空栈)
- 遇到操作符
- 如果栈为空直接入栈
- 该操作符的优先级大于栈顶操作符就入栈,如果小于等于就让栈顶出栈,并写入后缀表达式,直到可以入栈为止
- 如果遇到右括号就直接让栈顶出栈,写入后缀表达式,直到遇到左括号出栈结束
- 最后结尾依次出栈即可
举个例子,中缀表达式:2 * ( 3 + 5 ) + 7 / 1 - 4 转后缀
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2
栈:空
(数字直接写入后缀)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2
栈:*
(栈空直接入栈)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2
栈: (*
(左括号直接入栈)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3
栈: (*
(数字直接写入后缀)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3
栈: ( +*
(左括号 = 空栈,空栈直接入栈)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3 5
栈: ( +*
(数字直接写入后缀)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3 5 +
栈:*
(操作符出栈写入后缀,直到左括号)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
**后缀:2 3 5 + ***
栈:+
(操作符优先级小于等于栈顶,出栈写入;而后栈为空,操作符入栈)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3 5 + * 7
栈:+
(数字直接写入后缀)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3 5 + * 7
栈:+ /
(操作符优先级大于栈顶,直接入栈)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3 5 + * 7 1
栈:+ /
(数字直接写入后缀)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3 5 + * 7 1 / +
栈:-
(操作符优先级小于等于栈顶,出栈写入;而后栈为空,操作符入栈)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3 5 + * 7 1 / + 4
栈:-
(数字直接写入后缀)
中缀:2 * ( 3 + 5 ) + 7 / 1 - 4
后缀:2 3 5 + * 7 1 / + 4 -
(结尾依次出栈即可)
后缀如何计算
后缀的计算很简单,让数字不断入栈,遇到操作符就从栈中取两个数字计算,再让计算结果重新入栈,循环往复即可
第五章:队列
-
队列:先进先出
- 只在队尾端进行数据进队,只在队首进行数据出队
-
队列的种类:
- 顺序表示:使用简单但数组容易溢出
- 链表表示:保留 front 和 rear 两个指针
- 循环顺序表示:
- front == rear 时为空
- ((rear + 1) % MAXQSIZE == front 时为满
-
队列的应用:
- 活用先进先出特点
第六章:串
- 串:字符串
- 成员类型为 char 类型的线性表
- 串的模式匹配
- 查找子串在主串中出现的位置
- 穷举法: O(nm)
- KMP 算法
- next 矩阵记录子串的跳转信息
- 活用以匹配的信息进行查找
- 时间复杂度: O(n+m)
KMP 算法
例题:模式串 p = “abcabx” 的 next 函数值序列为(以第一个字母序号为 “1” 计算)___
使用方法:最简单通俗易懂求 next 数组的方法 - CSDN 博客
0 a
0 ab
0 abc
1 abca
2 abcab
0 abcabx
分别计算每一层的最大前缀;在前面加一个 0,删去最后一个数,剩下的数全部 + 1 即可。
最终求的:0 1 1 1 2 3
第七章:树的概念和遍历
重要概念:
- 结点:包含一个数据元素及若干指向其子树的分支
- 分支:结点之间的连接
- 结点的度:结点拥有的子树数
- 树的度:树中结点度的最大值称为树的度
- 叶子结点:度为 0 的结点就是没有子树的结点
- 分支结点:度不为 0 的结点包括根结点,也称为非终端结点。除根外称为内部结点
- 层次:根结点为第一层,其孩子为第二层,依此类推
- 深度:树中结点的最大层次
解释一下什么是结点的度:
比如说一个节点没有孩子,他的度为 0;有一个孩子,度为 1;有两个孩子,度为 2。
树的度,看的是整棵树所有的节点,取其中度最大的节点作为树的度。
来看看二叉树的经典问题:
一棵有 124 个叶结点的完全二叉树最多有___个结点
解析:
1、根据二叉树的性质 叶子节点数 = 度为 2 的节点 + 1,因此度为 2 的结点数为 124 -1 = 123
2、而完全二叉树中度为 1 的结点数最多 1 个。
3、因此该完全二叉最多有:124+123+1 = 248 个结点。
深度为 5 的二叉树,其结点数最多为___个
2^(n-1)-1 = 31
当二叉树采用完全二叉树进行存储时(编号从 1 开始),其双亲编号为 k,则其右孩子编号为___
2k+1
第八章:赫夫曼树编码
根据使用频率,5 个字符的赫夫曼编码不可能是(C)
A. 111,110,10,01,00
B. 000,001,010,011,1
C. 100,11,10,1,0
D. 001,000,01,11,10
解析:
画图,1 往右,0 往左
设给定权值总数有 n 个(权值总数为待编码的字符数,也就是赫夫曼树的叶子结点数),其赫夫曼树的结点总数为(A)
A. 2n-1
B. 2n
C. 2n+1
D. 不能确定
解析:
现场画一棵树推导一下

解析:
通过权值画图(这里权值截图截漏了)
(2)求其加权路径长度 WPL
解析:
将所有节点的权值*深度加在一起就是 WPL
(3)写出每个字符对应的赫夫曼编码
解析:
根据赫夫曼树向左为 0,向右为 1 求出每个字符的编码
第九章:图
以下说法中正确的是(C)
A. 连通分量是无向图中的极小连通子图
B. 有向图的遍历不可采用广度优先搜索方法
C. 连通图的生成树包含了图中所有顶点
D. 对 n 个顶点的连通图 G 来说,如果其中的某个子图有 n 个顶点和 n-1 条边,则该子图一定是 G 的生成树
解析:
A:
连通分量是图中的极大连通子图
B:
肯定可以用
D:
生成树具有连通图的全部 n 个顶点和连接它们的 n-1 条边。
如果它的一个子图有 n 个结点,也有 n-1 条边,但它们没有连接所有顶点,有的地方还出现了回路,则此子图不是生成树。
设图有 n 个顶点和 e 条边:
(1)采用邻接矩阵时,遍历图的顶点所需时间为___
(2)采用邻接表时,遍历图的顶点所需时间为___
解析:
(1)O(N^2)
(2)O(N+e)
设 G 是一个非连通无向图,有 15 条边,则该图至少有___个顶点
解析:
13
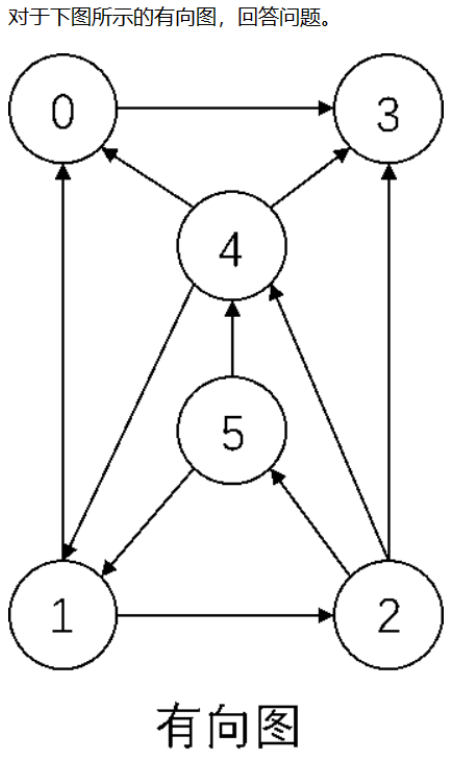
(1)邻接矩阵,用表格表示
解析:
二维表格,谁(x)指向谁(y),就是(x,y)
(2)强连通分量,分别写出顶点的集合、连接这些顶点的所有弧的集合
解析:
强连通分量就是:A 节点能到 B 节点,B 节点也能到 A 节点
(3)从顶点 0 出发进行深度优先遍历序列
解析:
从 0 开始遍历每一个节点,visit
(4)从顶点 2 出发进行广度优先遍历序列
解析:
将没有走过的节点都入队列,走过的节点再次遇到就跳过
第十章:查找与排序
- 查找
- 查找简单的比较简单,难的又很难,战略放弃这部分:
- 静态查找、二叉搜索树、二叉平衡树、B 数、哈希查找
- 排序
- 各种经典排序,主要了解:
- 希尔排序、快速排序、堆排序、归并排序、基数排序