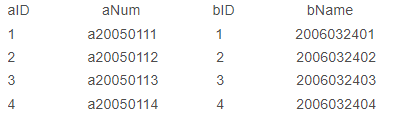目录
今日知识点:
二维图形的状态压缩,存下所有的合法状态然后暴力遍历
dfs的优化剪枝
二项式定理
俄罗斯方块
ABC Puzzle
lnc的工资
俄罗斯方块
322D
题意:在4*4方格中分别给出3个俄罗斯方块,问是否可以经过旋转,平移操作恰好拼满整个4*4格子? 不能重叠和越界。
输入样例:
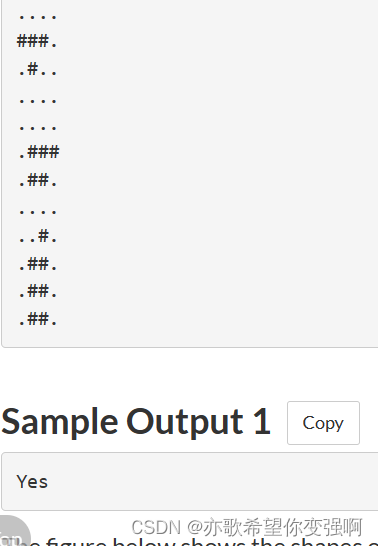
样例解释

思路:
首先是如何存储图形以及变化后的图形,当然不仅要方便变换还要方便最后检查。然后就想到了状态压缩,一共最多16格子,最多需要16位就行。
也就是最大用2^16-1的数字即可表示这种状态,然后对3个俄罗斯方块一一组合遍历看看能否最4*4方格进行平铺。
如何存入状态:4*4每个格子一一对应1~16的位置,有效的格子坐标转换到一维的二进制位置进行更新。(1<<?和二进制数字相或)平移操作就是把所有位置移动一下。旋转不过是对原字符串进行适当变化,然后把所有的变换后的有效状态存下来。
如何遍历结果:将3个状态数字相或,然后看是否全是1即可,判断是否等于1<<(4*4)-1就行
要注意不能有重叠:任意两个状态数字不能相与必须为0
非常好的一道状态压缩题!!!
#include <bits/stdc++.h>
using namespace std;
const int SIZE=4;
void rotate(string s[]){//旋转函数(顺时针旋转)
char tmp[SIZE][SIZE];
for(int i=0;i<SIZE;i++){
for(int j=0;j<SIZE;j++){
tmp[j][SIZE-1-i]=s[i][j];//i为0时:tmp[0,1,2][2]=s[0][0,1,2]
}//相当于横着的变成竖着的
}
for(int i=0;i<SIZE;i++){
s[i]=string (tmp[i],tmp[i]+SIZE);//string函数:从第一个字符位置开始转换,长度位SIZE
}
}
bool valid(int x){return x>=0&&x<SIZE;}
int get(string s[],int dx,int dy){
int ret=0;
for(int x=0;x<SIZE;x++){
for(int y=0;y<SIZE;y++){
if(s[x][y]=='#'){
int xx=x+dx,yy=y+dy;
if(!valid(xx)||!valid(yy)){//不能越界,函数重用嘛
return -1;
}
ret |=1<<(xx*4+yy);//xx*4+yy是把每个对应格子给算成数字,然后和ret或运算修改对应位置(有1出1)
}
}
}
return ret;
}
vector<int>add(){
vector<int>ret;//用于存放状态
string s[SIZE];
for(int i=0;i<SIZE;i++)cin>>s[i];//输入字符阵列
for(int num=0;num<4;num++){//执行四个旋转操作
for(int dx=-3;dx<=3;dx++){//执行平移操作,要注意的是不仅要向右平移,还要向左平移
for(int dy=-3;dy<=3;dy++){//向上和下平移
int v=get(s,dx,dy);//用一个数字来存下次时旋转和平移后的结果(1~16个1的状态,只需要16位即可最多2^16-1)
if(v>=0){ret.push_back(v);
}
}
}
rotate(s);//旋转一下
}
return ret;//返回这个俄罗斯方块对应的全部状态
}
int main(){
vector<int>mask[3];
for(int id=0;id<3;id++){
mask[id]=add();//输入字符阵列,获取四个方向,所有平移结果的状态数字,存入mask中
}
for(int x:mask[0]){//检查所有的情况有没有能成立的
for(int y:mask[1]){
for(int z:mask[2]){
if((x|y|z)+1!=(1<<SIZE*SIZE))continue;//x|y|z就可以把1的位置全部标出来(要等于2^16-1嘛)
if(x&y)continue;
if(x&z)continue;
if(z&y)continue;
cout<<"Yes\n";
return 0;
}
}
}
cout<<"No\n";
}
ABC Puzzle
326D
题意:给两个长n的仅由ABC组成的字符串s1,s2,是否在n*n阵列中满足以下条件,若满足则输出,不满足输出No
条件1:每行每列仅包含一个A,一个B,一个C (3<=n<=5)
条件2:第i行最左边的字符恰好是s1的第i个字符
条件3:第i列最上边的字符恰好是s2的第i个字符
输入样例: 输出样例:
5 Yes
ABCBC AC..B
ACAAB .BA.C
C.BA.
BA.C.
..CBA
思路:
一道比较恶心的dfs题。
说一下dfs思路吧:
依次放每个格子可以放. 也可以放A或B或C这四种选择。然后全部放完就检查一下即可。因为走错就要回溯,这最大妥妥的4^25根本过不去。首先主要到每行每列最多两个. 那么就要加以剪枝。
设置cnt[0][i][?]表示第i行已经有几个. 字符,cnt[1][i][?]对应第i列已经有几个. 字符?(剪枝1)
if(cnt[0][x]['.']<n-3&&cnt[1][y]['.']<n-3){//这是放"."的情况,每行列最多放两个,因为只放一次,所以if语句即可
an[x][y]='.';
cnt[0][x]['.']++;cnt[1][y]['.']++;
dfs(x,y+1);
cnt[0][x]['.']--;cnt[1][y]['.']--;
}然后是放置3种字母。首先是看看同行是否已经有该字符。同样设置cnt[0][x][c]代表第x行是否有该字符,cnt[1][y][c]代表第y行是否有该字符。(剪枝2)
接着是看是否和原字符串的对应位置匹配。第一个字符串对应x行,第二个字符串对应y列,我们如果swap后如果传入的是s[0][x]是0,那么自动返回1,这种情况就对应已经有了开头字符了。如果没有开头字符那就直接和开头字符比较看是否相同。(剪枝3)
for(char c='A';c<='C';c++){//放3种字母
if(cnt[0][x][c]==0&&cnt[1][y][c]==0){//第x行y列是否都没有该字符
if(match(s[0][x],c)&&match(s[1][y],c)){
//开头都确定,开头一个确定另一个不确定但相等,开头都不确定但都相等
an[x][y]=c;
char tmp=0,tmp2=0;
swap(tmp,s[0][x]);//0和0交换(开头已经确定),0和非0交换(开头未确定变已确定)
swap(tmp2,s[1][y]);
cnt[0][x][c]++;cnt[1][y][c]++;
dfs(x,y+1);
cnt[1][y][c]--;cnt[0][x][c]--;//失败,回溯(回溯尽量去swap,这样更容易恢复状态)
swap(tmp,s[0][x]);//交换回来
swap(tmp2,s[1][y]);
}
}
}好了,经过以上的剪枝,这个dfs就能过去了
#include <bits/stdc++.h>
using namespace std;
int n;
int cnt[2][5][128];//cnt[0][i][?]表示第i行已经有几个?字符(ASCII),cnt[1][i][?]对应相关列
char an[5][7];//答案阵列
string s[2];
bool match(char c1,char c2){
if(!c1)return 1;//如果说传过来的s[0,1][?]对应第?行,列已经有开头字符了(将会传过来0),那就直接返回正确
return c1==c2;//否则就去比较这两个字符
}
//void型dfs 中return其实可有可无,其实就相当于是函数的continue功能,是为了防止进入走后面的代码,引发错误!
//dfs中的标记变量,一定要设置为局部变量,避免被别的dfs给修改
void dfs(int x,int y){//其实每个格子都有4种选择,不见得非ABC就要回溯,一定要细心
if(x==n){
cout<<"Yes\n";
for(int i=0;i<n;i++)cout<<an[i]<<'\n';
exit(0);//任务完全直接结束
}
if(y==n){dfs(x+1,0);return ;}
if(cnt[0][x]['.']<n-3&&cnt[1][y]['.']<n-3){//这是放"."的情况,每行列最多放两个,因为只放一次,所以if语句即可
an[x][y]='.';
cnt[0][x]['.']++;cnt[1][y]['.']++;
dfs(x,y+1);
cnt[0][x]['.']--;cnt[1][y]['.']--;
}
for(char c='A';c<='C';c++){、、放3种字母
if(cnt[0][x][c]==0&&cnt[1][y][c]==0){//第x行y列是否都没有该字符
if(match(s[0][x],c)&&match(s[1][y],c)){
//开头都确定,开头一个确定另一个不确定但相等,开头都不确定但都相等
an[x][y]=c;
char tmp=0,tmp2=0;
swap(tmp,s[0][x]);//0和0交换(开头已经确定),0和非0交换(开头未确定变已确定)
swap(tmp2,s[1][y]);
cnt[0][x][c]++;cnt[1][y][c]++;
dfs(x,y+1);
cnt[1][y][c]--;cnt[0][x][c]--;//失败,回溯(回溯尽量去swap,这样更容易恢复状态)
swap(tmp,s[0][x]);//交换回来
swap(tmp2,s[1][y]);
}
}
}
}
int main(){
cin>>n;
for(int i=0;i<2;i++)cin>>s[i];
dfs(0,0);
cout<<"No\n";
}
lnc的工资
326E
题意:Inc的工资:给出n面的骰子,i对应a[i]元。问最终获得钱的期望是多少(结果对998244353取模)
规则如下:起初x=0,掷出y(>x)则给出a[y]元,同时x变成y,重复操作,直到y(<=x)时结束游戏
思路:
我们先算出现i的概率:
对于第一次:必然是1/n;
第二次:只能从1~i-1过来,所以是(i-1)/n*(1/n),化简成(i-1)*1/n^2
第三次:前两次都恰好从1~i-1中选了两个数,所以是C(2,i-1)*1/n^3 依次类推

然后所有概率相加:∑(i-1,k=0) (1/n)*C(k,i-1)*(1/n)^k
根据二项式定理转成∑(i-1,k=0) ((n+1)/n)^(i-1)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD=998244353;
ll qpow(ll a,ll b){
ll res=1;a%=MOD;
while(b){
if(b&1)res=(res*a)%MOD;
a=(a*a)%MOD;
b>>=1;
}
return res%MOD;
}
ll niyuan(ll x){
return qpow(x,MOD-2);
}
int main(){
int n;cin>>n;
ll nn=niyuan(n);//nn为n的逆元,相当于1/n
ll now=nn;//now即为当前的概率,最开始now就是i=1的概率
ll ans=0;
for(int i=1;i<=n;i++){
int x;cin>>x;//输入每个a[i]
ans=(ans+now*x)%MOD;//累加每个a[i]的期望
now=now*(n+1)%MOD*nn%MOD;//求下一个a[i]的概率,只需要多乘一次(n+1)/n,也就是(n+1)*nn即可
}
cout<<ans<<'\n';
}