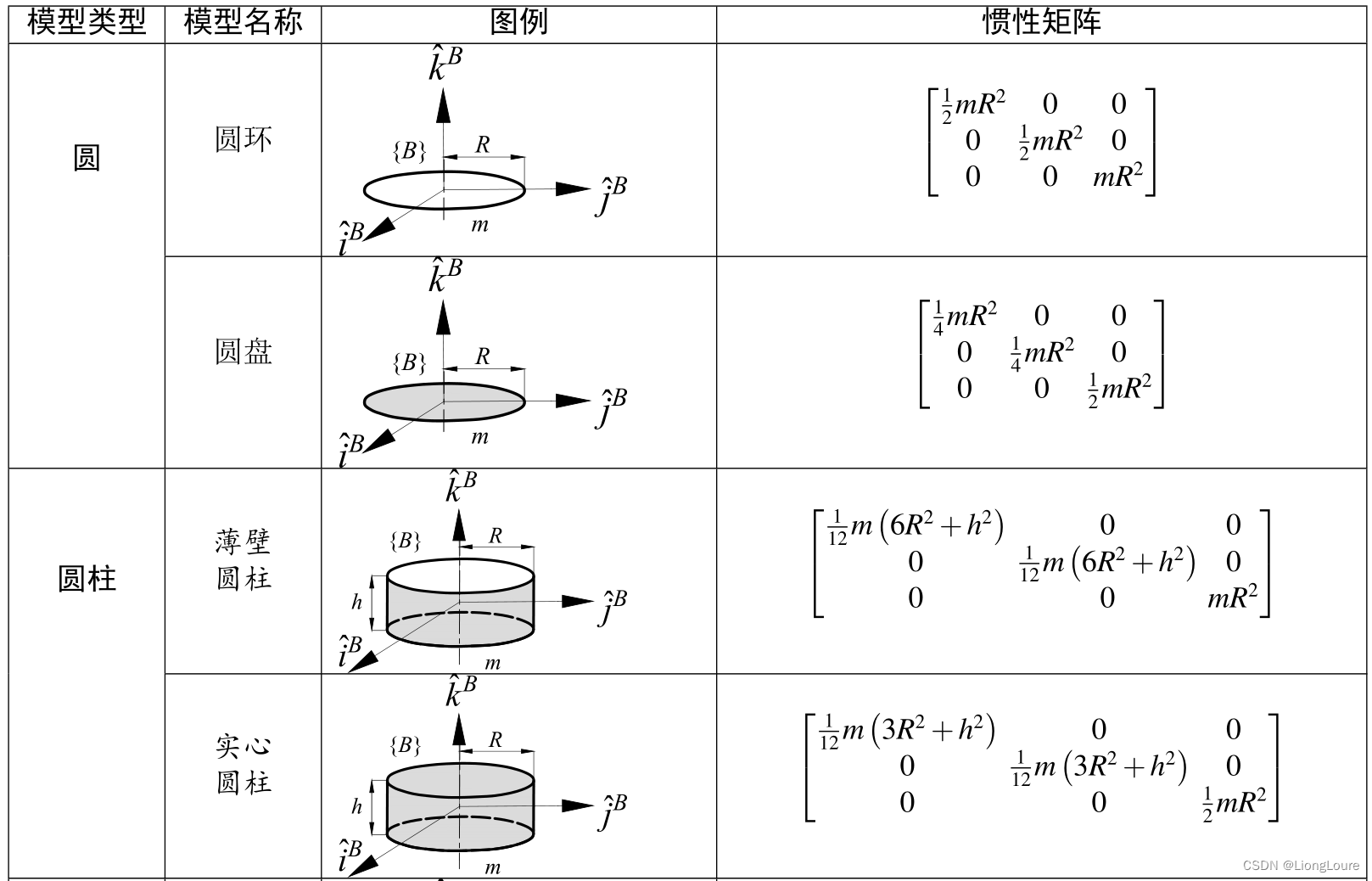
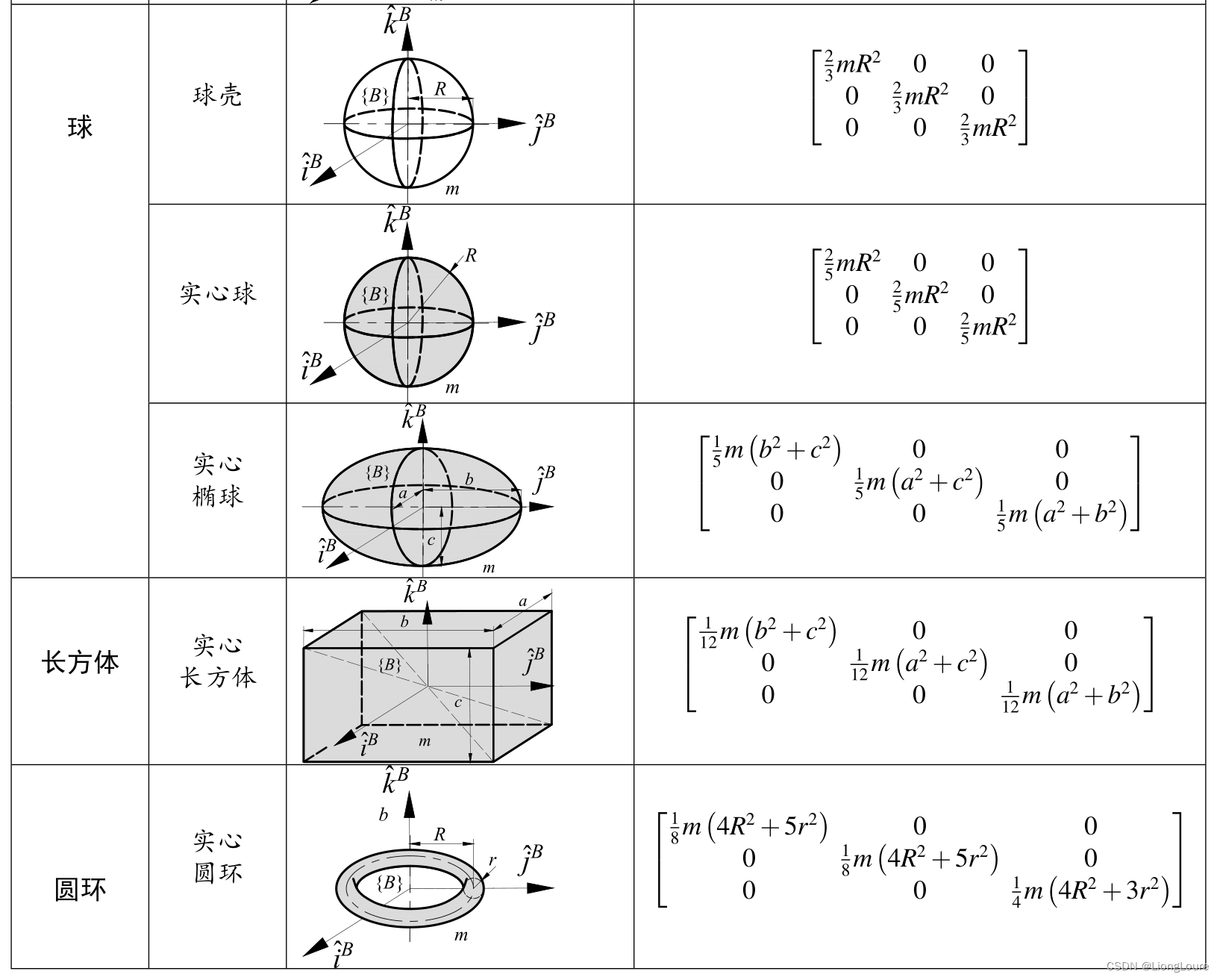
本文仅供学习使用，总结很多本现有讲述运动学或动力学书籍后的总结，从矢量的角度进行分析，方法比较传统，但更易理解，并且现有的看似抽象方法，两者本质上并无不同。

2024年底本人学位论文发表后方可摘抄
若有帮助请引用
本文参考：
黎 旭,陈 强 洪,甄 文 强 等.惯 性 张 量 平 移 和 旋 转 复 合 变 换 的 一 般 形 式 及 其 应 用[J].工 程 数 学 学 报,2022,39(06):1005-1011.

食用方法
质量点的动量与角动量
刚体的动量与角动量——力与力矩的关系
惯性矩阵的表达与推导——在刚体运动过程中的作用
惯性矩阵在不同坐标系下的表达
务必自己推导全部公式，并理解每个符号的含义

---

对${\vec{H}}_{{\Sigma }_{\mathrm{M}}/\mathrm{O}}^F$进一步处理可得：${\vec{H}}_{{\Sigma }_{\mathrm{M}}/\mathrm{O}}^F={\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot {\vec{R}}_{{\mathrm{OP}}_{\mathrm{i}}}^F\times \left({\vec{\omega }}^F\times {\vec{R}}_{{\mathrm{OP}}_{\mathrm{i}}}^F\right)={\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot {\vec{R}}_{{\mathrm{OP}}_{\mathrm{i}}}^F\times \left(-{\vec{R}}_{{\mathrm{OP}}_{\mathrm{i}}}^F\times {\vec{\omega }}^F\right)={\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot {\widetilde{\stackrel{⃗}{R}}}_{{\mathrm{OP}}_{\mathrm{i}}}^F\left(-{\widetilde{\stackrel{⃗}{R}}}_{{\mathrm{OP}}_{\mathrm{i}}}^F\right){\vec{\omega }}^F$。进而得出：$\Rightarrow \left[I\right]={\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot {\widetilde{\stackrel{⃗}{R}}}_{{\mathrm{OP}}_{\mathrm{i}}}^F\left(-{\widetilde{\stackrel{⃗}{R}}}_{{\mathrm{OP}}_{\mathrm{i}}}^F\right)$

2.2.4 牛顿-欧拉方程 Netwon-Euler equation

刚体动力学中常用：
$$\{\begin{array}{l}{\vec{F}}_{{\Sigma }_{\mathrm{M}}}^F=m_{\mathrm{total}}\cdot {\vec{a}}_{\mathrm{G}}^F\\ {\vec{M}}_{{\Sigma }_{\mathrm{M}}/\mathrm{G}}^F={\left[I\right]}_{{\Sigma }_{\mathrm{M}}/\mathrm{G}}^F{\vec{\alpha }}_{\mathrm{M}}^F+{\vec{\omega }}_{\mathrm{M}}^F\times \left({\left[I\right]}_{{\Sigma }_{\mathrm{M}}/\mathrm{G}}^F\cdot {\vec{\omega }}_{\mathrm{M}}^F\right)\end{array}$$

2.3 惯性矩阵的转换 Inertia-Matrix Transformation

对于空间中的运动刚体而言，刚体的惯性矩阵一般会根据运动坐标系 { M }    \left\{ M \right\} \,\, {M}的基矢量为基底进行计算，而不会直接考虑运动刚体在固定坐标系 { F }    \left\{ F \right\} \,\, {F}下的惯性矩阵。此时运动坐标系 { M }    \left\{ M \right\} \,\, {M}下计算得出的惯性矩阵记为：${\left[I\right]}^M$。若运动坐标系 { M }    \left\{ M \right\} \,\, {M}与固定坐标系 { F }    \left\{ F \right\} \,\, {F}的基矢量满足：$\left[\begin{array}{c}{\vec{i}}^M\\ {\vec{j}}^M\\ {\vec{k}}^M\end{array}\right]={\left[Q_{\mathrm{M}}^F\right]}^{\mathrm{T}}\left[\begin{array}{c}\hat{I}\\ \hat{J}\\ \hat{K}\end{array}\right]$，其中${\left[Q_{\mathrm{M}}^F\right]}^{\mathrm{T}}$为转换矩阵Transition Matrix，为正交矩阵Orthogonal Matrix（满足${\left[Q_{\mathrm{M}}^F\right]}^T={\left[Q_{\mathrm{M}}^F\right]}^{-1}=\left[Q_{\mathrm{F}}^M\right]$），$\left[Q_{\mathrm{M}}^F\right]$又称旋转矩阵Rotation~Matrix
（一个向量乘以一个正交阵，相当于对这个向量进行旋转）。也揭示了该矩阵的两个作用：基底转换（转换矩阵${\left[Q_{\mathrm{M}}^F\right]}^{\mathrm{T}}$）与向量旋转（旋转矩阵$\left[Q_{\mathrm{M}}^F\right]$），则考虑最开始的图有：

$${\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^F={\vec{R}}_{\mathrm{M}}^F+\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M$$

进而分析惯性矩阵，若 $O$ 点与固定坐标系原点 $F$ 重合，则有：
$$\begin{array}{rl}{\left[I\right]}_{{\Sigma }_{\mathrm{M}}}^F& =\sum _i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left[{\left({\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^F\right)}^T{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^F\cdot E-{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^F{\left({\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^F\right)}^T\right]\\ & =\sum _i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left[{\left({\vec{R}}_{\mathrm{M}}^F+\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^{\mathrm{T}}\left({\vec{R}}_{\mathrm{M}}^F+\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)\cdot E-\left({\vec{R}}_{\mathrm{M}}^F+\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right){\left({\vec{R}}_{\mathrm{M}}^F+\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^{\mathrm{T}}\right]\\ & =\{\begin{array}{c}\begin{array}{c}\underbrace{m_{\mathrm{total}}\cdot \left[{\left({\vec{R}}_{\mathrm{M}}^F\right)}^{\mathrm{T}}{\vec{R}}_{\mathrm{M}}^F\cdot E-{\vec{R}}_{\mathrm{M}}^F{\left({\vec{R}}_{\mathrm{M}}^F\right)}^{\mathrm{T}}\right]}\\ {\left[I_1\right]}_{{\Sigma }_{\mathrm{M}}}^F\end{array}+\\ \begin{array}{c}\underbrace{\left[Q_{\mathrm{M}}^F\right]\left(\sum _i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left[{\left({\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^{\mathrm{T}}{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\cdot E-{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M{\left({\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^{\mathrm{T}}\right]\right){\left[Q_{\mathrm{M}}^F\right]}^{\mathrm{T}}+}\\ {\left[I_2\right]}_{{\Sigma }_{\mathrm{M}}}^F\end{array}\\ \begin{array}{c}\underbrace{m_{\mathrm{total}}\cdot \left[{\left({\vec{R}}_{\mathrm{M}}^F\right)}^{\mathrm{T}}\left(\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{\mathrm{CoM}}^M\right)\cdot E-{\vec{R}}_{\mathrm{M}}^F{\left(\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{\mathrm{CoM}}^M\right)}^{\mathrm{T}}\right]}\\ {\left[I_3\right]}_{{\Sigma }_{\mathrm{M}}}^F\end{array}+\\ \begin{array}{c}\underbrace{m_{\mathrm{total}}\cdot \left[{\left(\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{\mathrm{CoM}}^M\right)}^T{\vec{R}}_{\mathrm{M}}^F\cdot E-\left(\left[Q_{\mathrm{M}}^F\right]{\vec{R}}_{\mathrm{CoM}}^M\right){\left({\vec{R}}_{\mathrm{M}}^F\right)}^{\mathrm{T}}\right]}\\ {\left[I_4\right]}_{{\Sigma }_{\mathrm{M}}}^F\end{array}\end{array}\\ & ={\left[I_1\right]}_{{\Sigma }_{\mathrm{M}}}^F+{\left[I_2\right]}_{{\Sigma }_{\mathrm{M}}}^F+{\left[I_3\right]}_{{\Sigma }_{\mathrm{M}}}^F+{\left[I_4\right]}_{{\Sigma }_{\mathrm{M}}}^F\end{array}$$

其中，${\left[I_2\right]}_{{\Sigma }_{\mathrm{M}}}^F=\left[Q_{\mathrm{M}}^F\right]\left({\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left[{\left({\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^{\mathrm{T}}{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\cdot E-{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M{\left({\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^{\mathrm{T}}\right]\right){\left[Q_{\mathrm{M}}^F\right]}^{\mathrm{T}}=\left[Q_{\mathrm{M}}^F\right]{\left[I\right]}_{{\Sigma }_{\mathrm{M}}}^M{\left[Q_{\mathrm{M}}^F\right]}^{\mathrm{T}}$，对上式进行讨论：

• 纯回转： 当${\vec{R}}_{\mathrm{M}}^F=0$时，化简为：
  $${{\left[I\right]}_{{\Sigma }_{\mathrm{M}}}^F|}_{{\vec{\mathrm{R}}}_{\mathrm{M}}^F=0}={\left[I_2\right]}_{{\Sigma }_{\mathrm{M}}}^F=\left[Q_{\mathrm{M}}^F\right]\left(\sum _i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left[{\left({\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^{\mathrm{T}}{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\cdot E-{\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M{\left({\vec{R}}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^{\mathrm{T}}\right]\right){\left[Q_{\mathrm{M}}^F\right]}^{\mathrm{T}}=\left[Q_{\mathrm{M}}^F\right]{\left[I\right]}_{{\Sigma }_{\mathrm{M}}}^M{\left[Q_{\mathrm{M}}^F\right]}^{\mathrm{T}}$$
• 纯移动： 当${\vec{R}}_{\mathrm{M}}^F\ne 0$且$\left[Q_{\mathrm{M}}^F\right]=E$时，化简为：
  $${{\left[I\right]}_{{\Sigma }_{\mathrm{M}}}^F|}_{{\vec{\mathrm{R}}}_{\mathrm{M}}^F\ne 0,\left[Q_{\mathrm{M}}^F\right]=\mathrm{E}}={\left[I_1\right]}_{{\Sigma }_{\mathrm{M}}}^F+{\left[I\right]}_{{\Sigma }_{\mathrm{M}}}^M$$
  上式也称为惯性矩阵的平行轴定理Parallel Axis Theorem。
• 运动坐标系原点与质心点重合： 当${\vec{R}}_{\mathrm{CoM}}^F=0$时，化简为：
  $${{\left[I\right]}^F|}_{{\vec{R}}_{\mathrm{CoM}}^F=0}=\left[I_1\right]+\left[I_2\right]$$

2.4 惯性矩阵的主轴定理} Principal Axis Theorem

进一步观察惯性矩阵：
${\left[I\right]}^M=\left[\begin{array}{ccc}{\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left[{\left(y_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^2+{\left(z_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^2\right]& -{\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot x_{{\mathrm{P}}_{\mathrm{i}}}^M{y}_{{\mathrm{P}}_{\mathrm{i}}}^M& -{\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left(x_{{\mathrm{P}}_{\mathrm{i}}}^M{z}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)\\ -{\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left(y_{{\mathrm{P}}_{\mathrm{i}}}^M{x}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)& {\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left[{\left(x_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^2+{\left(z_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^2\right]& -{\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left(y_{{\mathrm{P}}_{\mathrm{i}}}^M{z}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)\\ -{\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left(z_{{\mathrm{P}}_{\mathrm{i}}}^M{x}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)& -{\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left(z_{{\mathrm{P}}_{\mathrm{i}}}^M{y}_{{\mathrm{P}}_{\mathrm{i}}}^M\right)& {\sum }_i^N{m}_{{\mathrm{P}}_{\mathrm{i}}}\cdot \left[{\left(x_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^2+{\left(y_{{\mathrm{P}}_{\mathrm{i}}}^M\right)}^2\right]\end{array}\right]$，为对称矩阵Symmetric Matrix（此时默认 $M$ 点与 $F$ 点重合），则一定能够对角化。

等价于找到另一原点与 $M$ 重合的坐标系 $B$ ，使得：${\left[I\right]}^B=\left[\begin{array}{ccc}{I}_{\mathrm{xx}}^B& 0& 0\\ 0& I_{\mathrm{yy}}^B& 0\\ 0& 0& I_{\mathrm{zz}}^B\end{array}\right]$，根据矩阵对角化Matrix Diagonalizing的原理，结合纯回转推导可得：
$${\left[I\right]}^M=\left[Q_{\mathrm{B}}^M\right]{\left[I\right]}^B{\left[Q_{\mathrm{B}}^M\right]}^{\mathrm{T}}$$

其中：

• $\left[Q_{\mathrm{B}}^M\right]$ 满足 $\left[\begin{array}{c}{\vec{i}}^B\\ {\vec{j}}^B\\ {\vec{k}}^B\end{array}\right]={\left[Q_{\mathrm{B}}^M\right]}^{\mathrm{T}}\left[\begin{array}{c}{\vec{i}}^M\\ {\vec{j}}^M\\ {\vec{k}}^M\end{array}\right]$；
• $\left(I_{\mathrm{xx}}^B,I_{\mathrm{yy}}^B,I_{\mathrm{zz}}^B\right)$ 为矩阵 ${\left[I\right]}^M$的特征值Eigenvalue；
• $\left[Q_{\mathrm{B}}^M\right]$ 为对应于特征值矩阵 ${\left[I\right]}^B$的特征基Standard Eigenvalue Basis(列向量)；