题目链接

[NOIP2012 提高组] 开车旅行

题目描述

小 $\text{A}$ 和小 $\text{B}$ 决定利用假期外出旅行，他们将想去的城市从 $1$ 到 $n$ 编号，且编号较小的城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 $i$ 的海拔高度为$h_i$，城市 $i$ 和城市 $j$ 之间的距离 $d_{i,j}$ 恰好是这两个城市海拔高度之差的绝对值，即 $d_{i,j}=|h_i-h_j|$。

旅行过程中，小 $\text{A}$ 和小 $\text{B}$ 轮流开车，第一天小 $\text{A}$ 开车，之后每天轮换一次。他们计划选择一个城市 $s$ 作为起点，一直向东行驶，并且最多行驶 $x$ 公里就结束旅行。

小 $\text{A}$ 和小 $\text{B}$ 的驾驶风格不同，小 $\text{B}$ 总是沿着前进方向选择一个最近的城市作为目的地，而小 $\text{A}$ 总是沿着前进方向选择第二近的城市作为目的地（注意：本题中如果当前城市到两个城市的距离相同，则认为离海拔低的那个城市更近）。如果其中任何一人无法按照自己的原则选择目的城市，或者到达目的地会使行驶的总距离超出 $x$ 公里，他们就会结束旅行。

在启程之前，小 $\text{A}$ 想知道两个问题：

1、 对于一个给定的 $x=x_0$，从哪一个城市出发，小 $\text{A}$ 开车行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值最小（如果小 $\text{B}$ 的行驶路程为 $0$，此时的比值可视为无穷大，且两个无穷大视为相等）。如果从多个城市出发，小 $\text{A}$ 开车行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值都最小，则输出海拔最高的那个城市。

2、对任意给定的 $x=x_i$ 和出发城市 $s_i$，小 $\text{A}$ 开车行驶的路程总数以及小 $\text{B}$ 行驶的路程总数。

输入格式

第一行包含一个整数 $n$，表示城市的数目。

第二行有 $n$ 个整数，每两个整数之间用一个空格隔开，依次表示城市 $1$ 到城市 $n$ 的海拔高度，即 $h_1,h_2...h_n$，且每个 $h_i$ 都是互不相同的。

第三行包含一个整数 $x_0$。

第四行为一个整数 $m$，表示给定 $m$ 组 $s_i$ 和 $x_i$。

接下来的 $m$ 行，每行包含 $2$ 个整数 $s_i$ 和 $x_i$，表示从城市$s_i$ 出发，最多行驶 $x_i$ 公里。

输出格式

输出共 $m+1$ 行。

第一行包含一个整数 $s_0$，表示对于给定的 $x_0$，从编号为 $s_0$ 的城市出发，小 $\text{A}$ 开车行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值最小。

接下来的 $m$ 行，每行包含 $2$ 个整数，之间用一个空格隔开，依次表示在给定的 $s_i$ 和 $x_i$ 下小 $\text{A}$ 行驶的里程总数和小 $\text{B}$ 行驶的里程总数。

样例 #1

样例输入 #1

4 
2 3 1 4 
3 
4 
1 3 
2 3 
3 3 
4 3

样例输出 #1

1 
1 1 
2 0 
0 0 
0 0

样例 #2

样例输入 #2

10 
4 5 6 1 2 3 7 8 9 10 
7 
10 
1 7 
2 7 
3 7 
4 7 
5 7 
6 7 
7 7 
8 7 
9 7 
10 7

样例输出 #2

2 
3 2 
2 4 
2 1 
2 4 
5 1 
5 1 
2 1 
2 0 
0 0 
0 0

提示

【样例1说明】

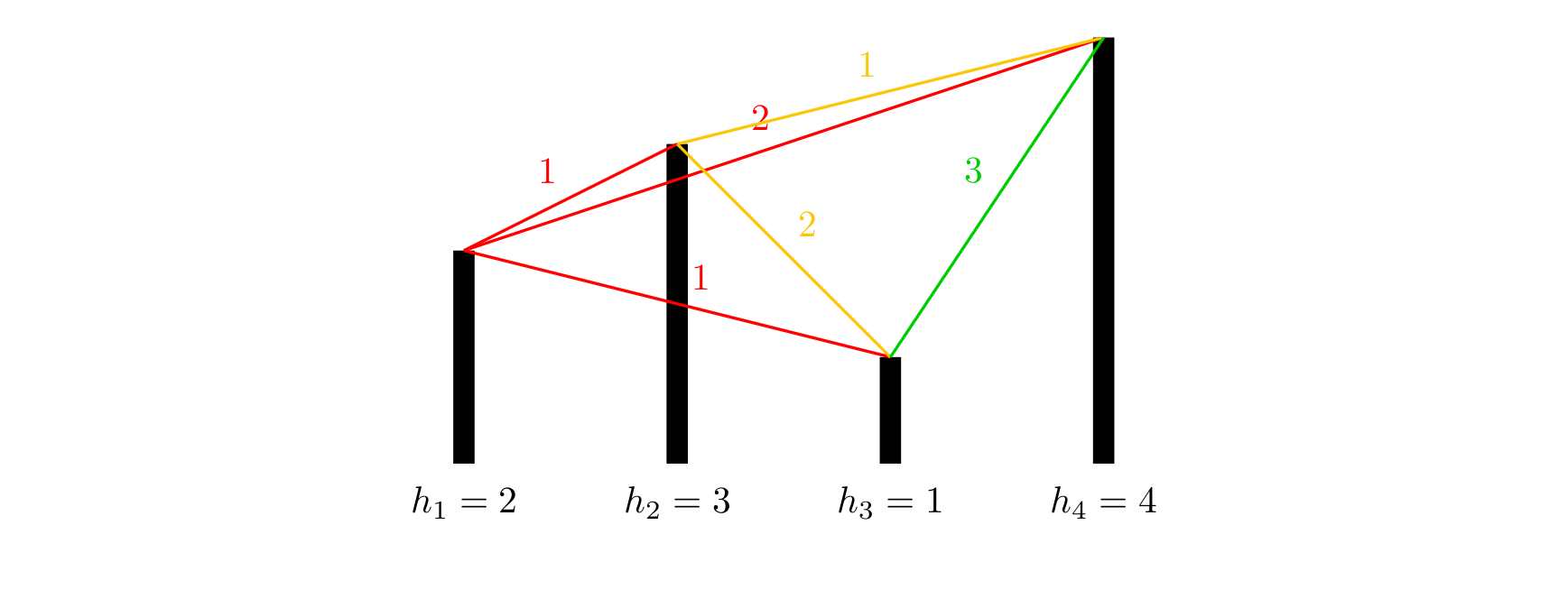
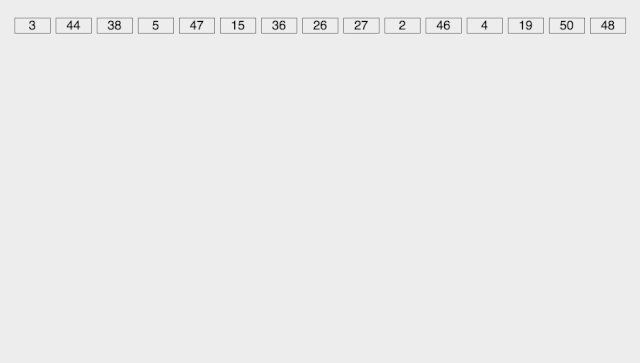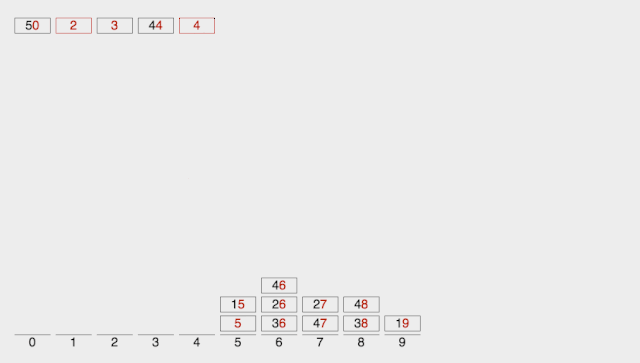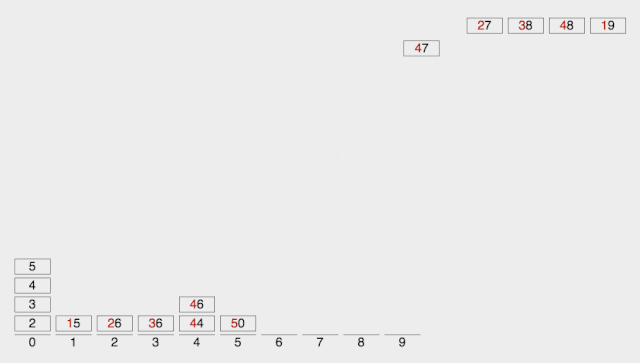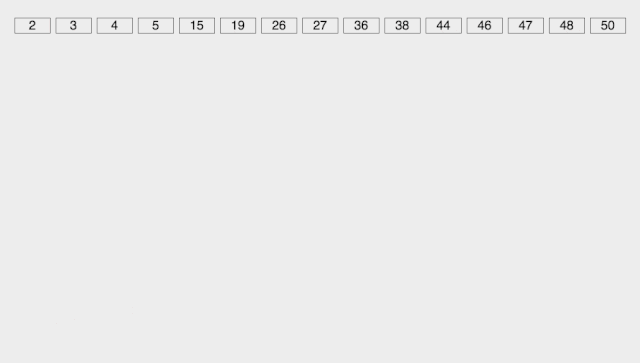
各个城市的海拔高度以及两个城市间的距离如上图所示。

如果从城市 $1$ 出发，可以到达的城市为 $2,3,4$，这几个城市与城市 $1$ 的距离分别为 $1,1,2$，但是由于城市 $3$ 的海拔高度低于城市 $2$，所以我们认为城市 $3$ 离城市 $1$ 最近，城市 $2$ 离城市 $1$ 第二近，所以小A会走到城市 $2$。到达城市 $2$ 后，前面可以到达的城市为 $3,4$，这两个城市与城市 $2$ 的距离分别为 $2,1$，所以城市 $4$ 离城市 $2$ 最近，因此小B会走到城市$4$。到达城市 $4$ 后，前面已没有可到达的城市，所以旅行结束。

如果从城市 $2$ 出发，可以到达的城市为 $3,4$，这两个城市与城市 $2$ 的距离分别为 $2,1$，由于城市 $3$ 离城市 $2$ 第二近，所以小 $\text{A}$ 会走到城市 $3$。到达城市 $3$ 后，前面尚未旅行的城市为 $4$，所以城市 $4$ 离城市 $3$ 最近，但是如果要到达城市 $4$，则总路程为 $2+3=5>3$，所以小 $\text{B}$ 会直接在城市 $3$ 结束旅行。

如果从城市 $3$ 出发，可以到达的城市为 $4$，由于没有离城市 $3$ 第二近的城市，因此旅行还未开始就结束了。

如果从城市 $4$ 出发，没有可以到达的城市，因此旅行还未开始就结束了。

【样例2说明】

当 $x=7$ 时，如果从城市 $1$ 出发，则路线为 $1\to 2\to 3\to 8\to 9$，小 $\text{A}$ 走的距离为 $1+2=3$，小 $\text{B}$ 走的距离为 $1+1=2$。（在城市 $1$ 时，距离小 $\text{A}$ 最近的城市是 $2$ 和 $6$，但是城市 $2$ 的海拔更高，视为与城市 $1$ 第二近的城市，所以小 $\text{A}$ 最终选择城市 $2$；走到$9$ 后，小 $\text{A}$ 只有城市 $10$ 可以走，没有第二选择可以选，所以没法做出选择，结束旅行）

如果从城市 $2$ 出发，则路线为 $2\to 6\to 7$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为 $2,4$。

如果从城市 $3$ 出发，则路线为 $3\to 8\to 9$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$2,1$。

如果从城市 $4$ 出发，则路线为 $4\to 6\to 7$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为 $2,4$。

如果从城市 $5$ 出发，则路线为 $5\to 7\to 8$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为 $5,1$。

如果从城市 $6$ 出发，则路线为 $6\to 8\to 9$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$5,1$。

如果从城市 $7$ 出发，则路线为 $7\to 9\to 10$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$2,1$。

如果从城市 $8$ 出发，则路线为 $8\to 10$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$2,0$。

如果从城市 $9$ 出发，则路线为 $9$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为 $0,0$（旅行一开始就结束了）。

如果从城市 $10$ 出发，则路线为 $10$，小 $\text{A}$ 和小 $\text{B}$ 走的距离分别为$0,0$。

从城市 $2$ 或者城市 $4$ 出发小 $\text{A}$ 行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值都最小，但是城市 $2$ 的海拔更高，所以输出第一行为 $2$。

【数据范围与约定】

对于 $30\%$ 的数据，有$1\le n\le 20,1\le m\le 20$；
对于$40\%$ 的数据，有$1\le n\le 100,1\le m\le 100$；
对于 $50\%$ 的数据，有$1\le n\le 100,1\le m\le 1000$；
对于 $70\%$ 的数据，有$1\le n\le 1000,1\le m\le 10^4$；
对于 $100\%$ 的数据：$1\le n,m\le 10^5$，$-10^9\le h_i\le 10^9$，$1\le s_i\le n$，$0\le x_i\le 10^9$
数据保证 $h_i$ 互不相同。

算法思想

根据题目描述，本题要求的是选择一个城市 $s$ 作为起点，一直向东行驶，并且最多行驶 $x$ 公里就结束旅行时，小 $\text{A}$ 开车行驶的路程总数以及小 $\text{B}$ 行驶的路程总数。

由于小$\text{A}$和小$\text{B}$一直向东行驶，并且最多行驶 $x$ 公里就结束旅行，可以使用倍增法统计出小 $\text{A}$ 和小 $\text{B}$ 开车行驶的路程总数$la$和$lb$。

状态表示

• $da(0,s,i)$表示从城市$s$出发，小$\text{A}$先走，两人轮流行驶了$2^i$次，小$\text{A}$行驶的总距离。
• $da(1,s,i)$表示从城市$s$出发，小$\text{B}$先走，两人轮流行驶了$2^i$次，小$\text{A}$行驶的总距离。
• $db(0,s,i)$表示从城市$s$出发，小$\text{A}$先走，两人轮流行驶了$2^i$次，小$\text{B}$行驶的总距离。
• $db(1,s,i)$表示从城市$s$出发，小$\text{B}$先走，两人轮流行驶了$2^i$次，小$\text{B}$行驶的总距离。

有了上述状态，如何求从 $s$ 出发，最多行驶 $x$ 公里时的$la$和$lb$呢？不妨设两人轮流行驶了$k$次，以二进制的方式分析，假设$k=(011010010{)}_2$，那么
$$\begin{gathered} la=da(0,s,7)+da(0,s_1,6)+da(0,s_2,4)+da(0,s_3,1) \\ lb=db(0,s,7)+db(0,s_1,6)+db(0,s_2,4)+db(0,s_3,1) \end{gathered}$$

其中$s_1,s_2,s_3...$为中间经过的城市。要求解中间经过的城市，还需要预处理

• $f(0,s,i)$表示从城市$s$出发，小$\text{A}$先走，两人轮流行驶了$2^i$次到达的城市编号
• $f(1,s,i)$表示从城市$s$出发，小$\text{B}$先走，两人轮流行驶了$2^i$次到达的城市编号

由于题目要求，小$\text{A}$和小$\text{B}$的驾驶风格不同。因此，还需要预处理出：

• $ga(i)$表示小$\text{A}$从城市$s$出发能够到达的城市编号
• $gb(i)$表示小$\text{B}$从城市$s$出发能够到达的城市编号

下面再来考虑一些如何计算上述状态

状态计算

1、 先来看一下如何计算$ga$和$gb$：

• 由于小$\text{A}$总是沿着前进方向选择第二近的城市作为目的地，那么就是求城市$s$右边和它的海拔高度之差第$2$小的城市
• 小$\text{B}$ 总是沿着前进方向选择一个最近的城市作为目的地，那么就是求城市$s$右边和它的海拔高度之差最小的城市

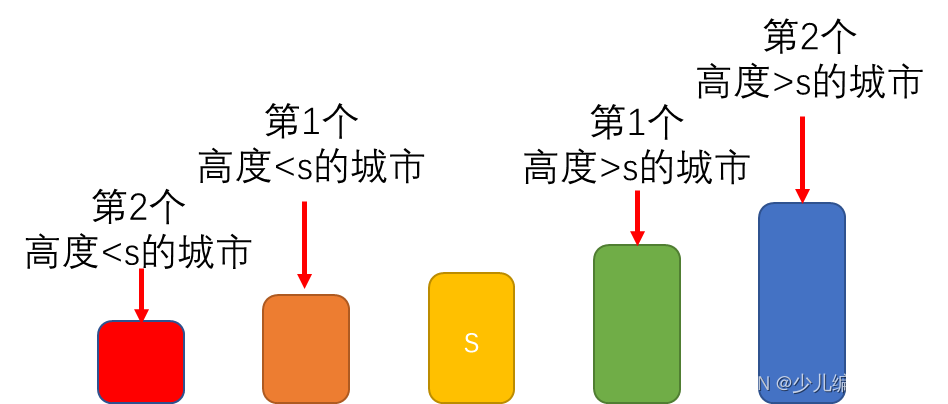
即在$s$右侧的城市中，查找与$s$高度之差的绝对值最小的两个城市，其原理类似于博主的这篇文章——邻值查找。

为了快速查找目标，可以使用set作为容器，从后向前遍历每个城市：

• 查找第$1$个高度大于$h[s]$的城市和第$2$个高度大于$h[s]$的城市
• 查找第$1$个高度小于$h[s]$的城市和第$2$个高度小于$h[s]$的城市
• 那么，目标就在这$4$个城市之间，如下图所示。
• 再将城市$s$插入到set中。
  

2、再看如何计算$f(0,s,i)$和$f(0,s,i)$

• 当$i=0$时，表示从$s$出发行驶$1$次，那么$f(0,s,0)=ga(s)$，$f(1,s,0)=gb(s)$，
• 当$i=1$时，表示从$s$出发行驶$2$次
  • 第$1$次小$\text{A}$先驾驶从$s$行驶到$f(0,s,0)$
  • 第$2$次换小$\text{B}$驾驶从$f(0,s,0)$行驶到了$f(1,f(0,s,0),0)$
  • $k$表示由谁先驾驶，$k=0$表示小$\text{A}$先驾驶，$k=1$表示小$\text{B}$先驾驶，那么$f(k,s,1)=f(1-k,f(k,s,0),0)$
• 当$i>1$时，表示从$s$出发行驶$2^i$次，也可以分成两部分
  • 第一部分， 小$\text{A}$先驾驶从$s$行驶到$f(0,s,i-1)$
  • 第二部分，由于$i>1$，$2^{i-1}$是偶数，不换人，还有由小$\text{A}$先驾驶从$f(0,s,i-1)$，行驶到$f(0,f(0,s,i-1),i-1)$
  • 即$f(k,s,i)=f(k,f(k,s,i-1),i-1)$

3、最后再计算$da$和$db$

• 当$i=0$时，即行驶$1$次

  • $da(0,s,0)$表示小$\text{A}$先走，行驶$1$次，会从城市$s$到达$ga(s)$，那么$da(0,s,0)=dist(s,ga(s))$，即这两个城市海拔高度之差的绝对值；如果小$\text{B}$先走，那么小$\text{A}$行驶的距离为$0$，即$da(1,s,0)=0$
  • 同理，$db(1,s,0)=dist(s,gb(s))$，$db(0,s,0)=0$

• 当$i=1$时，即行驶$2$次，可以分成两部分，不妨用$k$表示谁先行驶， k = { 0 , 1 } k=\{0,1\} k={0,1}

  • 第一部分从$s$出发，行驶$1$次，走到$f(k,s,0)$，小$\text{A}$行驶的距离$da(k,s,0)$，
    小$\text{B}$行驶的距离为$db(k,s,0)$
  • 第二部分从$f(k,s,0)$出发，换人行驶$1$次，小$\text{A}$行驶的距离$da(1-k,f(k,s,0),0)$，
    小$\text{B}$行驶的距离为$db(k,f(k,s,0),0)$
  • 那么，$da(k,s,1)=da(k,s,0)+da(1-k,f(k,s,0),0)$，$db(k,s,1)=db(k,s,0)+db(1-k,f(k,s,0),0)$

• 当$i>1$时，即行驶$2^i$次，也可以分成两部分，$k$表示谁先行驶， k = { 0 , 1 } k=\{0,1\} k={0,1}

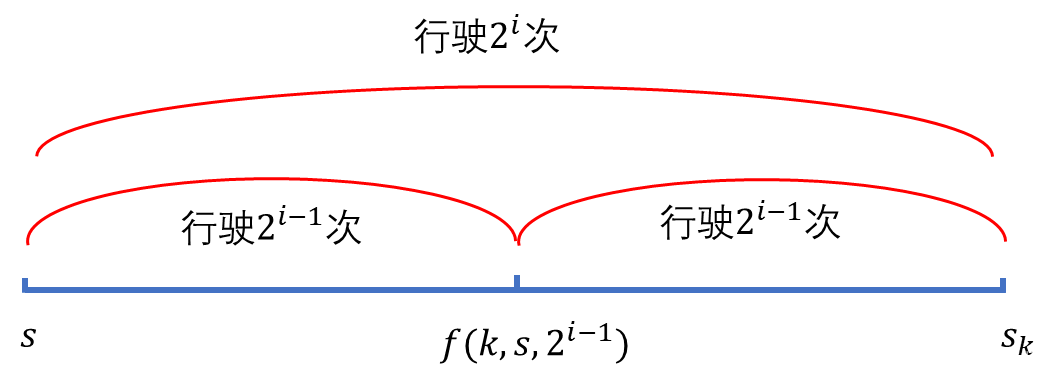
  • $da(k,s,i)=da(k,s,i-1)+da(k,f(k,s,i-1),i-1)$
  • $db(k,s,i)=db(k,s,i-1)+db(1-k,f(k,s,i-1),i-1)$

如下图所示

时间复杂度

• 预处理$ga,gb$需要从后向前遍历每个城市$s$，查找与$s$高度之差的绝对值最小的两个城市，使用set容器查找的时间复杂度为$O(logn)$，总的时间复杂度为$O(nlogn)$
• 通过倍增法预处理$f$的时间复杂度为$O(nlogn)$
• 通过倍增法预处理$da,db$的时间复杂度为$O(nlogn)$
• 第一问求对于给定的 $x$，从哪个城市出发，小 $\text{A}$ 开车行驶的路程总数与小 $\text{B}$ 行驶的路程总数的比值最小，需要枚举每个城市作为起点，求$la$和$lb$，时间复杂度为$O(nlogn)$
• 第二问一共有$m$个询问，求在给定的 $s$ 和 $x$ 情况下求小 $\text{A}$ 行驶的里程总数和小 $\text{B}$ 行驶的里程总数，时间复杂度为$O(mlogn)$

总的时间复杂度为$O(nlogn)=10^5\times 17$

代码实现

#include <iostream>
#include <set>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;
const int N = 1e5 + 10, M = 17;
const LL INF = 1e18; 
int n, h[N];
int ga[N], gb[N]; //ga[i]表示小A从i出发能到达的城市
int f[2][N][M]; //f[0][s][i]表示从s出发，小A先走，轮流行驶2^i时到达的城市编号
int da[2][N][M], db[2][N][M];
void init_g()
{
    set<PLI> S;
    //防止查找越界，插入4个边界
    S.insert({-INF, 0}), S.insert({-INF + 1, 0});
    S.insert({INF, 0}), S.insert({INF + 1, 0});
    PLI b[4]; //被选城市
    //从后向前遍历城市，查找右侧第一个大于h[i]的位置
    for(int i = n; i >= 0; i --)
    {
        PLI t(h[i], i);
        auto it = S.upper_bound(t);
        it ++; //移动到右侧第二个大于h[i]的位置
        for(int k = 0; k < 4; k ++) b[k] = *it --;
        //从备选的4个备选城市中查找差值第1小和第2小的城市
        LL d1 = INF, d2 = INF;
        int p1, p2;
        for(int k = 3; k >= 0; k --)
        {
            LL d = abs(h[i] - b[k].first);
            if(d < d1) {
                d2 = d1, d1 = d;
                p2 = p1, p1 = b[k].second; 
            }
            else if(d < d2) {
                d2 = d, p2 = b[k].second;
            }
        }
        //小A选择第二近的城市作为目的地，小B选择一个最近的城市作为目的地，
        ga[i] = p2, gb[i] = p1;
        S.insert(t);
    }
}
void init_f()
{
    //初始状态，从每个城市出发行驶1次能到达的城市
    for(int s = 1; s <= n; s ++) 
    {
        f[0][s][0] = ga[s], f[1][s][0] = gb[s];
    }
    //状态计算
    for(int i = 1; i < M; i ++)
        for(int s = 1; s <= n; s ++)
            for(int k = 0; k < 2; k ++)
            {
                if(i == 1) //行驶2次
                    f[k][s][i] = f[1 - k][f[k][s][0]][0];
                else //行驶2^i
                    f[k][s][i] = f[k][f[k][s][i - 1]][i - 1];
            }
}
//获取两个城市之间的距离
int get_dis(int a, int b)
{
    return abs(h[a] - h[b]);
}
void init_d()
{
    //初始状态，计算从每个城市出发行驶1次能够走的额距离
    for(int s = 1; s <= n; s ++)
    {
        da[0][s][0] = get_dis(s, ga[s]);
        db[1][s][0] = get_dis(s, gb[s]);
    }
    //状态计算
    for(int i = 1; i < M; i ++)
        for(int s = 1; s <= n; s ++)
            for(int k = 0; k < 2; k ++)
            {
                if(i == 1) //行驶2次
                {
                    da[k][s][i] = da[k][s][i - 1] + da[1 - k][f[k][s][i - 1]][i - 1];
                    db[k][s][i] = db[k][s][i - 1] + db[1 - k][f[k][s][i - 1]][i - 1];
                }
                else //行驶2^i次
                {
                    da[k][s][i] = da[k][s][i - 1] + da[k][f[k][s][i - 1]][i - 1];
                    db[k][s][i] = db[k][s][i - 1] + db[k][f[k][s][i - 1]][i - 1];
                }
            }
}
//计算从城市s出发，行驶总距离不超过s时，小A和小B各自走的总距离
void work(int s, int x, int &la, int &lb)
{
    la = lb = 0;
    //枚举行驶次数
    for(int i = M - 1; i >= 0; i --)
    {
        //如果能够到达城市，并且总距离不超过x
        if(f[0][s][i] && la + lb + da[0][s][i] + db[0][s][i] <= x)
        {
            la += da[0][s][i], lb += db[0][s][i];
            s = f[0][s][i];//行驶到新的城市s
        }
    }
}
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) scanf("%d", &h[i]);
    //预处理状态
    init_g();
    init_f();
    init_d();
    //第一问
    int x;
    scanf("%d", &x);
    int ans = 0, max_h = 0;
    double min_r = INF;
    for(int s = 1; s <= n; s ++)
    {
        int la, lb;
        work(s, x, la, lb);
        double r = lb == 0 ? INF : (double) la / lb;
        //取最小比值，比值相同取海拔更高的城市
        if(r < min_r || r == min_r && h[s] > max_h)
        {
            min_r = r, max_h = h[s], ans = s;
        }
    }
    printf("%d\n", ans);
    //第二问
    int m;
    scanf("%d", &m);
    while (m -- )
    {
        int s, x, la, lb;
        scanf("%d%d", &s, &x);
        work(s, x, la, lb);
        printf("%d %d\n", la, lb);
    }
    return 0;
}