day 43
代码随想录
2024.1.10
发烧中。。。简单过一遍等二刷DP问题！（最近赶一篇paper！）

1. 1049最后一块石头的重量

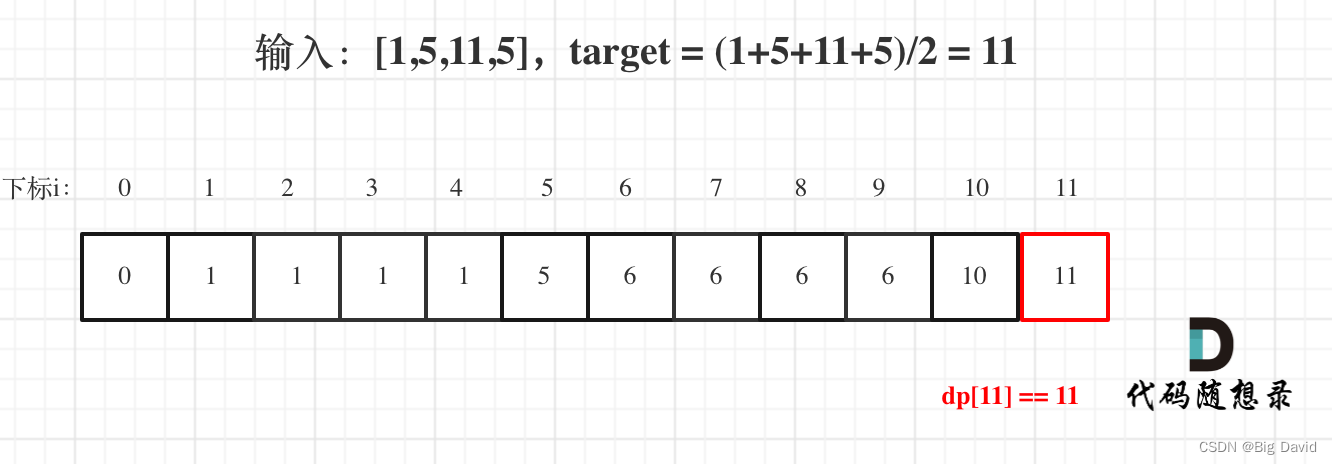
1. dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。
2. 与01背包一样，dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3. 因为重量都不会是负数，所以dp[j]都初始化为0就可以了，这样在递归公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);中dp[j]才不会初始值所覆盖。
4. 如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        vector<int> dp(15001,0);
        int sum=0;
        for(int i =0;i<stones.size();i++)  sum += stones[i];
        int target = sum/2;
        for(int i=0;i<stones.size();i++)
            for(int j=target;j>=stones[i];j--)
                dp[j] = max(dp[j], dp[j-stones[i]]+stones[i]);
        return sum-dp[target]-dp[target];
    }
};

2. 494目标和
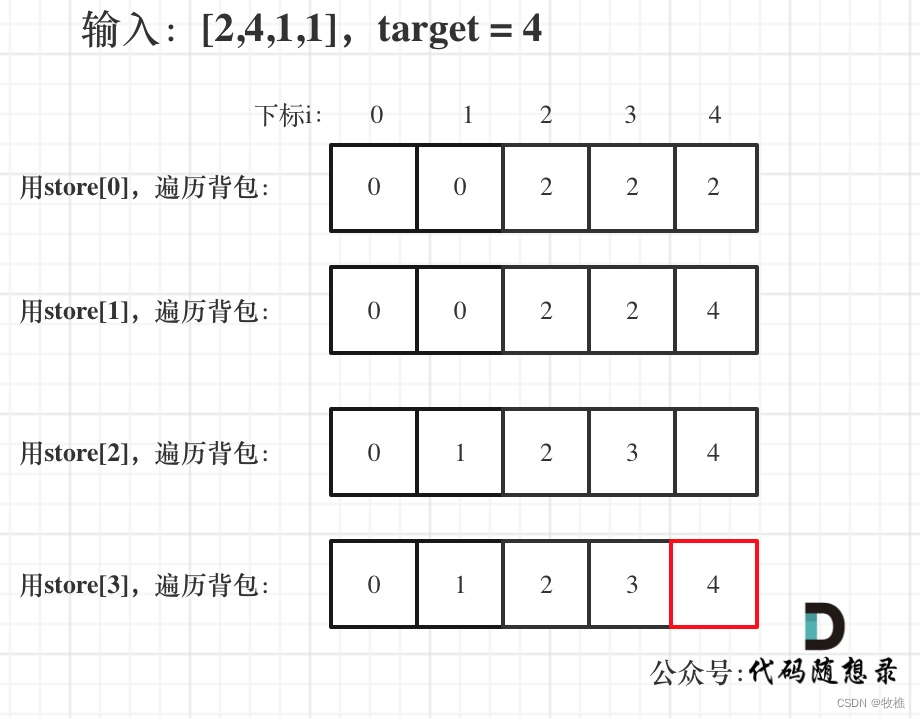
神奇的思路，也就是将数组分为两部分，差等于target，也就是找满足x=(sum+target)/2，一共有多少种x的组合方法，也就是背包问题了

1. dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

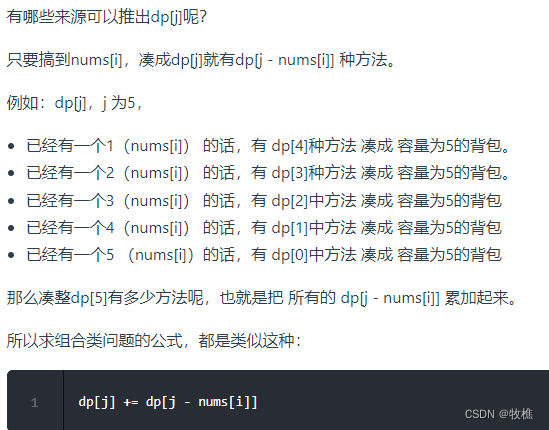
3. dp[0] 为 1
4. 01背包问题一维dp的遍历，nums放在外循环，target在内循环，且内循环倒序。

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) sum += nums[i];
        if (abs(target) > sum) return 0; // 此时没有方案
        if ((target + sum) % 2 == 1) return 0; // 此时没有方案
        int bagSize = (target + sum) / 2;
        vector<int> dp(bagSize + 1, 0);
        dp[0] = 1;
        for (int i = 0; i < nums.size(); i++) {
            for (int j = bagSize; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[bagSize];

    }
};

3. 474一和零
本题是一道01背包问题

1. dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

2. dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。

   dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

   然后我们在遍历的过程中，取dp[i][j]的最大值。

   所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

3. 初始化为0

4. 外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历！

5. 略!

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0
        for (string str : strs) { // 遍历物品
            int oneNum = 0, zeroNum = 0;
            for (char c : str) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};