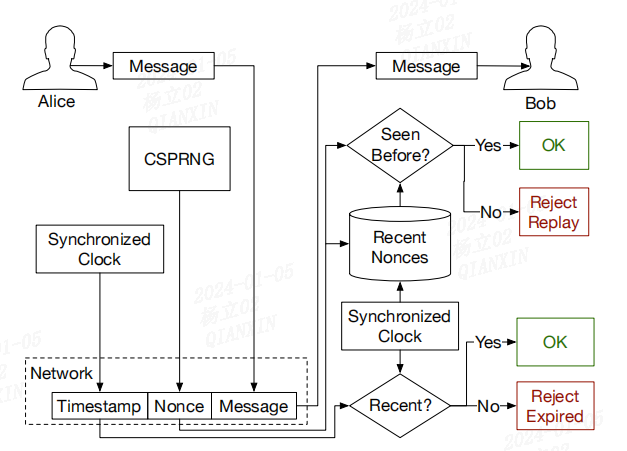
C2-4.3.1 多个决策树——随机森林
参考链接
1、为什么要使用多个决策树——随机森林?
- 决策树的缺点:
A small change in the data can cause a large change in the structure of the decision tree causing instability
即:对数据集 中微小的变化敏感,往往一棵树的结果不是那么理想—— 通过多个决策树的组合,让它对数据变化没那么敏感,得到更加准确的结果
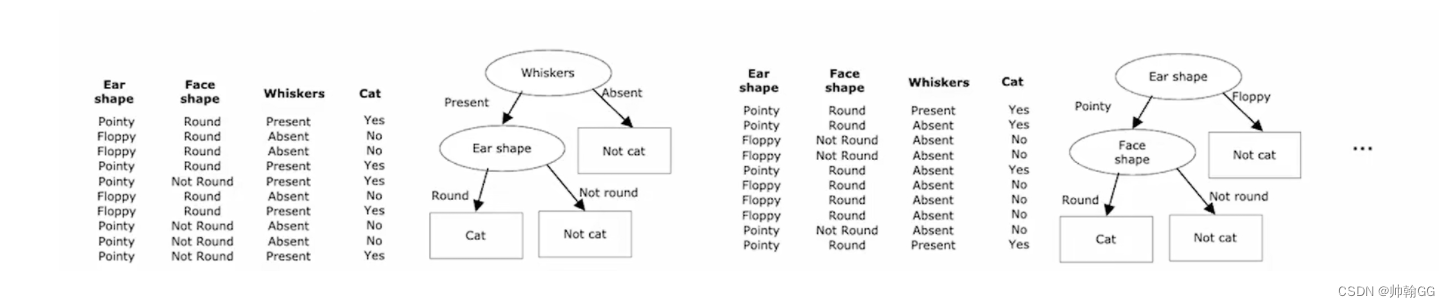
- 举一个例子:
在下图中,我们仅仅改变了一个训练示例,但是由于这个训练示例的改变,造成了 要拆分的 最高 ‘信息增益’——变成了胡子(原来是耳朵的形状)
所以就变成了右侧的决策树,使得左右两侧变成了完全不同的决策树。——训练一堆不同的决策树往往会得到更好的结果——引出 “随机森林”

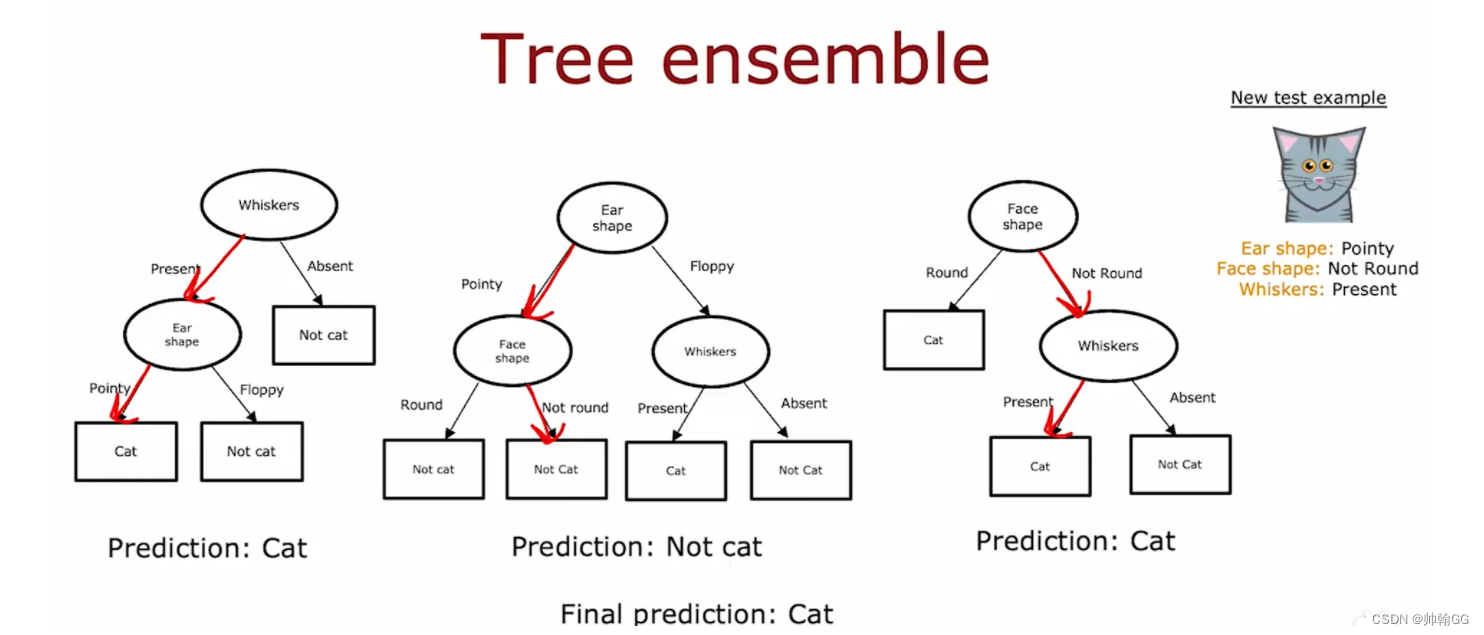
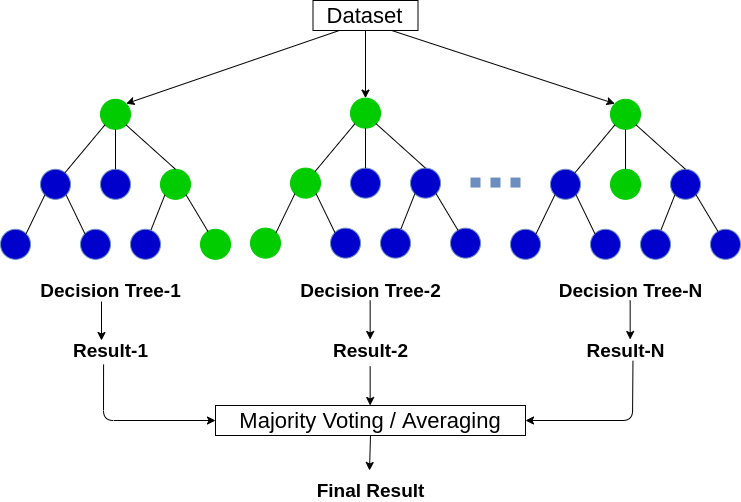
- 多个决策树工作原理:
- 第一个树通过预测——结果是 猫
- 第二个树通过预测——结果不是 猫
- 第三个树通过预测——结果是 猫
最终结果预测:取最多的结果——是猫
随机森林是基于树的机器学习算法,该算法利用了多棵决策树的力量来进行决策。顾名思义,它是由一片树木组成的“森林”!
但是为什么要称其为“随机森林”呢?这是因为它是随机创造的决策树组成的森林。决策树中的每一个节点是特征的一个随机子集,用于计算输出。随机森林将单个决策树的输出整合起来生成最后的输出结果。
简单来说:
“随机森林算法用多棵(随机生成的)决策树来生成最后的输出结果。”
2、随机森林
-
随机森林是由很多决策树组成的,不同决策树之间不存在相关性。
-
当我们执行分类任务时,新的输入样本进入,对森林中的每一棵决策树分别进行判断和分类。每棵决策树都会得到自己的分类结果,而决策树哪个分类结果最多,那么随机森林就会用这个结果作为最终结果。
2.1构建随机森林的 4 个步骤

Ste1:有放回的随机抽样
-
将样本量为N的样本进行N次放回抽取,每次抽取一个样本,最终形成N个样本。将选取的N个样本作为决策树根节点的样本来训练一棵决策树。决策树。
-
如下:是有放回的随机抽样的结果

通过 不同的随机抽样的结果,将选取的N个样本作为决策树根节点的样本来训练一棵决策树。决策树。
不同的随机抽样的 训练集,得到了不同的决策树。
Step2:随机选取属性,作为分裂节点。
- 当每个样本有M(比如100个)个属性时,当决策树的每个节点需要分裂时,从这M个属性中随机选择m(10个)个属性,并满足条件m << M。然后从这些中使用一定的策略(如信息增益) m 个属性,选择 1 个属性作为节点的分裂属性。
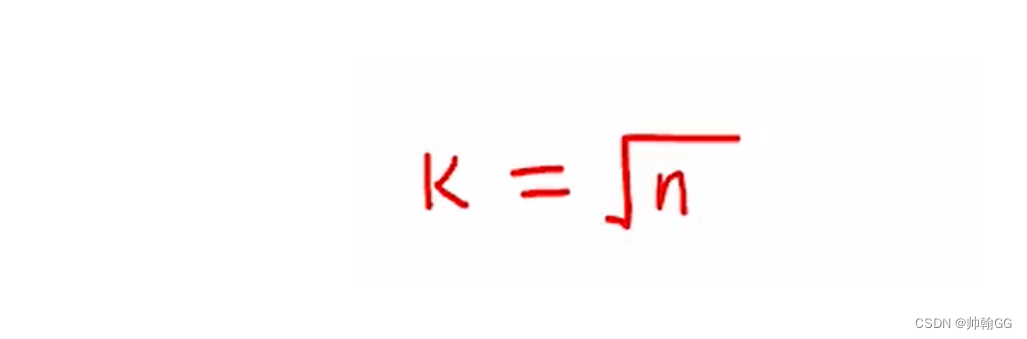
- m 的选择通常如下,就是图中的k :

Step3 :重复步骤2
- 在决策树形成过程中,每个节点都要按照步骤2进行分裂(很容易理解,如果该节点选择的下一个属性是其父节点刚刚分裂时使用的属性,则该节点已经达到叶子节点,无需继续分裂)。直到不能再分开为止。请注意,在整个决策树的形成过程中没有进行任何修剪。
Step4 : 构建随机森林
- 根据步骤1~3,创建大量决策树,构成随机森林。
3、随机森林的4个应用方向——(前提:结构化数据)

随机森连——适用于“结构化数据”
随机森林可以用在很多地方:
- 离散值的分类
- 连续值的回归
- 无监督学习聚类
- 异常点检测
4、※ XGBoot 增强随机森林
- 用的特别多,尤其是在Kaggle比赛等或者实际项目中
- 和 随机森林相比:不同的地方是,随机森林每次都是有放回的抽取(概率是 1/m), 但是 XGBoot 不同,从第二次开始进行针对性的训练。先选取前一轮有错误的数据,再加上随机抽取的数据进行训练。更好的解决问题。