题目：
这是一道LeetCode上的原题：链接地址
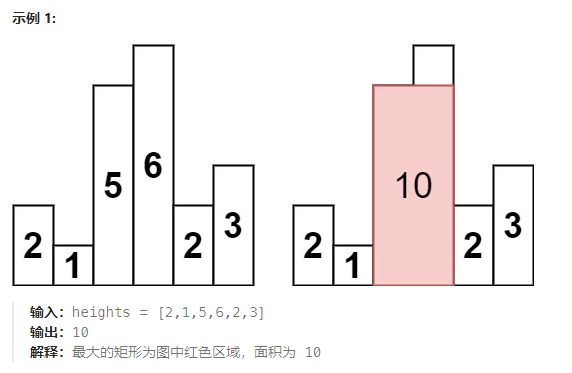
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

思路
因为是力扣原题，所以这道题省略了暴力解和对数器的过程，直接用单调栈的方法写完跑力扣。

整体思路是：遍历数组并维护一个栈底 -> 栈顶是由小到大的单调栈结构。当栈顶元素被弹出后，进行结算。
结算的方式是，以当前弹出元素作为整个矩阵的高，左右向外扩，找到左侧最近且小和右侧最近且小的数作为边界。囊括的中间部分就是以当前高度所形成的矩阵大小。
遍历一遍，以arr[] 中每个数字都作为一次矩阵的高。求max即可。

代码

解释下代码：
cur：是你当前在单调栈中弹出来的数，是满足的上面 if（当前数比栈顶数小） 条件才弹出来的。
所以右侧边界就是当前的 i 。
左侧边界就是弹出后的单调栈的栈顶元素（没有则为-1）。
所以以当前cur为整个矩阵的统一高度，求此时有多少个数。

最后的while，当数组遍历完后，如果栈中不为null，则直接循环弹出栈中元素。
此时，因为数组已经为null，所以不会再有值使栈顶元素弹出，所以右侧没有比当前栈顶元素小的值了。此时栈中剩余元素完全符合由小到大的规则。
所以此时右侧囊括到arr.length。
左侧如果有值，则为左侧最近且小的范围，如果没有，则到 -1。
再次比较大小即可。

public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) {
            return 0;
        }

        Stack<Integer> stack = new Stack<>();
        Integer max = Integer.MIN_VALUE;
        for (int i = 0; i < heights.length; i++) {
            while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
                Integer cur = stack.pop();
                Integer leftMin = stack.isEmpty() ? -1 : stack.peek();
                max = Math.max(max, (i - leftMin - 1) * heights[cur]);
            }
            stack.push(i);
        }
        while (!stack.isEmpty()){
            Integer cur = stack.pop();
            Integer leftMin = stack.isEmpty() ? -1 : stack.peek();
            max = Math.max(max, (heights.length - leftMin - 1) * heights[cur]);
        }
        return max;
    }