一、Qlearning简介
Q-learning是一种强化学习算法,用于解决基于奖励的决策问题。它是一种无模型的学习方法,通过与环境的交互来学习最优策略。Q-learning的核心思想是通过学习一个Q值函数来指导决策,该函数表示在给定状态下采取某个动作所获得的累积奖励。
Q-learning的训练过程如下:
1. 初始化Q值函数,将所有状态-动作对的Q值初始化为0。
2. 在每个时间步,根据当前状态选择一个动作。可以使用ε-greedy策略来平衡探索和利用。
3. 执行选择的动作,并观察环境返回的奖励和下一个状态。
4. 根据Q值函数的更新规则更新Q值。Q值的更新公式为:Q(s, a) = Q(s, a) + α * (r + γ * max(Q(s', a')) - Q(s, a)),其中α是学习率,γ是折扣因子,r是奖励,s是当前状态,a是选择的动作,s'是下一个状态,a'是在下一个状态下选择的动作。
5. 重复步骤2-4,直到达到停止条件。
Q-learning的优点是可以在没有先验知识的情况下自动学习最优策略,并且可以处理连续状态和动作空间。它在许多领域中都有广泛的应用,如机器人控制、游戏策略和交通路线规划等。
二、TSP问题介绍
旅行商问题(Traveling salesman problem, TSP)是一个经典的组合优化问题,它可以描述为一个商品推销员去若干城市推销商品,要求遍历所有城市后回到出发地,目的是选择一个最短的路线。当城市数目较少时,可以使用穷举法求解。而随着城市数增多,求解空间比较复杂,无法使用穷举法求解,因此需要使用优化算法来解决TSP问题。TSP问题的应用非常广泛,不仅仅适用于旅行商问题本身,还可以用来解决其他许多的NP完全问题,如邮路问题、转配线上的螺母问题和产品的生产安排问题等等。因此,对TSP问题的有效求解具有重要意义。解决TSP问题的方法有很多,其中一种常用的方法是蚁群算法。除了蚁群算法,还有其他一些常用的解决TSP问题的方法,如遗传算法、动态规划和强化学习等。这些方法各有特点,适用于不同规模和特征的TSP问题。
三、Qlearning求解TSP问题
1、部分代码
可以自动生成地图也可导入自定义地图,只需要修改如下代码中chos的值即可。
import matplotlib.pyplot as plt
from Qlearning import Qlearning
#Chos: 1 随机初始化地图; 0 导入固定地图
chos=1
node_num=36 #当选择随机初始化地图时,自动随机生成node_num-1个城市
# 创建对象,初始化节点坐标,计算每两点距离
qlearn = Qlearning(alpha=0.5, gamma=0.01, epsilon=0.5, final_epsilon=0.05,chos=chos,node_num=node_num)
# 训练Q表、打印路线
iter_num=1000#训练次数
Curve,BestRoute,Qtable,Map=qlearn.Train_Qtable(iter_num=iter_num)
#Curve 训练曲线
#BestRoute 最优路径
#Qtable Qlearning求解得到的在最优路径下的Q表
#Map TSP的城市节点坐标
## 画图
plt.figure()
plt.ylabel("distance")
plt.xlabel("iter")
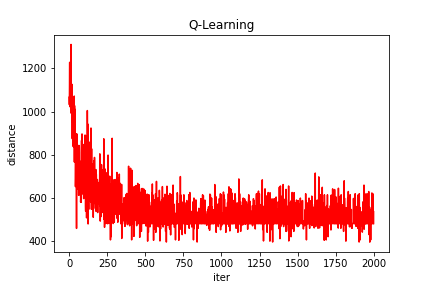
plt.plot(Curve, color='red')
plt.title("Q-Learning")
plt.savefig('curve.png')
plt.show()
2、部分结果
(1)以国际通用的TSP实例库TSPLIB中的测试集bayg29为例:bayg29的城市坐标如下
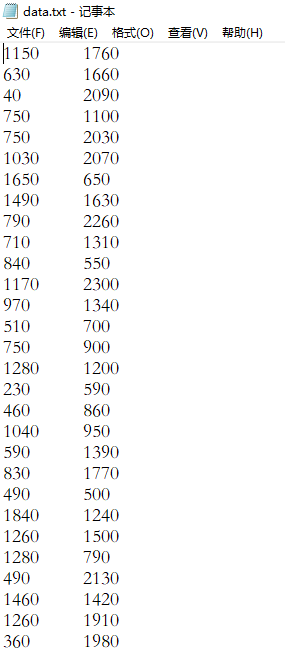


Q-learning得到的最短路线: [1, 28, 6, 12, 9, 3, 29, 26, 5, 21, 2, 20, 10, 4, 15, 18, 14, 22, 17, 11, 19, 25, 7, 23, 27, 8, 24, 16, 13, 1]
(2)随机生成30个城市
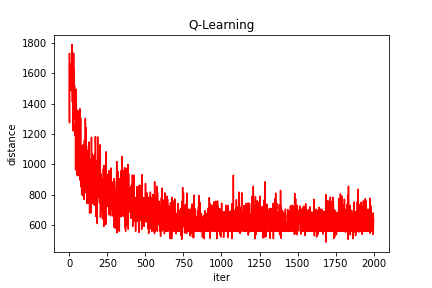
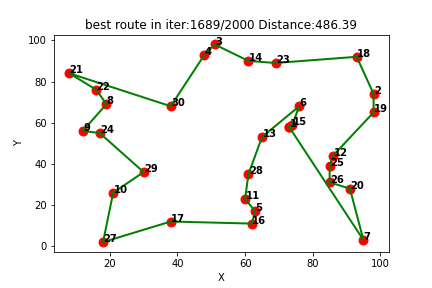
Q-learning得到的最短路线: [1, 15, 6, 13, 28, 11, 5, 16, 17, 27, 10, 29, 24, 9, 8, 22, 21, 30, 4, 3, 14, 23, 18, 2, 19, 12, 25, 26, 20, 7, 1]
(3)随机生成20个城市
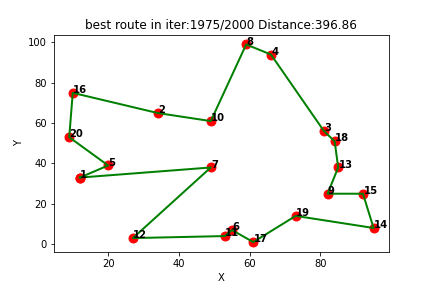
Q-learning得到的最短路线: [1, 5, 20, 16, 2, 10, 8, 4, 3, 18, 13, 9, 15, 14, 19, 17, 6, 11, 12, 7, 1]