个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

力扣递归算法题

 http://t.csdnimg.cn/yUl2I

【C++】    

​​​​​​http://t.csdnimg.cn/6AbpV

数据结构与算法

 ​​​http://t.csdnimg.cn/hKh2l

前言：这个专栏主要讲述动态规划算法，所以下面题目主要也是这些算法做的  

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

下降路径最小和

题目链接：下降路径最小和

题目

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

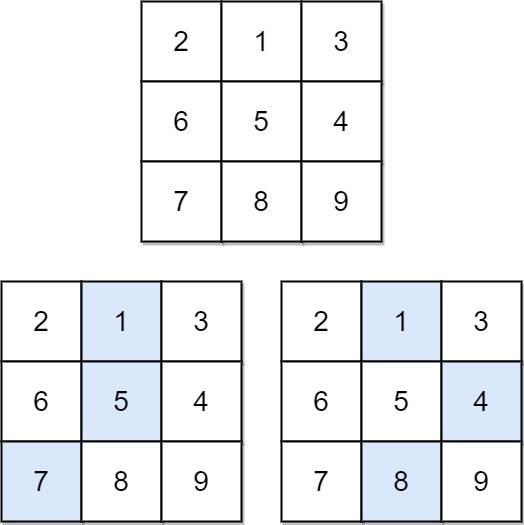
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

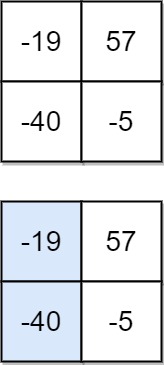
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• -100 <= matrix[i][j] <= 100

解法

题目解析

1. 给你一个mxn的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径的最小和 。
2. 下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。
3. 在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。

算法原理讲解

我们这题使用动态规划，我们做这类题目可以分为以下五个步骤

1. 状态显示
2. 状态转移方程
3. 初始化（防止填表时不越界）
4. 填表顺序
5. 返回值

• 状态显示

• 状态转移方程

• 从正上⽅ [i - 1, j] 位置转移到 [i, j] 位置；
• 从左上⽅ [i - 1, j - 1] 位置转移到 [i, j] 位置；
• 从右上⽅ [i - 1, j + 1] 位置转移到 [i, j] 位置；

• 初始化（防止填表时不越界）

• 填表顺序

根据「状态表⽰」，填表的顺序是「从上往下」。

• 返回值

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) 
    {
        // 1.状态显示---------------》dp[i][j]表示最小路径
        // 2.状态转移方程
        // 3.初始化
        // 4.填表方向
        // 5.返回值


        int n = matrix.size();
        vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));

        // 初始化第一行
        for (int j = 0; j < n + 2; j++)
        {
            dp[0][j] = 0;
        }

        // 填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i - 1][j - 1];
            }
        }

        int ret = INT_MAX;

        for (int i = 1; i <= n; i++)
        {
            ret = min(ret, dp[n][i]);
        }

        return ret;
    }
};