PCA（Principal Component Analysis），中文名称：主成分分析。迄今为止最流行的降维算法。

假设 n 维空间中的一个单位立方体，易知：一维空间中该立方体中任意两点的距离不超过 $1$，二维空间中该立方体中任意两点的距离不超过 $\sqrt{2}$，三维空间中该立方体中任意两点的距离不超过 $\sqrt{3}$，一百万维空间中该立方体中任意两点的距离不超过 $\sqrt{1000000}=1000$。明明是边长为 $1$ 的单位立方体，一百万维空间中的最大距离却有 $1000$，这说明高维空间中的数据是非常稀疏的。

PCA 可以识别哪些维度上的信息量最高（主要成分），并将数据投影到那些有着最高信息量维度表示的平面上。PCA 使用 SVD （奇异值分解）找到数据的主要成分。

比如说有 100 个三维空间中的数据 $A_{100\times 3}$（假设数据以原点为中心，如果不是先将数据居中，这是为了消除数据的均值影响，确保主成分的计算是基于数据的奇异性而不是均值），对其使用 SVD 分解：
$$U_{100\times 100}\cdot S_{100\times 3}\cdot V_{3\times 3}^T=A_{100\times 3}$$
其中 $U,V$ 分别是左右奇异阵，为正交阵，$S$ 是奇异值阵，为对角阵。

要将数据降为多少维，就保留 $V$ 的前几列，再将 $A$ 与其相乘，就得到了降维后的数据。

如将三维空间数据集 $A$ 降为 $2$ 维，就保留 $V$ 的前两列，设
$$W=V(:,1:2)$$
则降维后的数据为：
$$A_{reduced}=A\cdot W$$
将降维后的数据恢复原来的维度：
$$A_{recovered}=A_{reduced}\cdot W^T$$
恢复后的 $A_{recovered}\ne A$，因为 $W\cdot W^T\ne I$。这会损失掉 $A$ 的一部分信息。

另外可以通过 $S$ 矩阵知道降维后的数据保留了多少信息量。比如说 $S$ 矩阵为

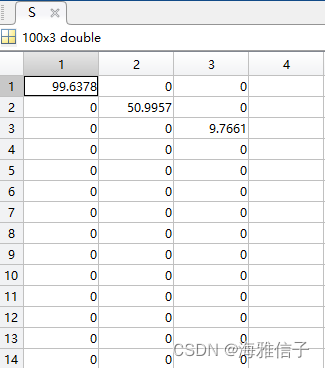
即每一维的信息比为

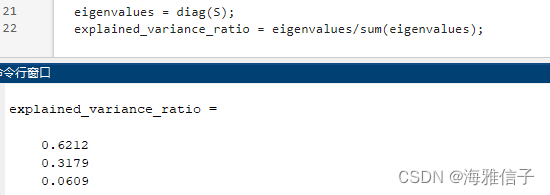
将 $A$ 降为 $2$ 维，降维后的数据保留了 $A$ 中 $93.91\%$ 的信息。
代码如下：

% created by hyacinth on 2024/1/9
clc
clear
close all

%%
A1 = 10*randn(100,1);
A2 = 5*randn(100,1);
A3 = randn(100,1);

A = [A1,A2,A3];
A = A - mean(A);

[U,S,V] = svd(A);

newdim = 2;
W = V(:,1:newdim);

A_reduced = A*W;
A_recovered = A_reduced*W';

eigenvalues = diag(S);
explained_variance_ratio = eigenvalues/sum(eigenvalues);
info_ratio = sum(explained_variance_ratio(1:newdim));
disp("the retained information ratio is : "+num2str(info_ratio))