动态规划
动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利用已经计算好的小问题的解,而不需要重复计算。
动态规划与数学归纳法思想上十分相似。
数学归纳法:
-
基础步骤(base case):首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况,可以直接验证命题是否成立。
-
归纳步骤(inductive step):假设命题在某个情况下成立,然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。
通过反复迭代归纳步骤,我们可以推导出命题在所有情况下成立的结论。
动态规划:
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
数学归纳法的基础步骤相当于动态规划中初始化步骤。
数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。
动态规划的思想和数学归纳法思想类似。
在动态规划中,首先得到状态在最小的基础情况下的值,然后通过状态转移方程,得到下一个状态的值,反复迭代,最终得到我们期望的状态下的值。
接下来我们通过三道例题,深入理解动态规划思想,以及实现动态规划的具体步骤。
518. 零钱兑换 II - 力扣(LeetCode)
题目解析

状态表示
这个问题本质上是,
-
从一些数中挑选一些数出来,然后再满足某些限定条件下,解决一些问题。而背包问题就是用来解决组合问题。
-
每一个物品都是无限多个,因此属于完全背包问题。
完全背包实际上是一个模版,我们根据完全背包的状态表示,去定义我们希望得到的状态表示。
完全背包的状态表示是,
定义dp[i][j]表示从前i个物品中挑选,总体积不超过j,所有选法中,所能达到的最大价值。
定义dp[i][j]表示从前i个物品中挑选,总体积恰好为j,所有选法中,所能达到的最大价值。
因此我们可以定义dp[i][j]表示从前i个硬币中挑选,总和正好为j,一共有多少种选法。
状态转移方程
根据最后一个位置的具体情况进行分类讨论。
-
如果选择0个第i个硬币, 此时相当于在前i-1个硬币中挑选,总和正好为j,一共有多少种选法。此时dp[i][j]=dp[i-1][j]。
-
如果选择1个第i个硬币, 此时相当于,在前i-1个硬币中挑选,总和正好为j-coins[i],一共有多少种选法,在这些选法中,把1个第i个硬币放进去,此时的选法就等于在前i个硬币中挑选,总和正好为j,而这时候有多少种选法呢?有dp[i-1][j-coins[i]]种选法,此时dp[i][j]=dp[i-1][j-coins[i]]。
-
如果选择2个第i个硬币, 此时相当于,在前i-1个硬币中挑选,总和正好为j-2*coins[i],一共有多少种选法,在这些选法中,把2个第i个硬币放进去,此时的选法就等于在前i个硬币中挑选,总和正好为j,而这时候有多少种选法呢?有dp[i-1][j-2*coins[i]]种选法,此时dp[i][j]=dp[i-1][j-2*coins[i]]。
-
............
-
一直到全部选择第i个硬币为止。
综上所述,dp[i][j]=dp[i-1][j]+dp[i-1][j-coins[i]]+dp[i-1][j-2*coins[i]]+.........
我们发现一个很有趣的东西,等式的右边,横坐标不变,纵坐标依次减少coins[i],因此我们可以尝试推导dp[i][j-coins[i]]。
dp[i][j-coins[i]]=dp[i-1][j-coins[i]]+dp[i-1][j-2*coins[i]]+........,而
dp[i][j]=dp[i-1][j]+dp[i-1][j-coins[i]]+dp[i-1][j-2*coins[i]]+.........,
因此我们可以把dp[i][j]写成这样,dp[i][j]=dp[i-1][j]+dp[i][j-coins[i]];
这样我们就将O(n)减低成O(1)。
而上述coins[i]表示的并不是表示第i个硬币,因为coins[0]表示第一个硬币,所以第i个硬币应该是coins[i-1]表示第i个硬币,所以,状态转移方程应该为,dp[i][j]=dp[i-1][j]+dp[i][j-coins[i-1]];
综上所述,状态转移方程为,
dp[i][j] = dp[i - 1][j];
if (j - coins[i - 1] >= 0)
dp[i][j] += dp[i][j - coins[i - 1]];初始化
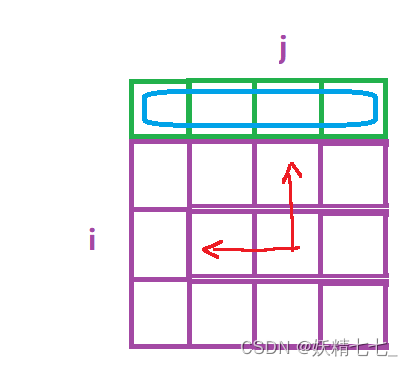
根据状态转移方程,我们知道在推导(i,j)位置状态的时候,需要用到(i-1,j)(i,j-coins[i-1])位置的状态。而使用(i,j-coins[i-1])状态时,j-coins[i-1]>=0,此时一定不会越界,所以我们只需要考虑(i-1,j)位置状态即可。
在蓝色部分,即第一行,会发生越界的情况,此时初始化这些位置的状态时,没有前驱状态值,所以我们需要初始化这些位置的状态。
第一行i==0,表示不选择硬币,硬币总和为j,一共的选法,此时(0,0)位置为1,即不选一种方法,而其他位置都为0,没有选法可以达到。其他位置是不存在,而不存在正常来说要用特殊的标志表示,但是在这道题中,用0表示不存在也不会有影响。所以不存在也用0表示。
综上所述,初始化为,
dp[0][0] = 1;填表顺序
根据状态转移方程,我们知道在推导(i,j)位置状态的时候,需要用到(i-1,j)(i,j-coins[i-1])位置的状态。
-
固定i改变j, i的变化需要从小到大,因为可能要用到(i,j-coins[i-1])的状态,所以j的变化也需要从小到大。
-
固定j改变i, j的变化需要从小到大,因为可能要用到(i-1,j)位置的状态,所以i的变化也需要从小到大。
返回值
状态表示为,定义dp[i][j]表示从前i个硬币中挑选,总和正好为j,一共有多少种选法。
结合题目意思,我们要返回,从前n个硬币中挑选,总和正好为m,一共有多少种选法。
故返回dp[n][m],(m为amount)
代码实现
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
int m = amount;
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
dp[i][j] = dp[i - 1][j];
if (j - coins[i - 1] >= 0)
dp[i][j] += dp[i][j - coins[i - 1]];
}
}
return dp[n][m];
}
};279. 完全平方数 - 力扣(LeetCode)

题目解析

状态表示
这个问题本质上是,
-
从一些数中挑选一些数出来,然后再满足某些限定条件下,解决一些问题。而背包问题就是用来解决组合问题。
-
每一个物品都是无限多个,因此属于完全背包问题。
完全背包实际上是一个模版,我们根据完全背包的状态表示,去定义我们希望得到的状态表示。
完全背包的状态表示是,
定义dp[i][j]表示从前i个物品中挑选,总体积不超过j,所有选法中,所能达到的最大价值。
定义dp[i][j]表示从前i个物品中挑选,总体积恰好为j,所有选法中,所能达到的最大价值。
因此我们可以定义dp[i][j]表示从前i个数的完全平方数中挑选,总和正好为j,完全平方数的最少数量。
状态转移方程

根据最后一个位置的具体情况进行分类讨论。
-
如果选择0个第i个数的完全平方数, 此时相当于在前i-1个数的完全平方数中挑选,总和正好为j,这种情况下完全平方数的最少数量,此时dp[i][j]=dp[i-1][j]。i
-
如果选择1个第i个数的完全平方数, 此时相当于在前i-1个数的完全平方数中挑选,总和正好为j-i^2,完全平方数的最少数量,此时再加上1个第i个数的完全平方数,相当于在前i个数的完全平方数中挑选,总和正好为j,这种情况下完全平方数的最少数量,即dp[i][j]=dp[i-1][j-i^2]+1。
-
如果选择2个第i个数的完全平方数, 此时相当于在前i-1个数的完全平方数中挑选,总和正好为j-2*i^2,完全平方数的最少数量,此时再加上2个第i个数的完全平方数,相当于在前i个数的完全平方数中挑选,总和正好为j,这种情况下完全平方数的最少数量,即dp[i][j]=dp[i-1][j-2*i^2]+2。
-
..........
-
一直到全部选择第i个数的完全平方数。
综上所述,dp[i][j]=min(dp[i-1][j],dp[i-1][j-i^2]+1,dp[i-1][j-2*i^2]+2,.........)
我们发现一个很有趣的东西,等式右边,横坐标不变,纵坐标依次减少i^2。因此我可以尝试推导dp[i][j-i^2]。
得到dp[i][j-i^2]=min(dp[i-1][j-i^2],dp[i-1][j-2*i^2]+1,dp[i-1][j-3*i^2]+2,........)
为了统一,dp[i][j-i^2]+1=min(dp[i-1][j-i^2]+1,dp[i-1][j-2*i^2]+2,dp[i-1][j-3*i^2]+3,........)
又dp[i][j]=min(dp[i-1][j],dp[i-1][j-i^2]+1,dp[i-1][j-2*i^2]+2,.........)
故可以将dp[i][j]写成这样,dp[i][j]=min(dp[i-1][j],dp[i][j-i^2]+1);
当dp[i-1][j]或者dp[i][j-i^2]不存在的时候,不能选到了他们,因此我们可以将不存在定义为INF=0x3f3f3f3f,因为是取两者小的一个,所以即使不存在也不会取到他们。
综上所述,状态转移方程为,
dp[i][j] = dp[i - 1][j];
if (j - i * i >= 0)
dp[i][j] = min(dp[i][j], dp[i][j - i * i] + 1);初始化

根据状态转移方程,我们知道在推导(i,j)位置的状态时,需要用到(i-1,j)(i,j-i^2)的状态。
而用(i,j-i^2)的状态时,j-i^2一定不会越界,所以我们只需要考虑(i-1,j)的状态即可。
因此在推导第一行的状态时,会发生越界的情况,此时没有前驱状态值,所以我们需要初始化第一行的状态。
第一行,i==0,表示不选数,总和为j,平方数的个数,(0,0)位置状态应该初始化为0,其他位置状态为不存在,我们根据前面的分析,得出不存在应该初始化为0x3f3f3f3f。
填表顺序
根据状态转移方程,我们知道在推导(i,j)位置的状态时,需要用到(i-1,j)(i,j-i^2)的状态。
-
固定i,改变j, i的变化需要从小到大,因为要使用到(i,j-i^2)位置状态,所以j的变化也需要从小到大。
-
固定j,改变i, j的变化需要从小到大,因为要使用到(i-1,j)位置状态,所以i的变化也需要从小到大。
返回值
根据状态表示定义dp[i][j]表示从前i个数的完全平方数中挑选,总和正好为j,完全平方数的最少数量。
结合题目要求,我们需要返回,从前m个数的完全平方数中挑选,总和正好为n,完全平方数的最少数量。
(m的完全平方数应该小于等于n,而m+1的完全平方数>n)
返回dp[m][n];
代码实现
class Solution {
public:
int numSquares(int n) {
int m = 1;
while (m * m <= n)
m++;
m--;
int INF = 0x3f3f3f3f;
vector<vector<int>> dp(m + 1, vector<int>(n + 1, INF));
dp[0][0] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 0; j <= n; j++) {
dp[i][j] = dp[i - 1][j];
if (j - i * i >= 0)
dp[i][j] = min(dp[i][j], dp[i][j - i * i] + 1);
}
}
return dp[m][n];
}
};474. 一和零 - 力扣(LeetCode)

题目解析

状态表示
这个问题本质上是,
-
从一些数中挑选一些数出来,然后再满足某些限定条件下,解决一些问题。而背包问题就是用来解决组合问题。
-
每一个物品都是无限多个,因此属于完全背包问题。
完全背包实际上是一个模版,我们根据完全背包的状态表示,去定义我们希望得到的状态表示。
完全背包的状态表示是,
定义dp[i][j]表示从前i个物品中挑选,总体积不超过j,所有选法中,所能达到的最大价值。
定义dp[i][j]表示从前i个物品中挑选,总体积恰好为j,所有选法中,所能达到的最大价值。
因此我们可以定义dp[i][j][k]表示从前i个字符串中挑选,字符0的个数不超过j,字符1的个数不超过k,所有选法中,子集的最大个数。
状态转移方程
根据最后一个位置的具体情况进行分类讨论。
假设第i个字符串中,字符0的个数为a,字符1的个数为b。
-
不选第i个字符串, 相当于在前i-1个字符串里面挑选,使字符0的个数不超过j,字符1的个数不超过k,所有选法中,子集的最大个数。此时dp[i][j][k]=dp[i-1][j][k];
-
挑选第i个字符串, 那么接下来,我需要在前i-1个字符串里面挑选出一些字符串,使得字符0的个数不超过j-a,字符1的个数不超过k-b,然后在这些字符串中加入第i个字符串,此时相当于在前i个字符串里面挑选出一些字符串,使得字符0的个数不超过j,字符1的个数不超过k。此时dp[i][j][k]=dp[i-1][j-a][k-b]+1。
综上所述,状态转移方程为,
dp[i][j][k]=max(dp[i-1][j][k],dp[i-1][j-a][k-b]+1)需要推导(i,j,k)位置的状态,需要用到(i-1,j,k)(i-1,j-a,k-b)位置的状态,使用前提就是不能越界,对于(i-1,j,k)可以初始化第一行处理,而对于(i-1,j-a,k-b)初始化不好处理,所以我们选择直接考虑其存在的情况,即if(j>=a&&k>=b)才使用。
因此状态转移方程可以写成,
dp[i][j][k] = dp[i - 1][j][k];
if (j >= a && k >= b)
dp[i][j][k] =
max(dp[i][j][k], dp[i - 1][j - a][k - b] + 1);初始化
根据状态转移方程,我们知道想要推导(i,j,k)位置的状态时,需要用到(i-1,j,k)(i-1,j-a,k-b)位置的状态。而(i-1,j-a,k-b)位置的状态的使用,我们已经考虑过j-a,和k-b不越界的情况,所以我们只需要考虑i-1以及(i-1,j,k)位置状态不越界的情况。
因此我们需要初始化i==0的情况。
当i==0时,表示不选字符串,字符0个数不超过j,字符1的个数不超过k,所有情况中,字符串个数最大值。所以i==0时,所有位置状态应该为0。
填表顺序
根据状态转移方程,我们知道想要推导(i,j,k)位置的状态时,需要用到(i-1,j,k)(i-1,j-a,k-b)位置的状态。
-
固定i,改变j,改变k i的变化需要从小到大,j、k的变化可以从小到大也可以从大到小。因为i从小到大变化,就满足了在推导(i,j,k)位置状态时,(i-1,,)的状态已经得到。
-
固定j,改变i,改变k j的变化需要从小到大,因为需要用到(i-1,j,k)位置的状态,所以i的变化需要从小到大,k的变化可以从小到大也可以从大到小。
-
固定k,改变i,改变j k的变化需要从小到大,因为需要用到(i-1,j,k)位置的状态,所以i的变化需要从小到大,j的变化可以从小到大也可以从大到小。
这三种情况,后面的顺序都可以交换。
返回值
状态表示定义dp[i][j][k]表示从前i个字符串中挑选,字符0的个数不超过j,字符1的个数不超过k,所有选法中,子集的最大个数。
结合题目意思,我们需要从前len个字符串中挑选,字符0的个数不超过m,字符1的个数不超过n,所有选法中,子集的最大个数。所以我们需要返回dp[len][m][n],(len是strs中字符串的个数)
代码实现
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int len = strs.size();
vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(m + 1, vector<int>(n + 1)));
for (int i = 1; i <= len; i++) {
int a = 0, b = 0;
for (auto ch : strs[i - 1])
if (ch == '0')
a++;
else
b++;
for (int j = m; j >= 0; j--)
for (int k = n; k >= 0; k--) {
dp[i][j][k] = dp[i - 1][j][k];
if (j >= a && k >= b)
dp[i][j][k] =
max(dp[i][j][k], dp[i - 1][j - a][k - b] + 1);
}
}
return dp[len][m][n];
}
};结尾
今天我们学习了动态规划的思想,动态规划思想和数学归纳法思想有一些类似,动态规划在模拟数学归纳法的过程,已知一个最简单的基础解,通过得到前项与后项的推导关系,由这个最简单的基础解,我们可以一步一步推导出我们希望得到的那个解,把我们得到的解依次存放在dp数组中,dp数组中对应的状态,就像是数列里面的每一项。最后感谢您阅读我的文章,对于动态规划系列,我会一直更新,如果您觉得内容有帮助,可以点赞加关注,以快速阅读最新文章。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!