1．解释众数、中位数和调和平均数。

（1）众数：一组数据中出现频数最多的变量值，用M0表示
（2）中位数：一组数据排序后处于最中间位置的变量值，用Me表示
（3）调和平均数：又称 “ 倒数平均数 ” ，是各变量值的倒数的算数平均数的倒数，用H表示

2、什么是普查？其有何特点和作用？

普查：
是为了某种特定目的而专门组织的一次性全面调查
特点：
（1）普查通常是一次性的或周期性的
（2）普查一般需要规定统一的标准调查时间，以确保普查结果的准确性，避免调查数据的重复与遗漏
（3）普查的数据一般比较准确，标准化程度也比较高，可为其他调查方式提供基本的参照依据，特别是能与抽样调查的数据资料相互验证，以提高调查质量，保证调查精度在合理范围之内
（4）普查适用的范围比较狭窄，只能调查一些最基本、最一般的现象

3、什么是抽样调查？其有何特点和作用？

抽样调查：
是对样本基本单位进行调查的一种专门组织的非全面调查
特点和作用：
代表性：
通过合理的抽样方法，样本应该能够准确地代表总体的特征，通过对样本的研究和分析，我们可以推断出总体的一些特征
节省成本和时间：
选择一个相对较小的样本，研究者可以在更短的时间内完成数据收集和分析，并得出结论。这对于大规模调查或研究项目来说特别有用
可控性和可操作性：
选择适当的抽样方法，并确定样本的大小。可以更好地控制调查的范围和精度，并确保数据的准确性和可靠性
统计推断：
抽样调查是进行统计推断的基础。通过对样本数据进行分析，可以通过估计总体参数、计算置信区间、进行假设检验等方式来实现
描述和解释：
抽样调查可以用于描述和解释总体的特征和行为。研究者可以获得关于总体的定量或定性信息，并从中提取有关总体特征的洞察。这有助于我们理解市场、社会现象等的特点和变化

4、什么是偏度系数，并解释左偏分布、对称分布和右偏分布。

偏度系数是变量的三阶中心矩与其标准差的三次方对比的结果，用a表示，反映分布的不对称方向和程度，公式：a = m3/o^3
右偏分布：偏度系数a>0
对称分布：偏度系数a=0
左偏分布：偏度系数a<0

5、解释置信区间、置信度和显著性水平。

置信度区间：
就是变量的一个范围，变量落在这个范围的可能性就是1-a
置信度：
就是相信变量在设定的置信区间的程度，是个0~1之间的数，用1-a表示
显著性水平：
变量落在置信度区间以内的可能性，“显著”就是设想的置信区间一样，用a表示

6、什么是回归分析？其步骤是什么？

回归分析：
是根据已知变量估计未知变量的一种统计方法，它是以对未知变量（因变量）同其他变量（自变量）相互关系的观察为基础，在某种精度下，预测未知变量的数值
步骤：
（1）选择适当的回归模型，根据理论分析所研究的客观现象，找出其现象间的因果关系及相互之间的联系，构建理论模型，来得到更好地反映客观现象变化规律的回归模型，还可根据相关关系的具体形态或散点图的方法选择一个拟合效果较好的回归模型
（2）对收集的样本数据，对模型中的参数进行参数估计
（3）对参数估计值加以评定，确定他们在理论上是否有意义，是否显著，只有通过检验的模型才能实际应用
（4）根据回归方程进行适当的预测

7、什么是相关关系？相关系数如何计算，它有哪些特点？

相关关系：
指现象之间客观存在的非确定性的数量依存关系
如何计算：

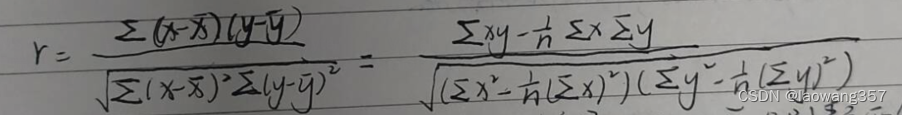
r表示相关系数，x和y分别表示两个变量
特点：
是描述相关的两个变量之间相关关系密切程度的数量指标

8、第一类错误和第二类错误分别是什么？它们发生的概率大小之间有什么关系？

第一类错误：
当原假设为真时拒绝原假设，又称“弃错误”，错误的概率常记为“阿法（a）”
第二类错位：
当原假设为假时拒绝原假设，又称“伪错误”，错误概率常记为“贝塔（B）”
他们发生的概率大小关系：

当a增大时B减小，B增大时a减小

9．进行方差分析时，需要哪几个基本假定？

需要三个基本假设：
（1）每个总体都应该服从正态分布。对于因素的每个水平，其观察值是来自正态分布的简单随机样本
（2）各总体的方差o^2必须相同。对于各组观察数据，是从具有相同方差的正态总体中抽取
（3）观察值是独立的。

10．什么是拉氏指数？请写出拉氏物量指数公式。

拉氏指数：
是将同度量因素固定在基期，是为了单纯地反映指数变化因素的综合变动
拉氏物量指数公式：