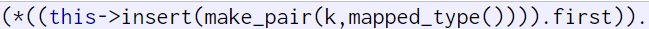为什么LU分解中的下三角矩阵L的主对角线上都是1?

笔者的一些话：

        为什么LU分解中L矩阵的主对角线上都是1？因为最近一段时间在研究LU分解的编程实现，这个问题也就时不时的从我脑子里面冒出来。但大多时候都是一闪而过，没有太在意。有时候，查了一些资料后，明白了，或者是当时明白了，又或者是似乎明白了，没过多久又忘了。索性趁着这两天有空，干脆写一篇CSDN记录下来，自己以后要看了，就回来翻翻。

正文：

        一方面：对于LU分解而言，下三角阵L是对高斯消元过程的记录，是高斯消元的逆过程，是多个消元矩阵E的逆矩阵的乘积(形如下图中的下三角矩阵)，即：

        另一方面：根据矩阵的乘法原则，两个矩阵A和B的乘积C中的元素，来自于矩阵A中第i行元素与矩阵B中第j列元素的乘积。下图，是我引用的维基百科中一个4x2矩阵A和一个2x4矩阵B的乘法的说明图。

如图，在本例中矩阵C中的元素源自于矩阵A第一行和矩阵B第二列的乘积。 

        按照这个乘法规则，去计算一系列消元矩阵的逆矩阵(方阵)的乘法就会发现。在计算L矩阵中主对角线上元素时，其他部分的乘积都是0，最终只剩下主对角线上对应位置的乘积为1。

比如说，下面是两个4x4的矩阵的乘法(X和Y可以是任意值)：

        不论这两个矩阵中的X和Y是多少，主对角线上的元素一定是1。我们以的计算为例(其他也相仿)，他等于前一个矩阵的第2行，乘以后一个矩阵的第2列：

        

        依此类推，则不论有多少个 连续相乘，一定能保证在最终的乘积L矩阵中，主对角线上的元素都是1。

---

（全文完）

作者 --- 松下J27 

 参考文献(鸣谢)：

1，https://en.wikipedia.org/wiki/Matrix_multiplication

2，线性代数 --- LU分解（Gauss消元法的矩阵表示）_矩阵的lu分解-CSDN博客

（配图与本文无关） 

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27