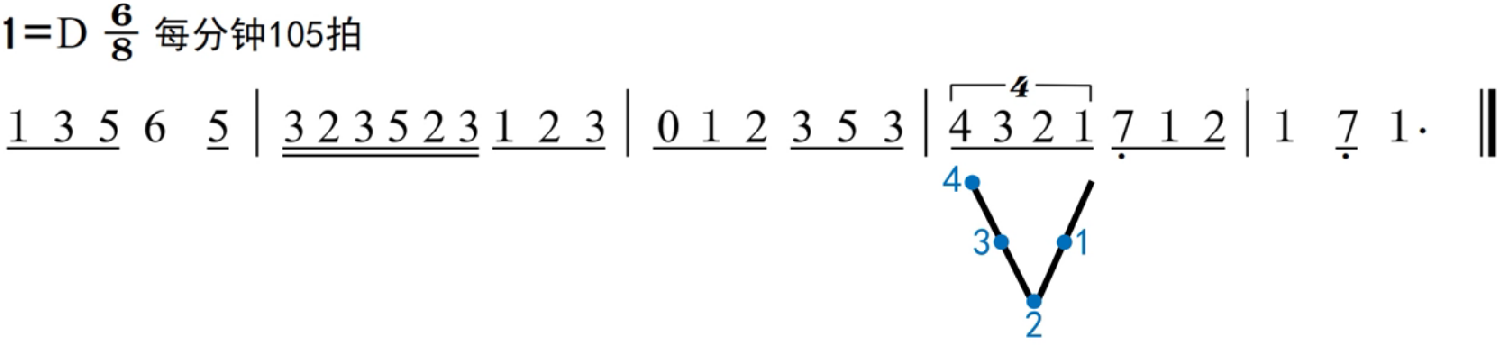我们在CUDA中使用设备内存方面有一个内在的权衡：全局内存大但速度慢，而共享内存小但速度快。一个常见的策略是将数据划分为称为tile的子集，以便每个tile都适合共享内存。tile一词”借鉴了一个类比，即大墙（即全局内存数据）可以被瓷砖覆盖（即每个可以放入共享内存的子集）。一个重要的标准是，这些tile上的内核计算可以相互独立执行。请注意，给定任意内核函数，并非所有数据结构都可以分区为tile。

tile的概念可以使用图4.5中的矩阵乘法示例来说明，对应于图4.3.中的内核函数。我们复制了图4.9 中的示例。方便读者参考。为了简洁，我们使用Py，X，My，X和Ny，x分别表示P[yWidth+ x], M[yWidth+ x]和N[y*Width+ x]。这个例子假设我们使用四个2x2块来计算P矩阵。图4.9突出显示由块（0,0）的四个线程执行的计算。这四个线程计算P0,0,P0,1,P1,0和P1,1。块（0,0）的线程（0,0）和线程（0,1）访问M和N元素的访问用黑色箭头突出显示；例如，线程（0,0）读取Mo.o和No.o.，然后是Mo.1和Ni.o.，然后是Mo.2和N2.0，然后是Mo.3和N3.0。

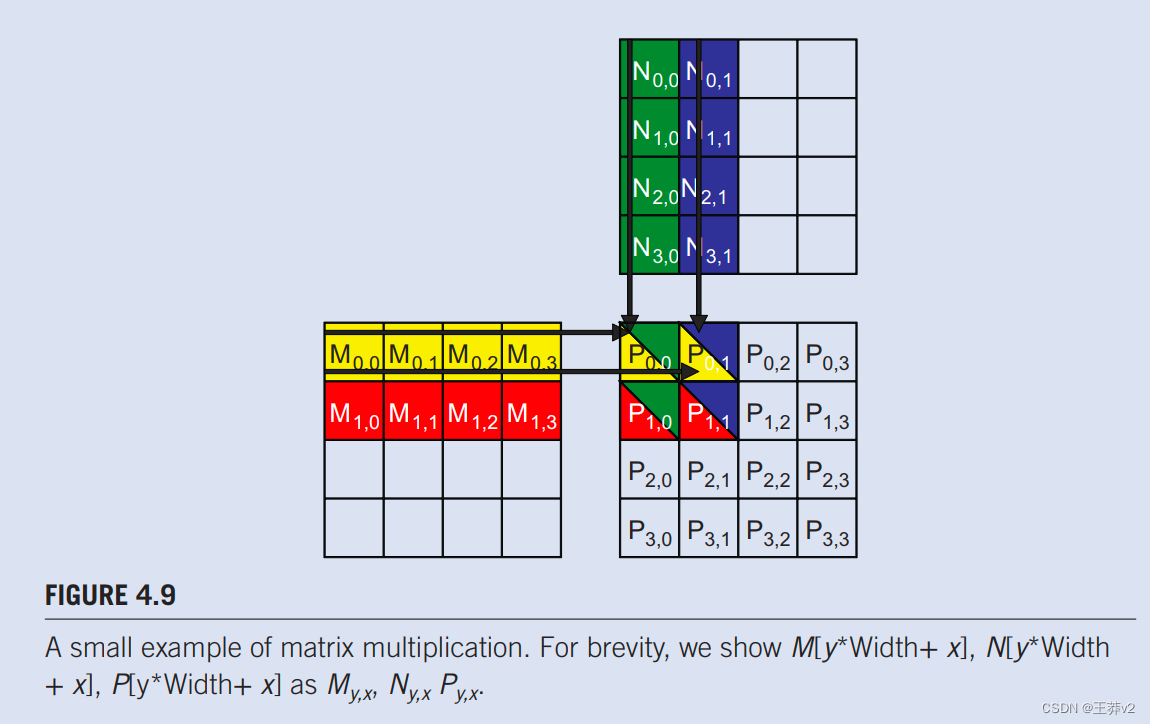
图4.10显示block0.0中所有线程执行的全局内存访问。线程以垂直方向列出，访问时间增加到就在水平方向。在执行过程中，每个线程访问M的四个元素和N的四个元素。在突出显示的四个线程中，它们访问的M和N元素发生了明显的重叠。例如，thread0.0和thread0,1都访问M0.0和M行0的其余部分。同样，thread0,1和thread1,1都访问N 0,1 和N第1列的其余部分。

图4.3中的内核的编写使thread0.0和thread0.1都从全局内存中访问M的行0元素。如果可以使thread0.0和thread0,1进行协作，以便这些M元素只能从全局内存加载一次，则对全局内存的访问总数可以减少一半。在执行block0.0期间，每个M和N元素都会被准确访问两次。因此，如果所有四个线程都可以在访问全局内存时进行协作，则到gobal内存的流量可以减少一半。

读者应验证矩阵乘法示例中全局内存流量的潜在减少与所用块的维度成正比。使用宽度×宽度块，全局内存流量的潜在减少将是宽度。因此，如果我们使用16×16块，通过线程之间的协作，全局内存轨道可能会减少到1/16。

交通拥堵不仅出现在计算中，也出现在高速公路系统中，如图4.11.所示。高速公路交通拥堵的根本原因是太多的汽车挤过一条为数量少得多的车辆设计的道路。当发生拥堵时，每辆车的旅行时间会大大增加。在交通拥堵期间，上下班时间很容易增加一倍或三倍。

大多数减少交通拥堵的解决方案都涉及减少道路上的汽车。假设通勤者的数量是恒定的，人们需要共享游乐设施，以减少道路上的汽车数量。在美国，共享游乐设施的一种常见方式是拼车，一群通勤者轮流驾驶这群人乘坐一辆车工作。政府通常需要制定鼓励拼车的政策。在一些国家，政府只是每天禁止某些类别的汽车上路。例如，周一、周三或周五，车牌奇怪的汽车可能不允许上路。这项规则鼓励在不同日期允许汽车的人组成拼车小组。在一些国家，汽油价格如此之高，以至于人们拼车来省钱。在其他国家，政府可能会为减少道路上汽车数量的行为提供激励措施。在美国，一些拥堵的高速公路车道被指定为拼车车道；只有超过两到三人的汽车才能使用这些车道。所有这些鼓励拼车的措施都是为了克服拼车需要额外努力的事实，如图4.12.所示。

拼车要求希望拼车的工人妥协并就共同的通勤时间表达成一致。图4.12的上半部分为拼车提供了良好的时间表模式。时间从左到右。工人A和B共享类似的睡眠、工作和晚餐时间表。这个时间表允许这两名工人方便地去上班，然后用一辆车回家。他们类似的时间表使他们能够轻松商定共同的出发和返回时间。相比之下，图的下半部分的时间表。4.12显示工人A和B有不同的习惯：工人A聚会到日出，白天睡觉，晚上去上班；工人B晚上睡觉，早上去上班，下午6点回家吃晚饭。时间表非常不同，以至于这两个工人无法安排一个共同的时间开车去上班，然后开着一辆车回家。为了让这些工人组成拼车，他们需要协商一个类似于图4.12.上半部分的共同时间表。

Tiled算法与拼车安排非常相似。我们可以将线程访问数据值视为通勤者，将DRAM访问请求视为车辆。当DRAM请求的速率超过DRAM系统的预置访问带宽时，就会出现流量拥塞**，算术单元变得空闲。如果多个线程从同一DRAM位置访问数据，它们可能会形成“拼车”，并将其访问合并到一个DRAM请求中**。然而，这个过程需要对线程进行类似的执行计划，以便可以合并其数据访问。此场景如图4.13所示，其中中心的单元格代表DRAM位置。指向线程的DRAM位置的箭头表示线程在箭头标记的时间访问该位置。请注意，时间从左到右。顶部显示两个线程，这些线程以相似的时间访问相同的数据元素。下半部分显示了两个在不同时间访问其公共数据的线程；即，线程2的访问明显落后于线程1的相应访问。底部是一个不可取的安排的原因是，从DRAM带回的数据元素需要长时间存储在芯片内存中，等待被线程2消耗。需要存储大量数据元素，导致片上内存需求过高。

**在并行计算的背景下，tiling是一种程序转换技术，可以本地化线程之间访问的内存位置及其访问的时间。它将每个线程的长访问序列分为阶段，并使用屏障同步来保持每个部分的访问时间间隔。**这项技术通过在时间和空间中本地化访问来控制所需的片上内存量。就我们的拼车类比而言，我们迫使组成“拼车”组的线程遵循大致相同的执行时间。

我们现在提出了一个tiling矩阵乘法算法。**基本想法是线程在点积计算中单独使用这些元素之前，协同将M和N元素的子集加载到共享内存中。**共享内存的大小非常小，当这些M和N元素加载到共享内存中时，不应超过共享内存的容量。这个条件可以通过将M和N矩阵分成更小的tile来满足，这样它们就可以适应共享内存。以最简单的形式，tile尺寸等于块的尺寸，如图4.11.所示。

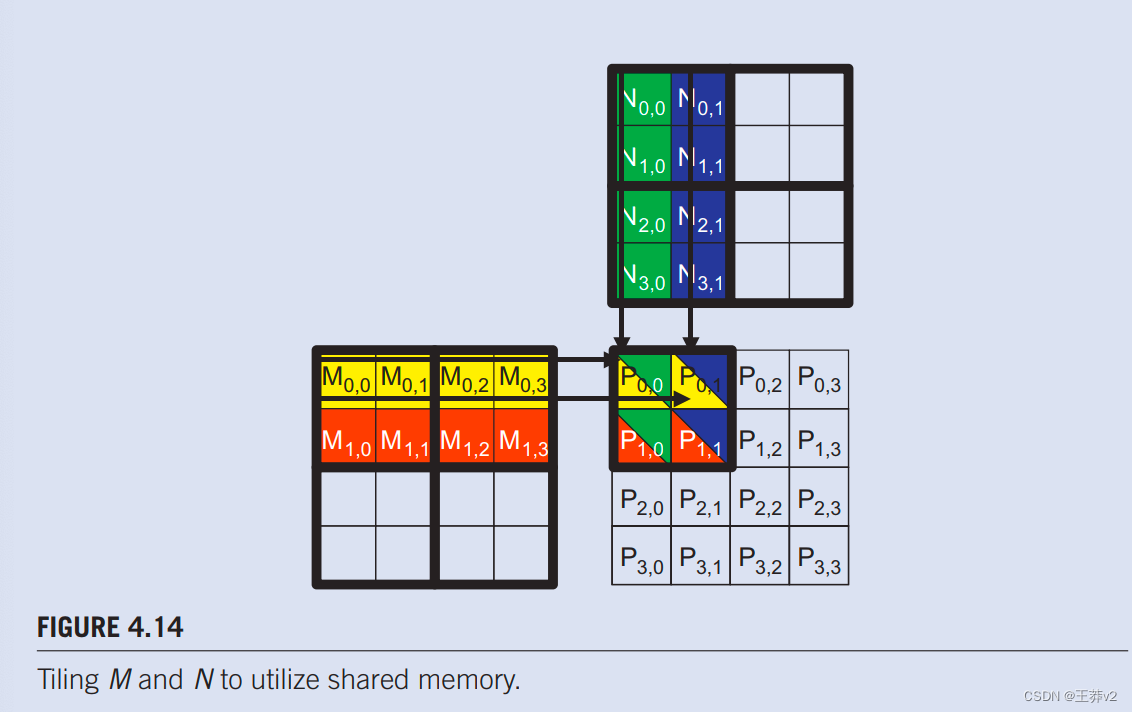
在图4.14中，我们将M和N分成2 x 2的tile，由粗线划定。每个线程执行的点积计算现在分为几个阶段。在每个阶段，一个块中的所有线程都协作，将M的tile和N的tile加载到共享内存中。这种协作可以通过将块中的每个线程加载一个M元素和一个N元素加载到共享内存中来实现，如图所示。4.15.图中的每一行。4.15显示线程的执行活动。请注意，时间从左到右。我们只需要在block0.0中显示线程的活动：所有其他块都具有相同的行为。M元素的共享内存数组称为Mds，N元素的共享内存数组称为Nds。在第1阶段开始时，block0.0的四个线程协同将M的tile加载到共享内存中：threde0.0将M0.0加载到MdS0，0，thread0.1加载M0.1到Mds0.1，thread1.o加载M1，o加载到Mds1.0，thread1，1将M1.1加载到Mds1，1，如图4.15中第二列所示。.N的tile也同样加载，如图4.15.中的第三列所示。

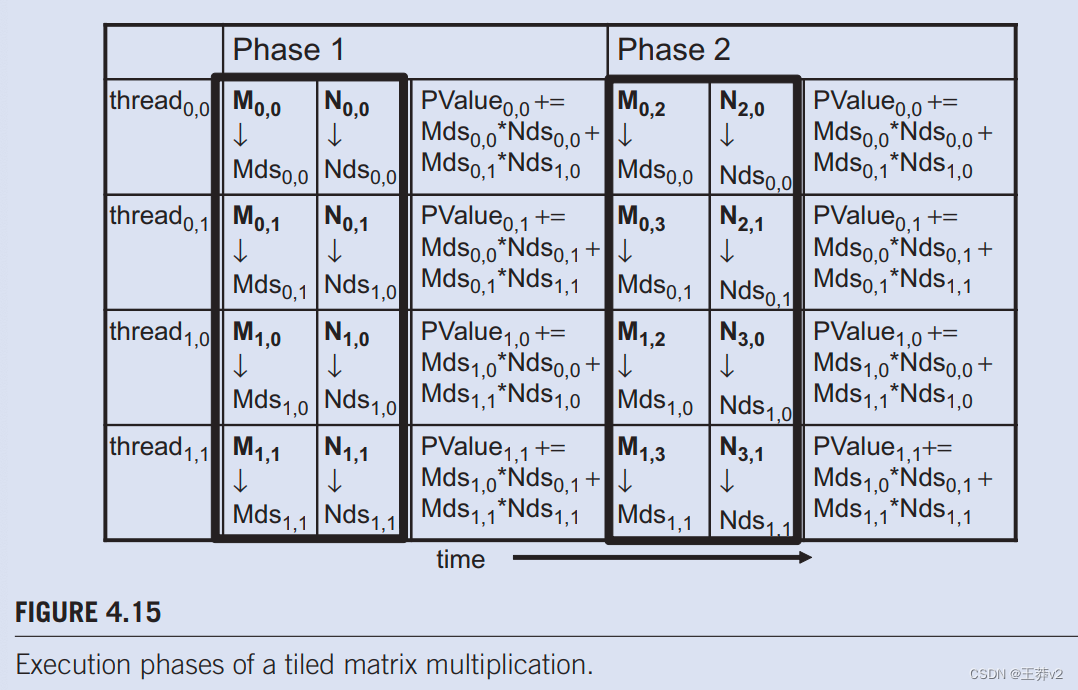
在将M和N的两个tile加载到共享内存中后，这些元素将用于计算点积。共享内存中的每个值被使用两次；例如，由 thread1.1 加载到 Mds1.1的 M1.1值被使用两次：第一次由 thread1.0使用，第二次由 threadi1.1使用。通过将每个gobal内存值加载到共享内存中，使其可以多次使用，我们减少了对全局内存的访问次数；在这种情况下，我们将其减少一半。读者应验证，如果tile是N x N元素，则减少的发生率为N倍。

请注意，图4.3中每个点积的计算。现在分两个阶段执行，图4.15中的阶段1和2。.在每个阶段，两对输入矩阵元素的乘积累积到Pvalue变量中。Pvalue是一个自动变量；为每个线程生成一个私有版本。我们添加了下标，以指示为每个线程创建的Pvalue变量的不同实例。第一阶段和第二阶段的计算显示在图4.15中的第四和第七列中。一般来说，如果输入矩阵的维度为Width，并且tile大小称为TILE_WIDTH，则点积将在Width/TILE_WIDTH阶段执行。创建这些阶段是减少对全局内存访问的关键。随着每个阶段专注于输入矩阵值的小子集，线程可以协作将子集加载到共享内存中，并使用共享内存中的值来满足该阶段中重叠的输入需求。

另请注意，Mds和Nds被重复使用来保存输入值。在每个阶段，相同的Mds和Nds用于在相位中保存M和N元素的子集，从而允许更小的共享内存为global内存的大部分访问提供服务。这是因为每个阶段都集中在输入矩阵元素的一小部分。这种集中的访问行为被称为局部性。当算法显示局部性时，就有机会使用小型高速存储器，以便为大多数访问提供服务，并从全局存储器中删除这些访问。本地性对于在多核CPU中实现高性能与在多线程GPU中一样重要。我们将回到第5章“性能考虑”中的地方性概念。