刷题的第二十八天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day28 任务
● 343. 整数拆分
● 96.不同的二叉搜索树

1 整数拆分

343. 整数拆分

思路：
动态规划
（1）确定dp数组（dp table）以及下标的含义
dp[i]：分拆数字i，可以得到的最大乘积为dp[i]
（2）确定递推公式

从1遍历j，然后有两种渠道得到dp[i]：（1）j * (i - j) 直接相乘（2）j * dp[i - j]，相当于是拆分(i - j)
$dp[i]=max(dp[i],max((i-j)\ast j,dp[i-j]\ast j));$

（3）dp的初始化

dp[2] = 1;

（4）确定遍历顺序

dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历

for (int i = 3; i <= n; i++) {
	for (int j = 1; j < i - 1; j++) {
		dp[i] = max(dp[i], max(dp[i - j] * j, (i - j) * j));
	}
}

优化：

for (int i = 3; i <= n; i++) {
	for (int j = 1; j <= i / 2; j++) {
		dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
	}
}

拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的
（5）举例推导dp数组

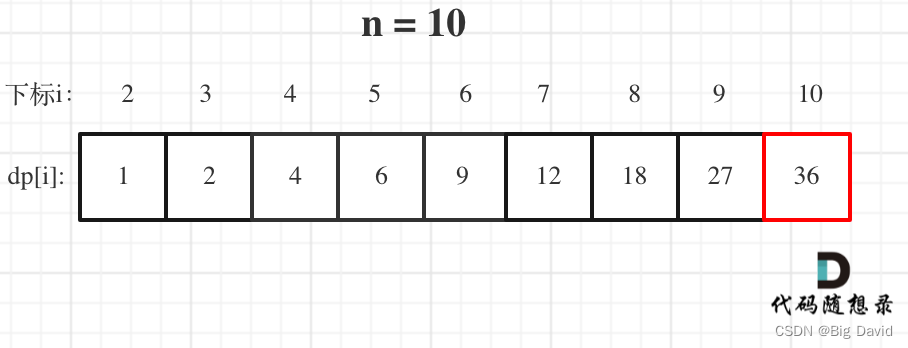
C++：

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j < i - 1; j++) {
                dp[i] = max(dp[i], max(dp[i - j] * j, (i - j) * j));
            }
        }
        return dp[n];
    }
};

时间复杂度：$O(n^2)$
空间复杂度：$O(n)$
优化之后：

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], max(dp[i - j] * j, (i - j) * j));
            }
        }
        return dp[n];
    }
};

2 不同的二叉搜索树

96.不同的二叉搜索树

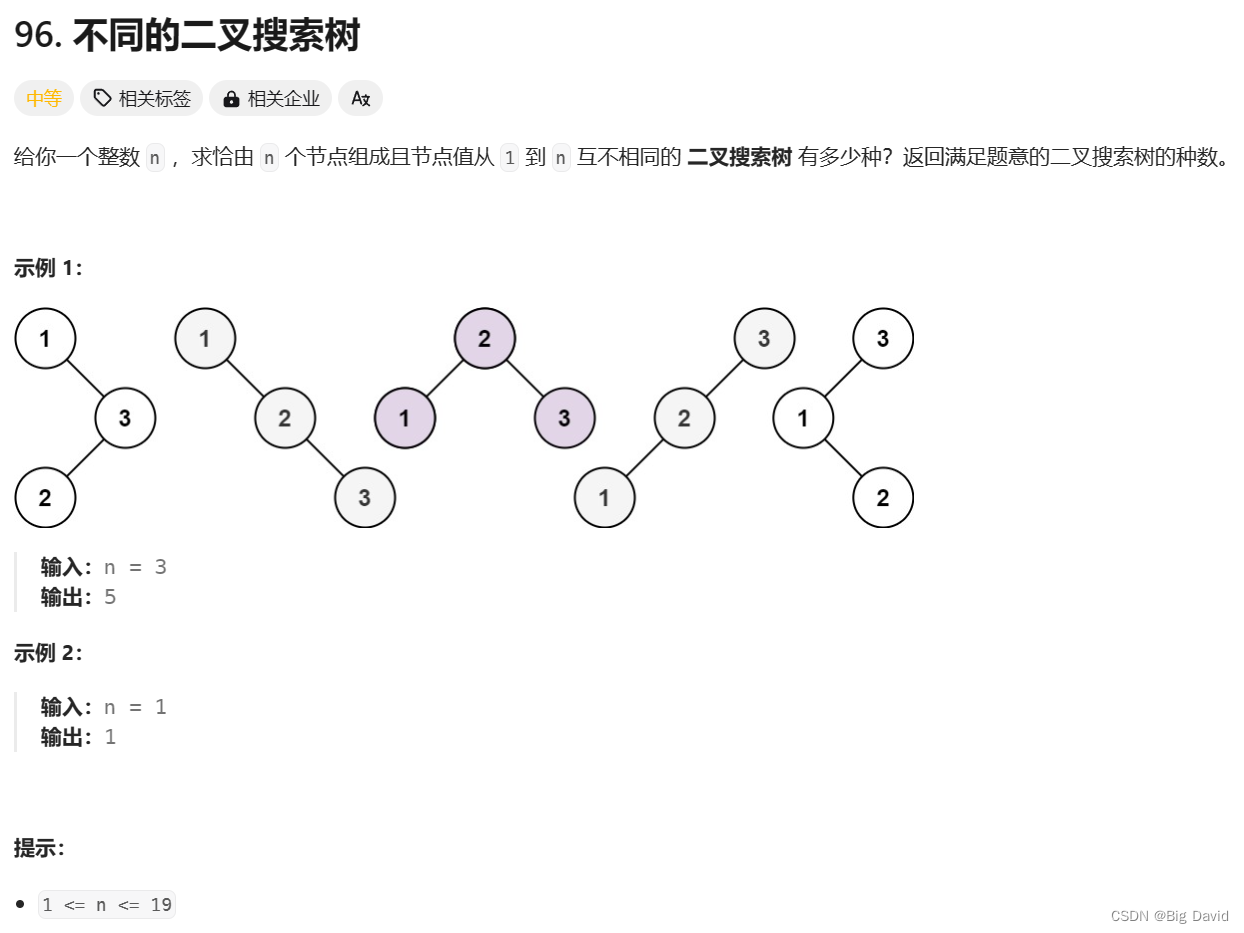
思路：
动态规划

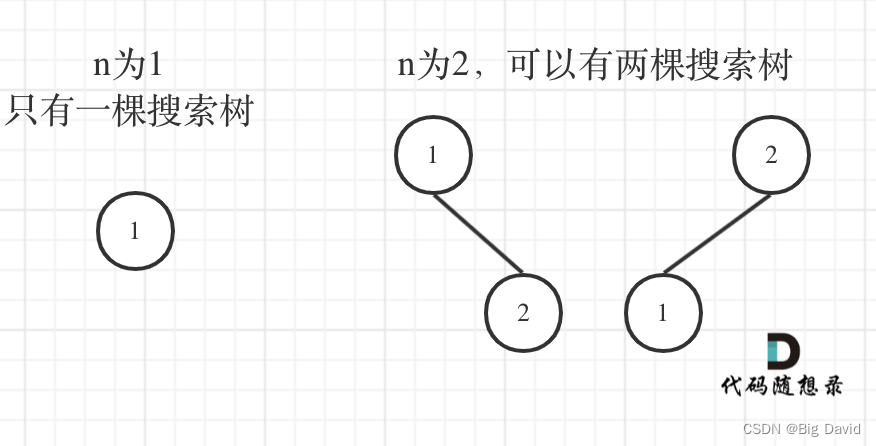
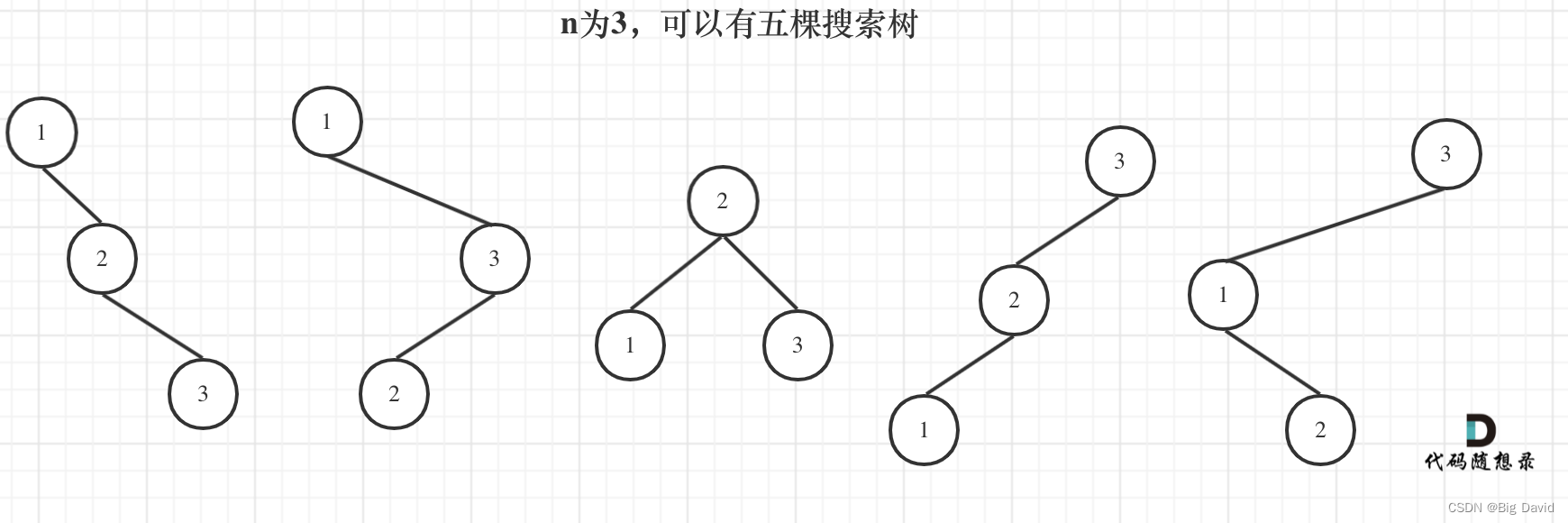
dp[3]，就是元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
（1）元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
（2）元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
（3）元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

$dp[3]=dp[2]\ast dp[0]+dp[1]\ast dp[1]+dp[0]\ast dp[2]$

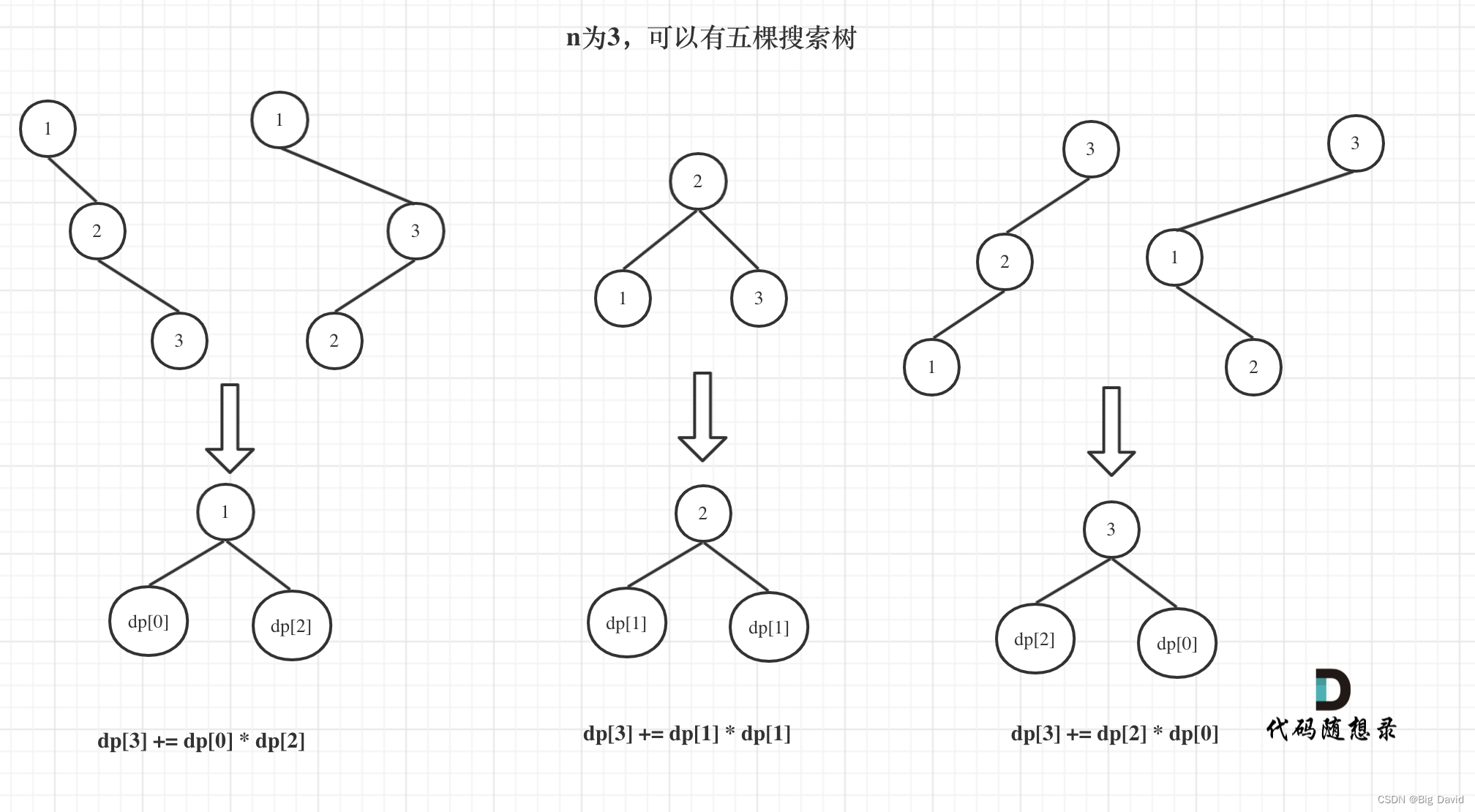
（1）确定dp数组以及下标的含义

dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]

（2）确定递推公式

dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]

dp[i] += dp[j - 1] * dp[i - j]; j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

（3）dp数组如何初始化：dp[0] = 1
（4）确定遍历顺序

for (int i = 1; i <= n; i++) {
	for (int j = 1; j <= i; j++) {
		dp[i] += dp[j - 1] * dp[i - j];
	}
}

（5）举例推导dp数组

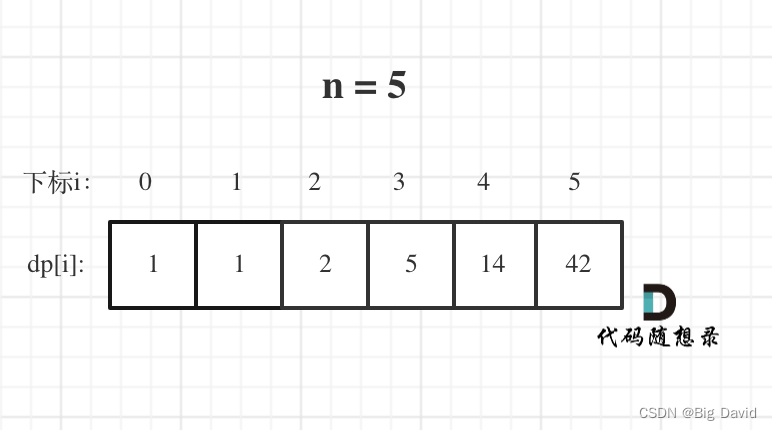
C++：

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[i - j] * dp[j - 1];
            }
        }
        return dp[n];
    }
};

时间复杂度：$O(n^2)$
空间复杂度：$O(n)$

---

鼓励坚持二十九天的自己😀😀😀