点名

点名

某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席，请返回他的学号。

二分法思路：判断数组的值和对应的下标是否相等，将数组分为两个区间，不相等区间的最左端，就是第缺席的同学的学号。 

class Solution {
public:
    int takeAttendance(vector<int>& records) {
        int left = 0, right = records.size() - 1;
        while(left < right)
        {
            // 判断数组的值和下标是否相等，可以将其分为两个区间
            int mid = left + (right - left)/2;
            if(records[mid]!=mid)  right= mid;
            else if(records[mid]==mid) left = mid + 1;
        }
        if(left == records[records.size()-1]) return left+1;
        else return left;
    }
};

山脉数组的峰顶索引 

山脉数组的峰顶索引

符合下列属性的数组 arr 称为 山脉数组 ：

• arr.length >= 3
• 存在 i（0 < i < arr.length - 1）使得：
  • arr[0] < arr[1] < ... arr[i-1] < arr[i]
  • arr[i] > arr[i+1] > ... > arr[arr.length - 1]

给你由整数组成的山脉数组 arr ，返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。

你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。

 

按照题目要求，数组一定存在先递增，再递减的情况。根据这个特性，可以将数组分为两个区间，一个为递增区间（包含顶峰），一个是递减区间，不包含顶峰，根据这个二项性来使用二分算法解决！

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
        //这个数组具有二段性 --> 可以采用二分查找
        int left = 0, right = arr.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left + 1)/2;
            //一段为山峰向上，包括山峰
            if(arr[mid] < arr[mid-1]) right = mid - 1;
            else left = mid; 
        }
        return left;
    }
};

寻找峰值 

 寻找峰值

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

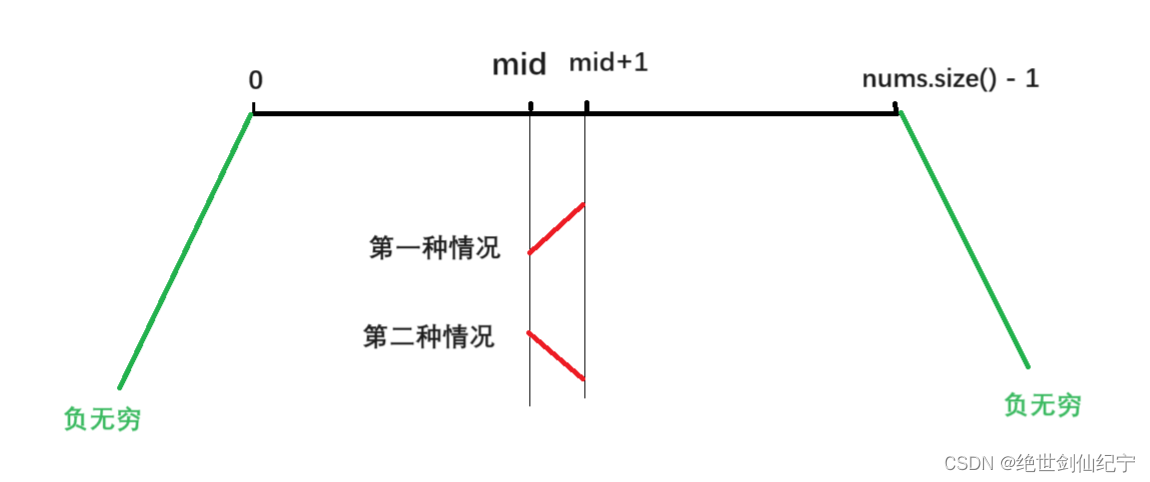
思路，因为数组外面的值都是负无穷，所以数组依然有 “二段性” ，当 nums[mid] > nums[mid+1] 的时候，并且由于数组最左边是负无穷，所以在左半区间一定存在一个“峰值”，则舍去右区间；同理当 nums[mid] < nums[mid+1] 时，可舍去左区间。利用这个二段性，使用二分法求解！

 

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        //数组依然有二段性
        int left = 0, right = nums.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left)/2;
            // 左区间有结果
            if(nums[mid] > nums[mid+1]) right = mid;
            //右区间有结果
            else if(nums[mid] < nums[mid+1]) left = mid + 1; 
        }
        return left;
    }
};

寻找旋转排序数组中的最小值 

寻找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

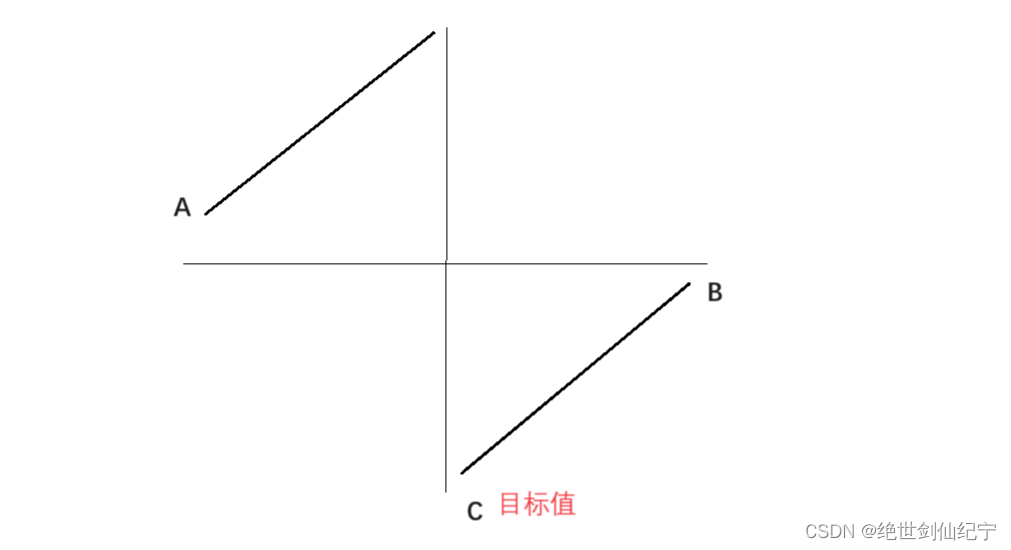
思路：以B点或者A点作为边界条件，大于等于A或者大于B分为一组，小于A或者小于等于B分为一组，使用二分法逐渐舍去另一组不符合的，最终的left位置就是 最小元素 的位置。（注：如果使用A 点为边界点，需要注意边界条件：A点为最小值）

 

class Solution {
public:
    int findMin(vector<int>& nums) {
        // 有二段性:两段区间都是递增的
        // 采用二分查找，且以左区间的第一个数为分界
        int left = 0, right = nums.size() - 1;
        if(nums[left]<nums[right]) return nums[left];
        while(left < right)
        {
            int mid = left + (right - left)/2;
            if(nums[mid] >= nums[0]) left = mid + 1;
            else if(nums[mid] < nums[0]) right = mid;
        }
        return nums[left];
    }
};