---

本系列文章介绍强化学习基础知识与经典算法原理，大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程（参考资料1），并参考了部分参考资料2、3的内容进行补充。

系列博文索引：

• 强化学习的数学原理学习笔记 - RL基础知识
• 强化学习的数学原理学习笔记 - 基于模型（Model-based）
• 强化学习的数学原理学习笔记 - 蒙特卡洛方法（Monte Carlo）
• 强化学习的数学原理学习笔记 - 时序差分学习（Temporal Difference）
• 强化学习的数学原理学习笔记 - 值函数近似（Value Function Approximation）
• 强化学习的数学原理学习笔记 - 策略梯度（Policy Gradient）
• 强化学习的数学原理学习笔记 - Actor-Critic

参考资料：

1. 【强化学习的数学原理】课程：从零开始到透彻理解（完结）（主要）
2. Sutton & Barto Book: Reinforcement Learning: An Introduction
3. 机器学习笔记

*注：【】内文字为个人想法，不一定准确

概览：RL方法分类

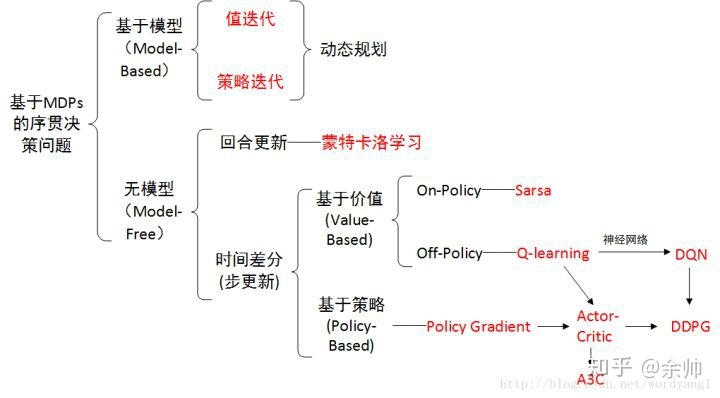
*图源：https://zhuanlan.zhihu.com/p/36494307

RL算法中存在两种策略：

• 行为策略（Behavior policy）：与环境交互，生成experience采样
• 目标策略（Target policy）：迭代更新，直到收敛至最优策略

据此，可以将RL算法分为两类：

• On-policy：Behavior policy即为Target policy，例如MC、Sarsa等
• Off-policy：Behavior policy与Target policy可以不同，例如Q-learning等
  • 好处：从别的策略得到的经验中学习，允许更为广泛的探索而不必考虑利用

*On-policy可以看作是Off-policy的一种特殊情况，因为Off-policy允许两种策略相同。

基于模型（Model-Based）

基于模型：环境MDP的模型已知，基于动态规划（DP）求解

• 优：提供了RL的理论基础
• 劣：假设过强（完美的环境模型，比如状态转移矩阵），计算开销过高

基于模型的方法：

• 策略迭代：收敛速度较快，适用于小状态空间
• 值迭代：计算量较少，适用于大状态空间

*值迭代可以看作是策略迭代的一种特殊情况

值迭代（Value Iteration）

算法步骤：在第$k$次迭代中

• 策略更新：给定$v_k$，求解对应的策略${\pi }_{k+1}={\mathrm{argmax}}_{\pi }(r_{\pi }+\gamma P_{\pi }{v}_k)$
• 值更新：根据策略${\pi }_{k+1}$，计算$v_{k+1}=r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}+v_k$
  • *此处的$v_k$并非状态值，只是一个值，因为其并不满足贝尔曼方程

*详细步骤见强化学习的数学原理学习笔记 - 基础知识中求解贝尔曼最优方程部分。

算法公式：
$$v_{k+1}(s)=\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })]$$

伪代码：

v[0] = init_state_value()

while ||v_[k] - v_[k-1]|| >= threshold:
    for s in StateSpace:
        for a in ActionSpace:
            q[a] = calculate_q_value(s, a, v_[k])
    
    	a_star = get_optimal_action(q)

        # policy update
        pi[k+1] = update_policy(a_star)

        # value update
        v[k+1] = update_value(pi[k+1], v_[k])

    k = k + 1

值迭代可以看作将贝尔曼优化方程转为一个更新规则：先计算最优值函数，再从中提取对应的策略作为最优策略

🟦策略迭代（Policy Iteration）

反复执行策略评估（Policy Evaluation，PE）和策略提升（Policy Improvement，PI），直至收敛至最优策略。【*能够收敛的要求：有限MDP仅有有限个策略】

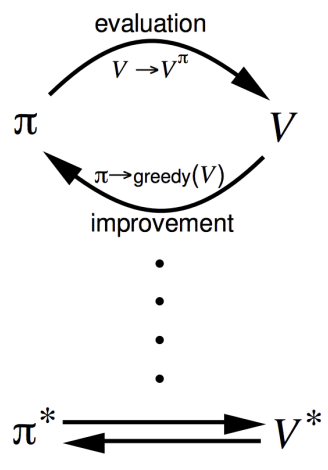
• 策略评估：评价某个策略本身如何，即计算任意策略$\pi$的状态值函数$v_{\pi }$，称之为预测问题（Prediction Problem ）
  • $v_{k+1}(s)={\sum }_a\pi (a|s){\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })]$
    • 注意这里与值迭代的区别：值迭代直接求解最优的状态值，而策略评估仅是计算当前策略的状态值（并不一定是最优）
• 策略提升：寻找每个状态下的最好的动作
  • 考虑在状态$s$下找到了一个优于现有策略$\pi$的动作$a={\pi }^{\prime }(s)\ne \pi (s)$，则对应的动作值函数$q_{\pi }(s,a)$不低于状态值函数$v_{\pi }(s)$，即：$q_{\pi }(s,{\pi }^{\prime }(s))\ge v_{\pi }(s)$
  • 新策略${\pi }^{\prime }$不差于现有策略$\pi$，即满足：$v_{{\pi }^{\prime }}(s)\ge v_{\pi }(s)$
  • 那么策略提升就是以贪心的方式选择每个状态下能使动作值函数最大的动作，进而更新策略：${\pi }^{\prime }(s)={\mathrm{argmax}}_a{q}_{\pi }(s,a)={\mathrm{argmax}}_a{\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]$

算法步骤：在第$k$次迭代中，给定策略${\pi }_k$（随机初始策略：${\pi }_0$）

• 策略评估：计算${\pi }_k$的状态值$v_{{\pi }_k}=r_{{\pi }_k}+\gamma P_{{\pi }_k}{v}_{{\pi }_k}$
  • *迭代中嵌套迭代，求解每次迭代策略的迭代状态值
• 策略提升：根据${\pi }_k$的状态值$v_{{\pi }_k}$，求解当前的最优策略${\pi }_{k+1}$

伪代码：

pi[0] = init_policy()

while not pi[k].is_converged:
    # policy evaluation
    while ||v_[j] - v_[j-1]|| >= threshold:
        for s in StateSpace:
            v_[j+1][s] = calculate_state_value(pi[k], v_[j][s])
        j = j + 1

    # policy improvement
    for s in StateSpace:
        for a in ActionSpace:
            q[a] = calculate_q_value(s, a, v[j])
    
    	a_star = get_optimal_action(q)
        pi[k+1] = update_policy(a_star)

	k = k + 1

*策略迭代中，距离最终目标状态（考虑一个episode的最终状态）越近的状态的策略会越早收敛，离目标状态越远的状态的策略会越晚收敛

🟡截断策略迭代（Truncated Policy Iteration）

截断策略迭代是值迭代与策略迭代的一般化推广；反过来讲，值迭代与策略迭代都是截断策略迭代的特殊情况。

值迭代 vs. 策略迭代：

• 令$v_0=v_{{\pi }_0}$，使得二者具有相同的初始值，便于比较
• 发现：二者的区别在于第四步的$v_{{\pi }_1}\ne v_1$，因此后续的所有迭代中，二者结果均不相同（收敛前）
  • $v_{{\pi }_1}$是由贝尔曼最优方程计算出的状态值，而$v_1$只是一个值（不是状态值）

可以发现，值迭代与策略迭代的根本差异，在于基于贝尔曼最优公式求解状态值的过程

• 值迭代：仅基于初始状态值，求解一次贝尔曼最优公式
• 策略迭代：在策略评估部分，每次迭代求解贝尔曼公式（∞次）
  • *实际中，当两次迭代的状态值差异不大的时候，可以认为已经收敛了

而截断策略迭代就是更一般化的情况：迭代$j$次计算状态值，其中$1\le j<\infty$

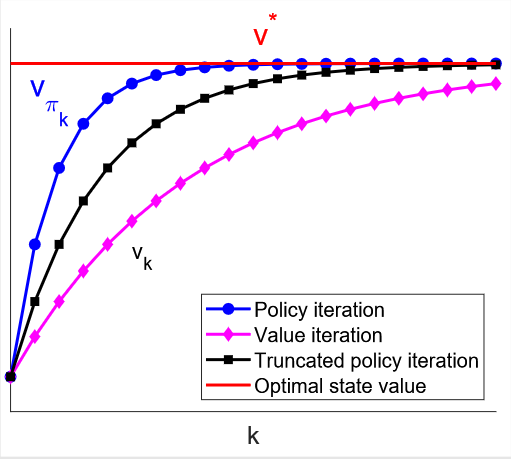
注：实际上，策略评估与策略提升是一种非常通用的强化学习思想（称为通用策略迭代，GPI），并在许多后续的强化学习方法（如蒙特卡洛方法、时序差分学习等）中有着广泛应用。