文章目录
- 💖 [学习资源整合](https://www.cnblogs.com/duisheng/p/17872980.html)
- 📚 总复习
- 📕 知识点
- ⭐ 常用分布的数学期望和方差
- 📙 选择题
- 📙 填空题
- 📙 大题
- 1. 概率
- 2. 概率
- 3. 概率
- 4. P
- 5. 概率
- 6. 概率密度函数 F ( X ) F(X) F(X)
- 7. 分布列求方差 V ( X ) V(X) V(X)
- 8. 求分布函数 F ( X ) F(X) F(X)
- 9. 求 F ( X ) F(X) F(X) 和 P ( X ) P(X) P(X)
- 10. 求未知数 k k k, F ( X ) F(X) F(X), P ( X ) P(X) P(X)
- 11. 分布列
- 12. 知 E ( X ) E(X) E(X) 求 f ( x ) f(x) f(x) 中的未知数
- 13. 概率密度 求 k , E ( X ) , P ( 0 < X < 1 2 ) k,E(X),P(0< X < \frac{1}{2}) k,E(X),P(0<X<21)
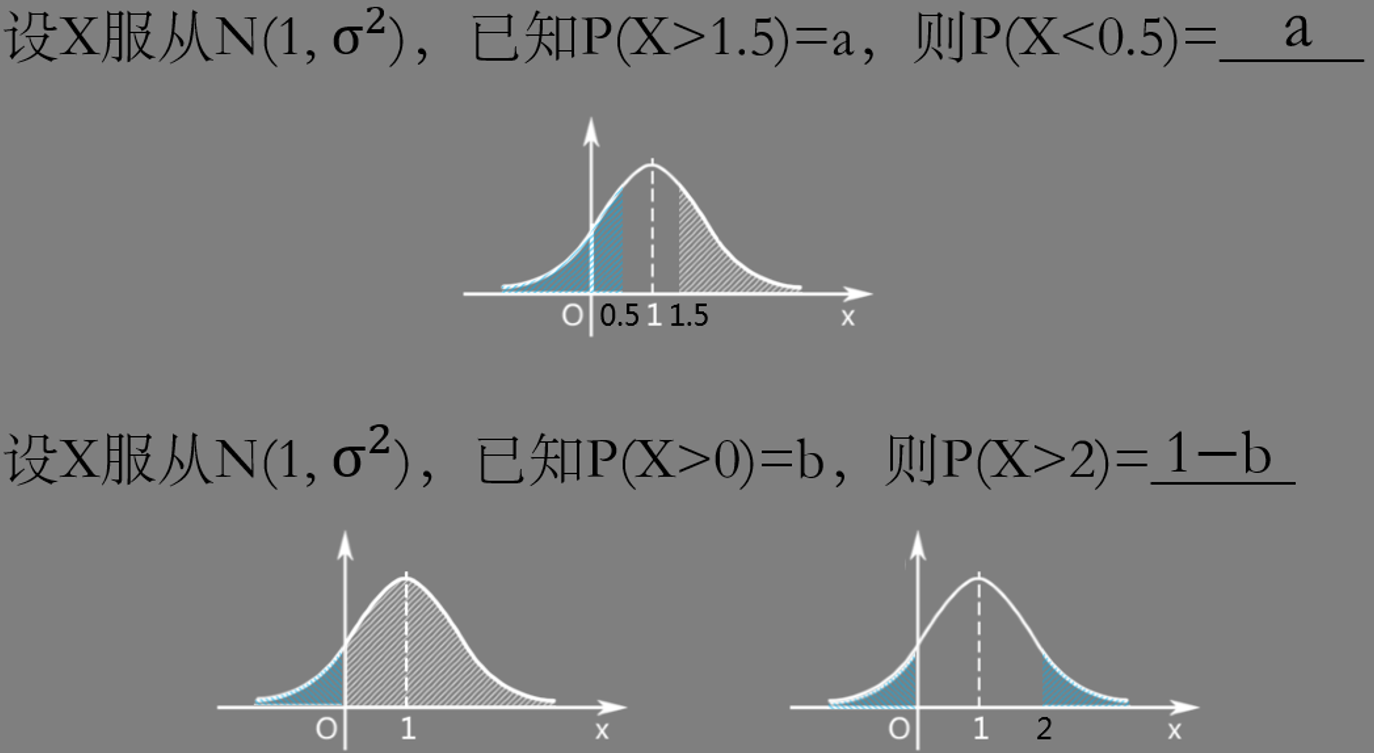
- 14. 正态分布求 P ( X > x ) ≤ 0.05 P(X>x)\le0.05 P(X>x)≤0.05 的最小 x x x
- 15. 正态分布求 P ( a < X < b ) P(a<X<b) P(a<X<b)
- 16. 正态分布求 P P P
- 💖 实验习题
- 💖 速成课
- 一、事件的概率
- 1. 无放回类题目
- 2. 有放回类的题目
- 3. 需要画图的题目
- 4. 条件概率
- 5. 全概率公式
- 6. 贝叶斯公式
- 二、一维随机变量
- 三、一维随机变量函数
- 四、五种常见的分布
- 1. 均匀分布
- 2. 泊松分布
- 3. 二项分布
- 4. 指数分布
- 5. 正态分布
- 6. 正态分布图像
- 五、二维随机变量
- 1. 二维离散型分布律求概率
- 2. 二维离散型分布律求独立性
- 3. 知 F ( x , y ) F(x,y) F(x,y) 求 f ( x , y ) f(x,y) f(x,y)
- 4. 知 f ( x , y ) f(x,y) f(x,y) 求 F ( x , y ) F(x,y) F(x,y)
- 5. 已知 F ( x , y ) F(x,y) F(x,y) 求 P P P
- 6. 已知 f ( x , y ) f(x,y) f(x,y) 求 P P P
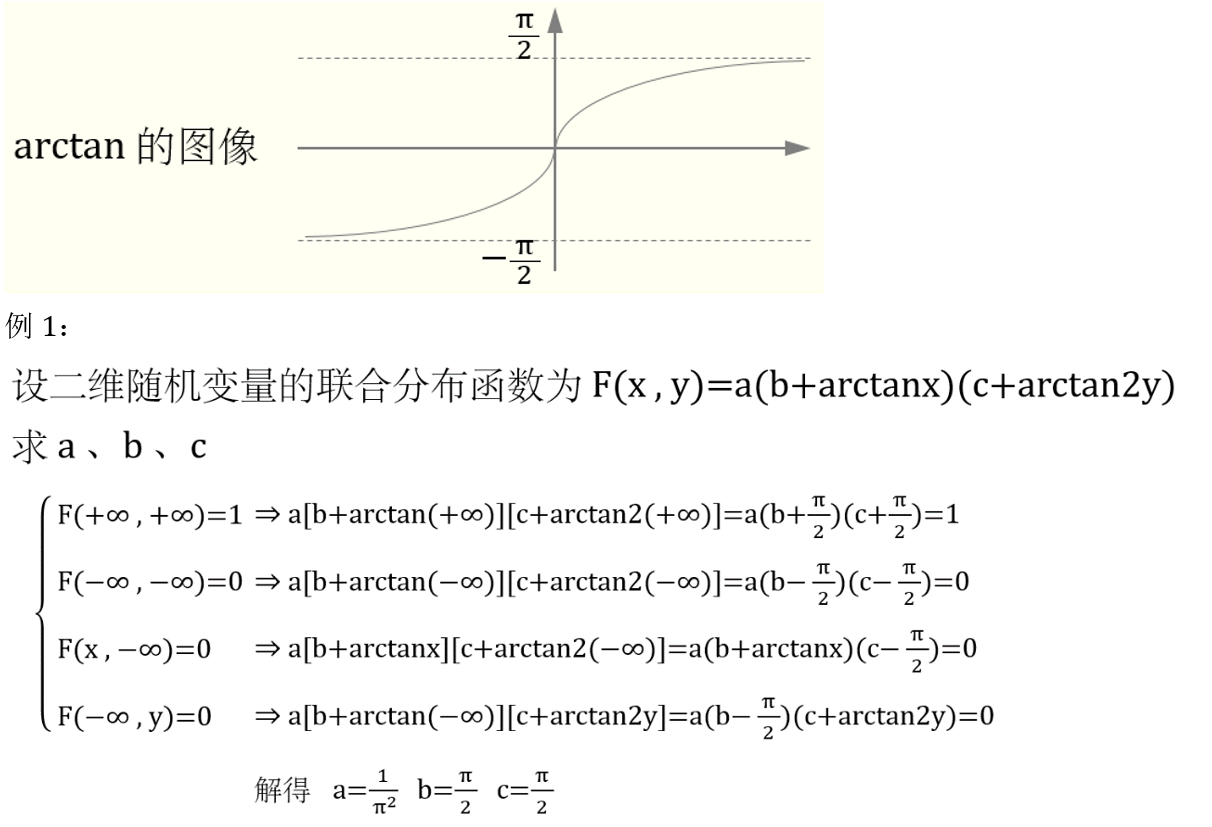
- 7. 已知 F ( x , y ) F(x,y) F(x,y) 或 f ( x , y ) f(x,y) f(x,y) 含有的未知数
- 8. 求均匀分布的 f ( x , y ) f(x,y) f(x,y) 与 P P P
- 六、期望与方差
- 七、中心极限定理
- 八、区间估计
- ⭐ 置信区间
- ⭐ 求置信区间
- 九、 假设检验
- ⭐ Z 检验
- ⭐ t 检验
- ⭐ x 2 x^2 x2 检验
💖 学习资源整合
📚 总复习
📕 知识点
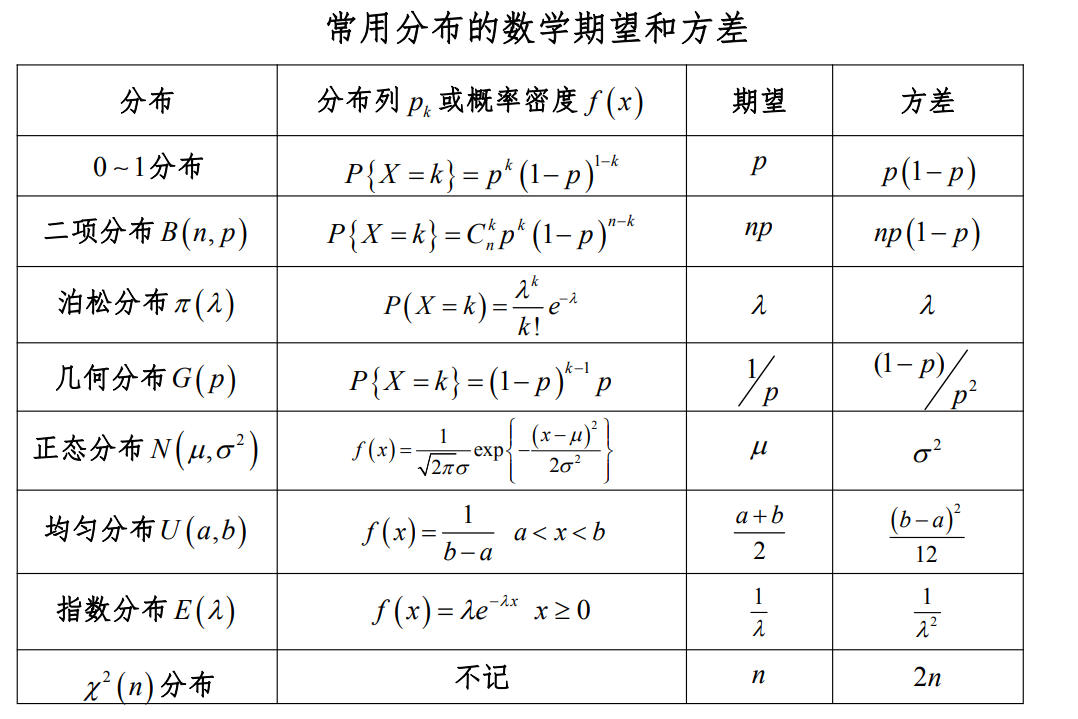
⭐ 常用分布的数学期望和方差
📙 选择题


📙 填空题


📙 大题
1. 概率

2. 概率

3. 概率

4. P

5. 概率

6. 概率密度函数 F ( X ) F(X) F(X)

7. 分布列求方差 V ( X ) V(X) V(X)

8. 求分布函数 F ( X ) F(X) F(X)
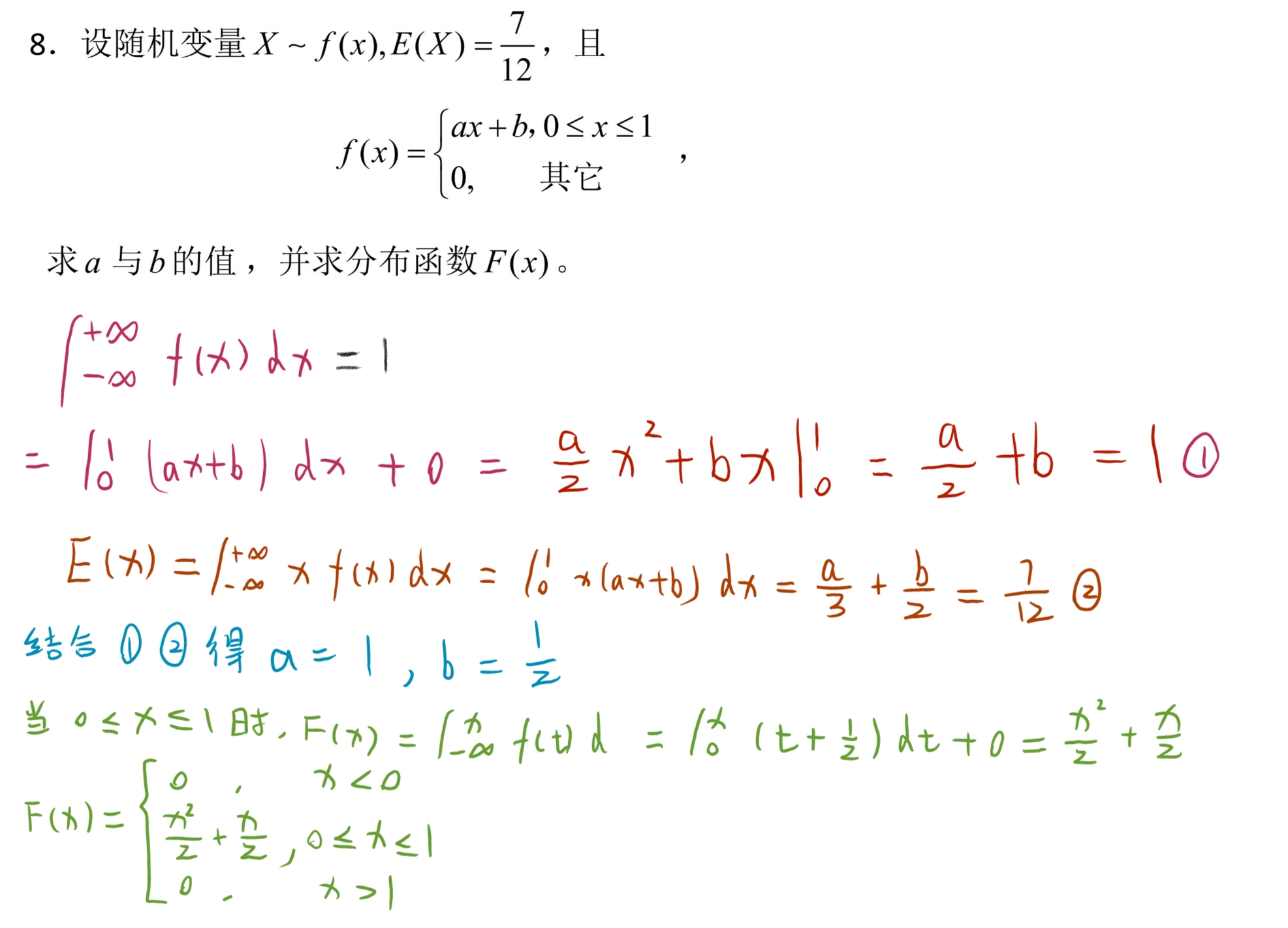
9. 求 F ( X ) F(X) F(X) 和 P ( X ) P(X) P(X)

10. 求未知数 k k k, F ( X ) F(X) F(X), P ( X ) P(X) P(X)

11. 分布列

12. 知 E ( X ) E(X) E(X) 求 f ( x ) f(x) f(x) 中的未知数

13. 概率密度 求 k , E ( X ) , P ( 0 < X < 1 2 ) k,E(X),P(0< X < \frac{1}{2}) k,E(X),P(0<X<21)

14. 正态分布求 P ( X > x ) ≤ 0.05 P(X>x)\le0.05 P(X>x)≤0.05 的最小 x x x

15. 正态分布求 P ( a < X < b ) P(a<X<b) P(a<X<b)

16. 正态分布求 P P P

💖 实验习题
💝 列联表资料的 x 2 x^2 x2 检验


💝 独立样本 T T T 检验
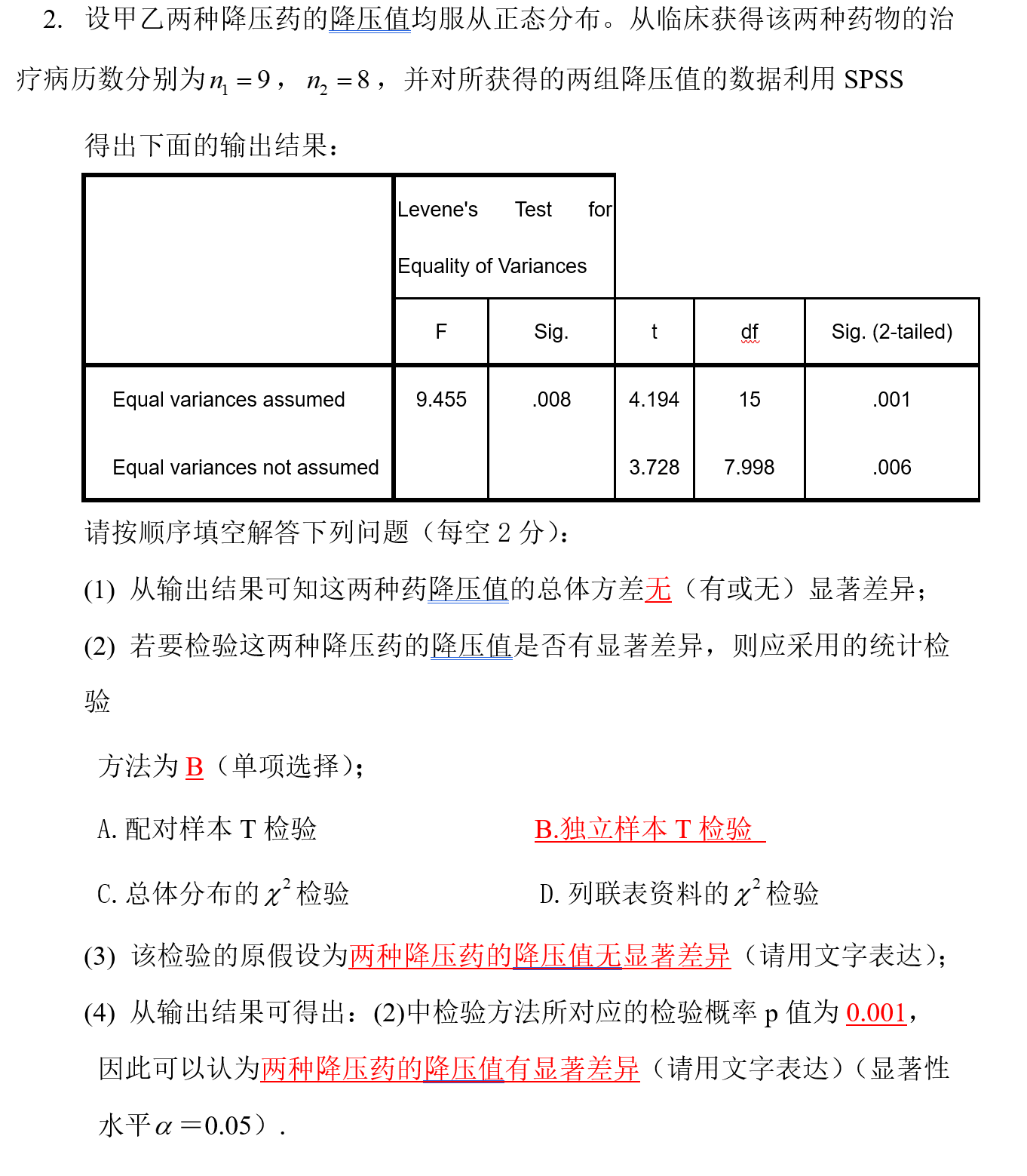
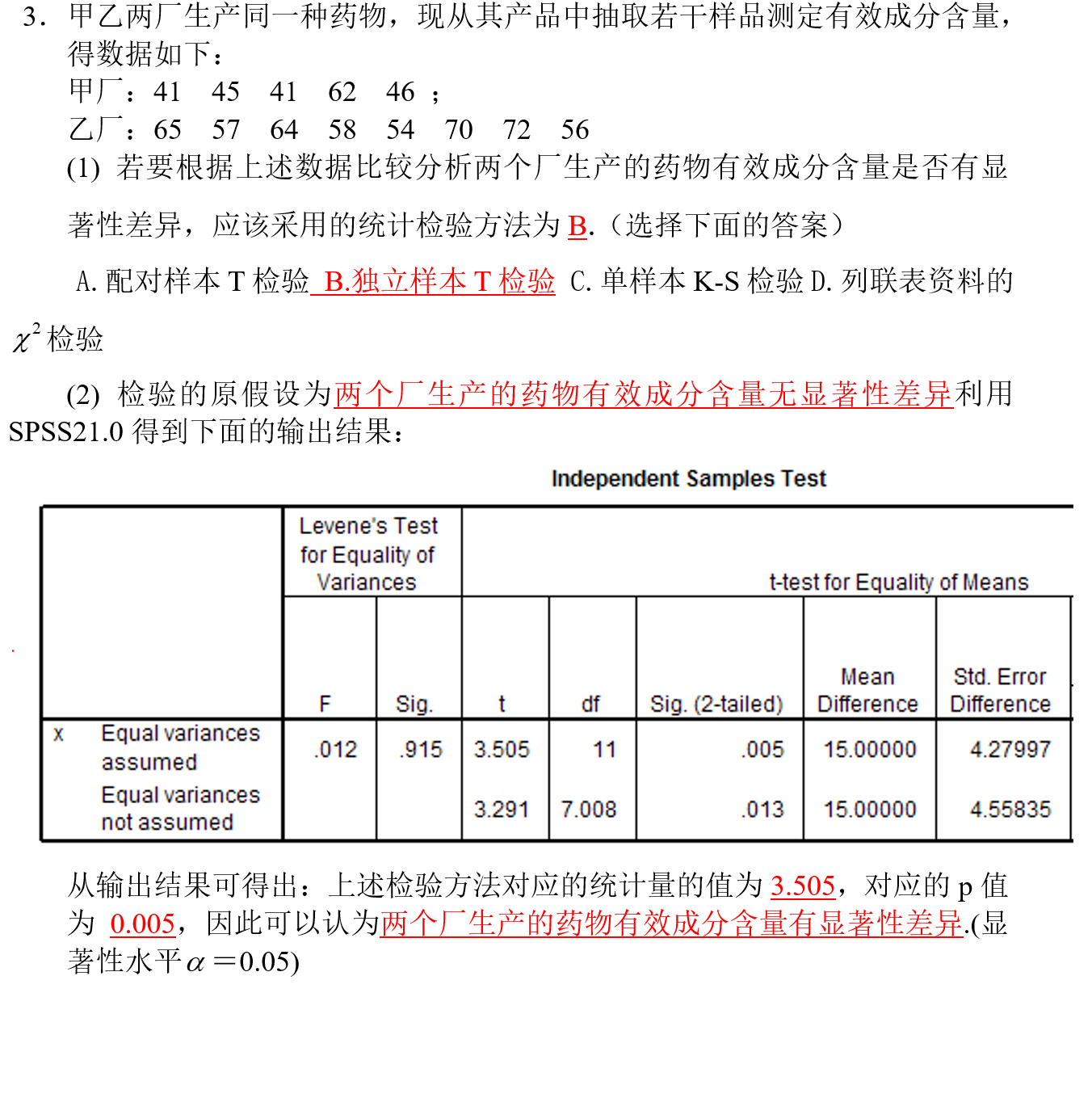
💝 配对样本 T T T 检验

💖 速成课
一、事件的概率
1. 无放回类题目



2. 有放回类的题目


3. 需要画图的题目
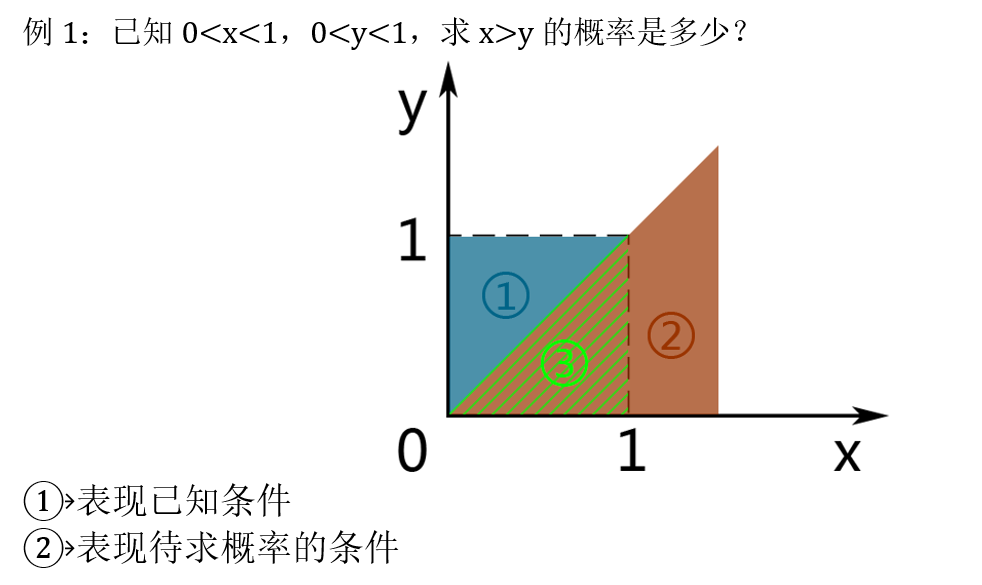
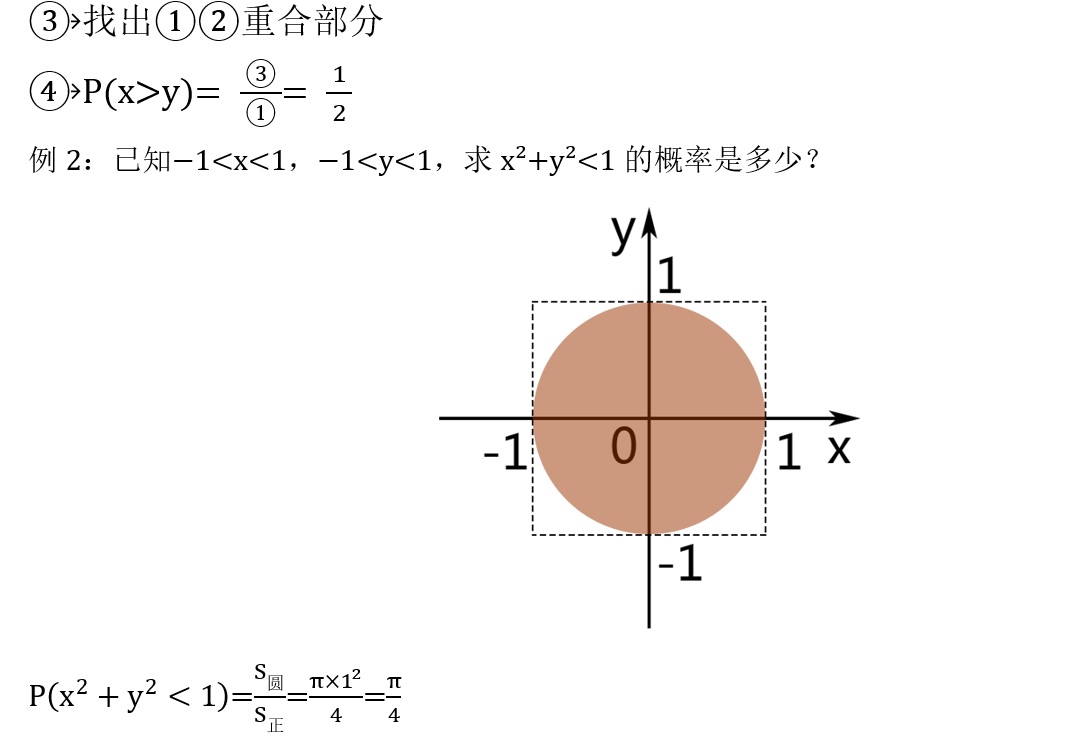

4. 条件概率




5. 全概率公式



6. 贝叶斯公式



二、一维随机变量
1. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 知一求二
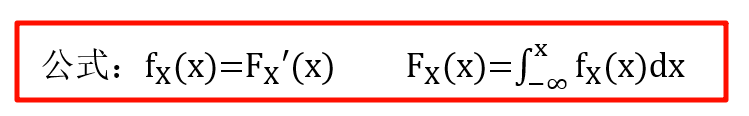
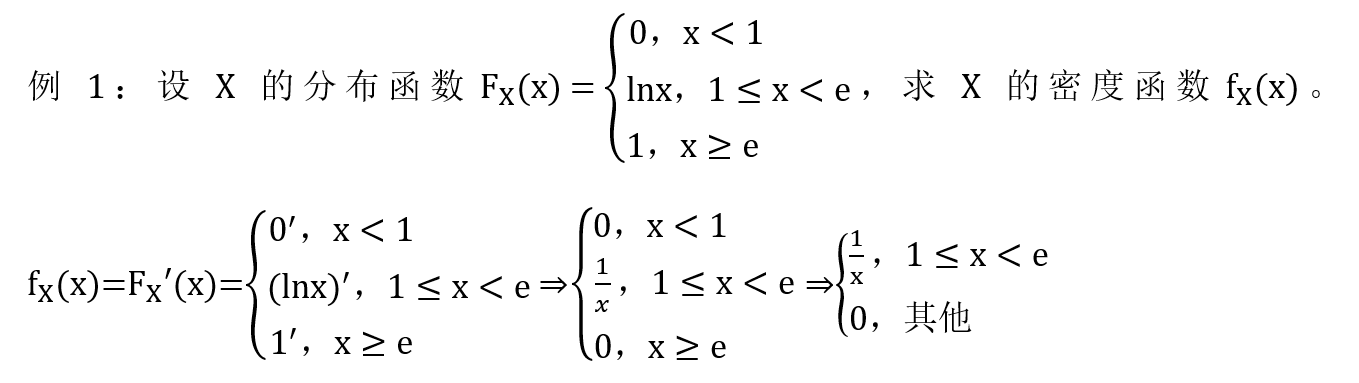

2. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 知一求 P P P
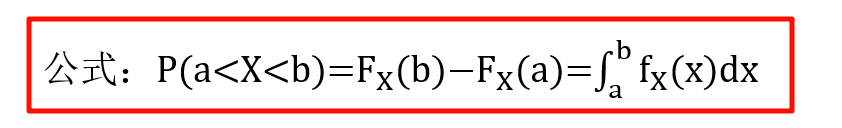
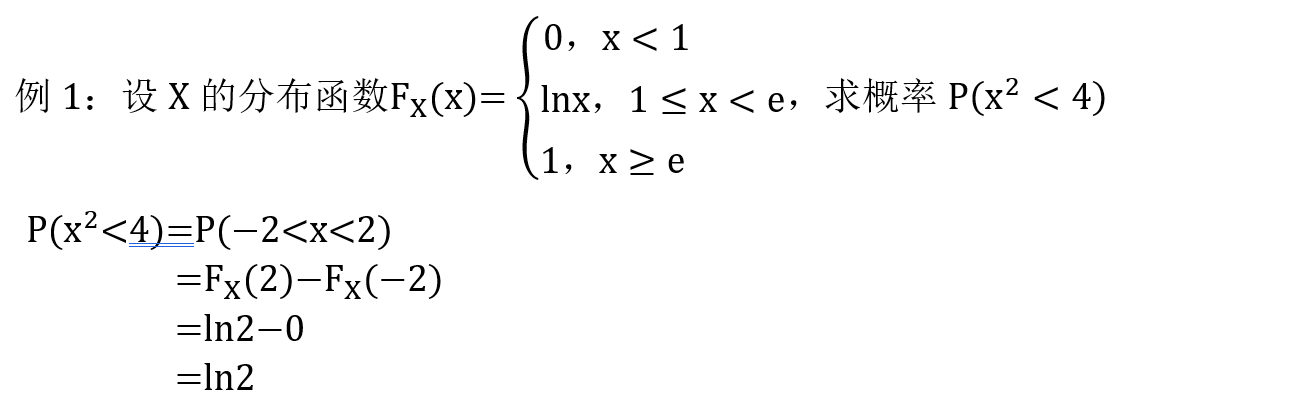

3. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 含未知数,求未知数
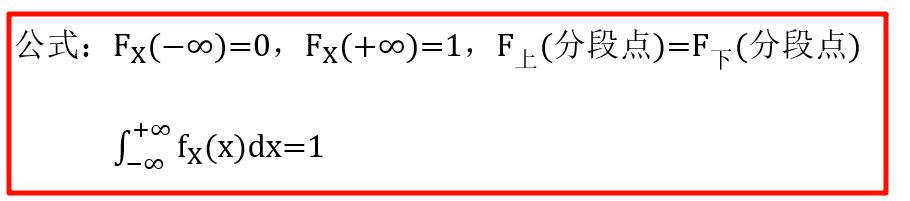


4. 求分布律

5. 已知含有未知数的分布列,求未知数

三、一维随机变量函数
1. 已知 X 分布列,求 Y 分布列


2. 已知 F X ( x ) F_X (x) FX(x),求 F Y ( y ) F_Y (y) FY(y)


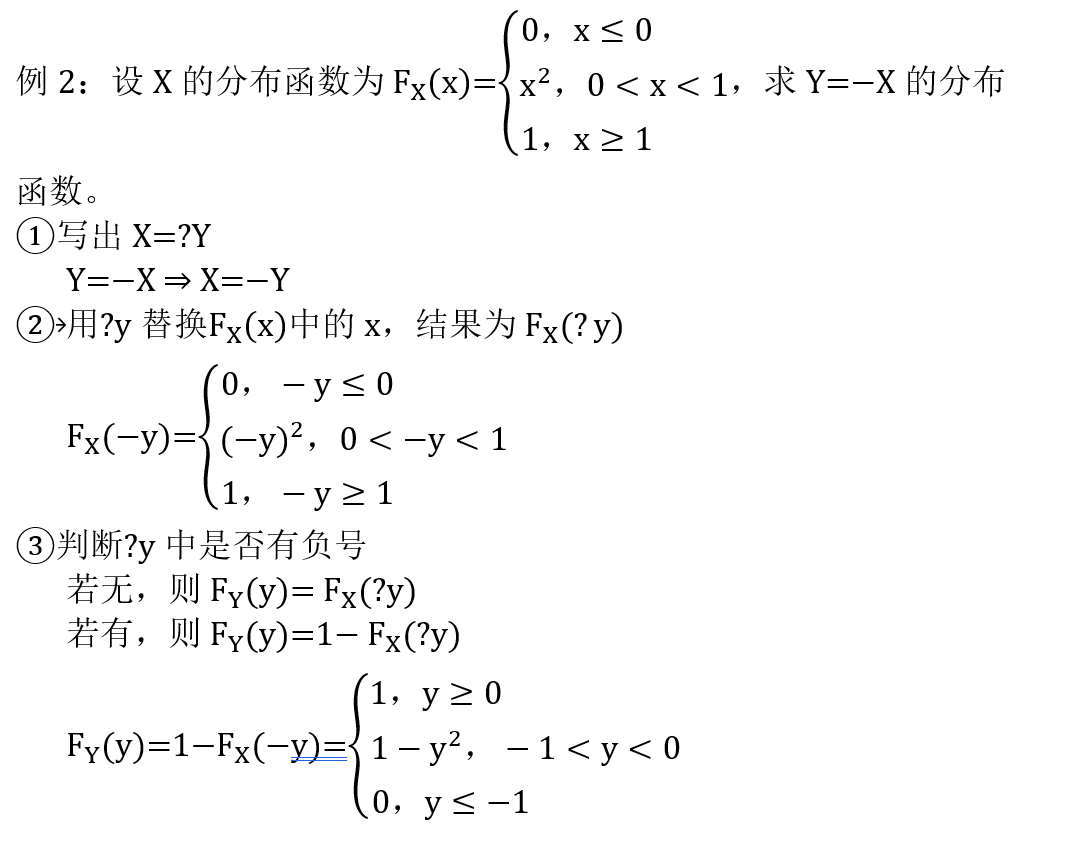
3. 已知 f X ( x ) f_X (x) fX(x),求 f Y ( y ) f_Y (y) fY(y)

四、五种常见的分布

1. 均匀分布



2. 泊松分布
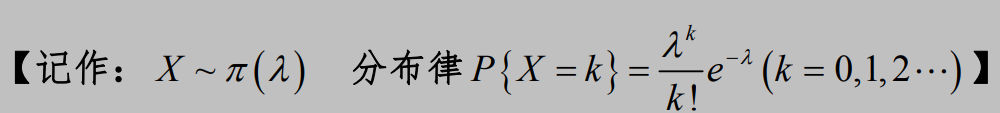
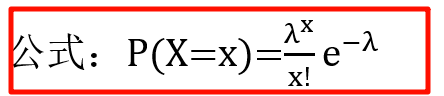

3. 二项分布




4. 指数分布



5. 正态分布



6. 正态分布图像


五、二维随机变量
1. 二维离散型分布律求概率


2. 二维离散型分布律求独立性



3. 知 F ( x , y ) F(x,y) F(x,y) 求 f ( x , y ) f(x,y) f(x,y)



4. 知 f ( x , y ) f(x,y) f(x,y) 求 F ( x , y ) F(x,y) F(x,y)






5. 已知 F ( x , y ) F(x,y) F(x,y) 求 P P P


6. 已知 f ( x , y ) f(x,y) f(x,y) 求 P P P


7. 已知 F ( x , y ) F(x,y) F(x,y) 或 f ( x , y ) f(x,y) f(x,y) 含有的未知数


8. 求均匀分布的 f ( x , y ) f(x,y) f(x,y) 与 P P P

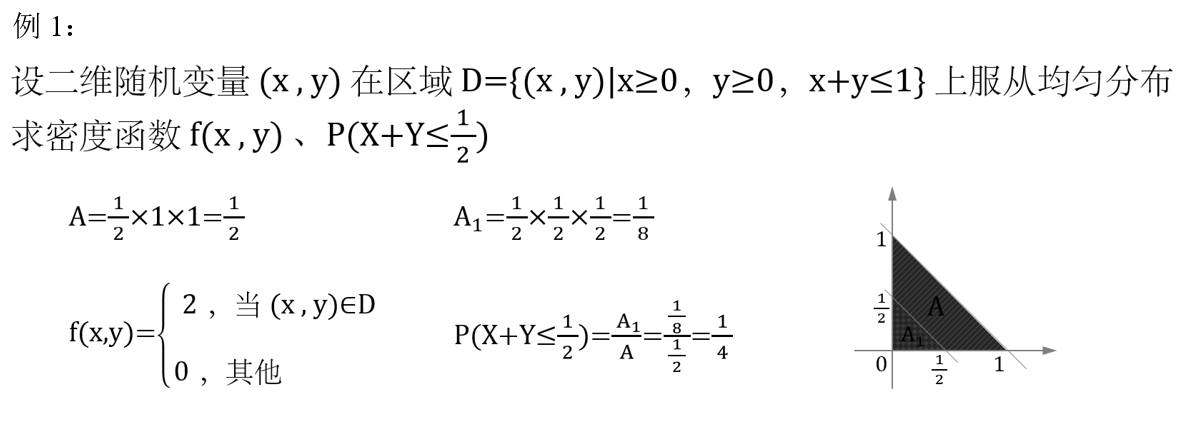
六、期望与方差
1. 离散型的期望 E ( x ) E(x) E(x)


2. 连续型的期望 E ( X ) E(X) E(X)


3. Y = g ( x ) Y=g(x) Y=g(x) 求 E ( Y ) E(Y) E(Y)



4. 方差 D ( X ) D(X) D(X)
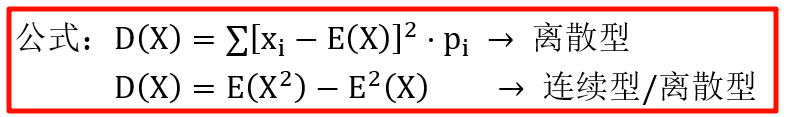
例1


5. 根据 E ( X ) 、 D ( X ) E(X)、D(X) E(X)、D(X) 的性质进行复杂运算 ⭐

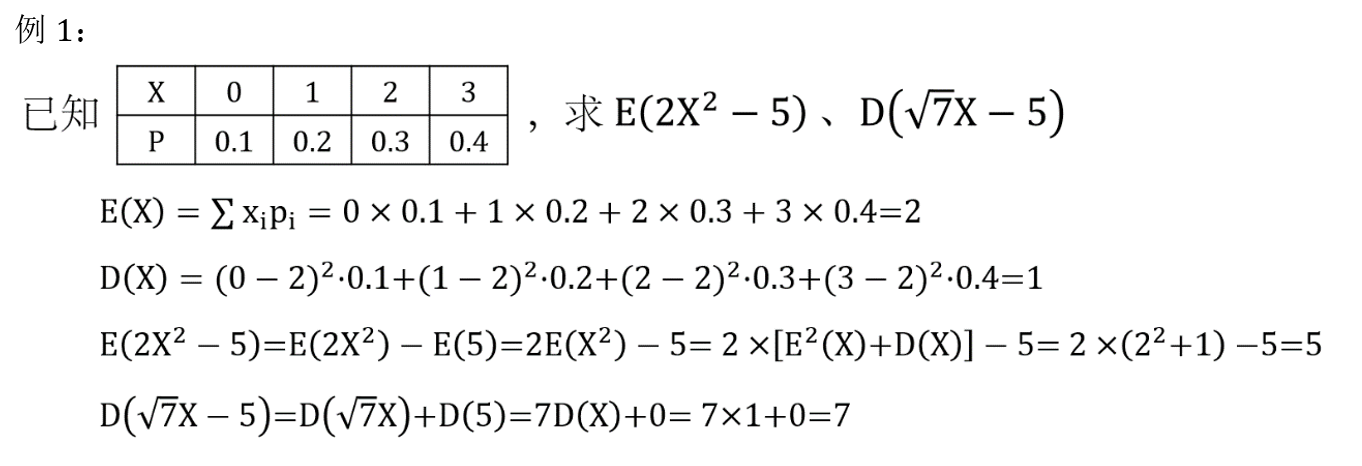
6. E ( X ) 、 D ( X ) E(X)、D(X) E(X)、D(X) 与各种分布的综合题 ⭐

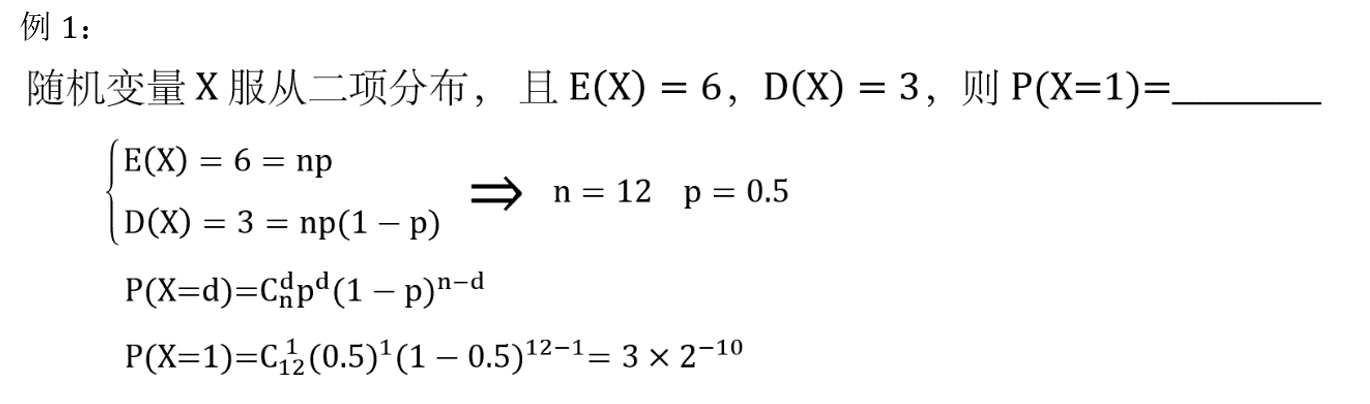

七、中心极限定理



八、区间估计
⭐ 置信区间


⭐ 求置信区间


九、 假设检验
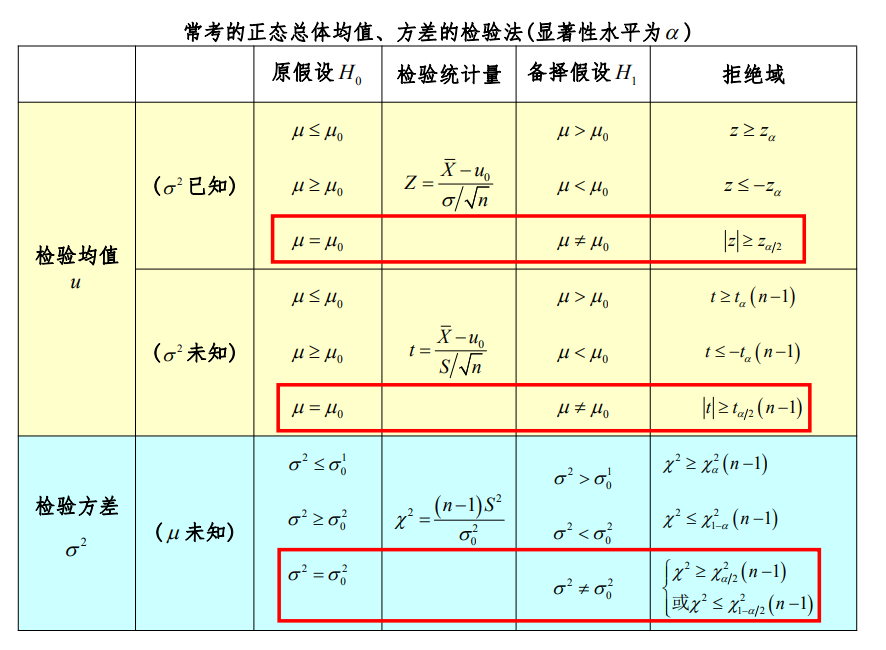
⭐ Z 检验

⭐ t 检验

⭐ x 2 x^2 x2 检验







![[AutoSar]基础部分 RTE 05 Port的实例化和初始化](https://img-blog.csdnimg.cn/direct/bd03a146e3c74accaf19538dcb1261ef.png)