纳什议价解
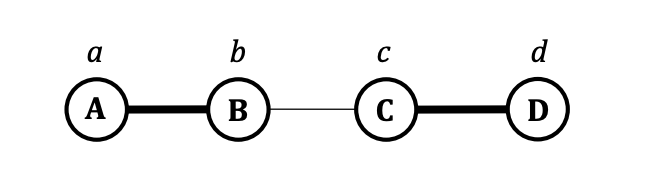
局中人在网络中所处的位置决定了他们的议价权,并最终导致不同的局中人在博弈中所获得的收益大小不同。下图给出了A、B、 C、D 四人参加网络交换博弈的一个稳定结局,其中粗线相连的节点之间达成交换,交换所得效益标记在了节点上方。请按照纳什议价解的计算方式计算出四人的收益,从而得到一个均衡结局
当以下条件成立时,达到均衡
s = 1 − x − y x + s 2 = 1 + x − y 2 y + s 2 = 1 − x + y 2 \begin{aligned} s&=1-x-y\\ x+\frac{s}{2}&=\frac{1+x-y}{2}\\ y+\frac{s}{2}&=\frac{1-x+y}{2} \end{aligned} sx+2sy+2s=1−x−y=21+x−y=21−x+y
解: 如图所示,A 和 B 达成交易,C 和 D 达成交易。A 和 D 处于网络边缘,备选项收益为 0。B 的备选项是和 C 进行交易,备选项收益为 1 − c 1-c 1−c。C 的备选项是和 B 进行交易,备选项收益为 1 − b 1-b 1−b。
根据纳什议价解的公式,存在
对于A:
a
=
0
+
1
2
(
1
−
0
−
(
1
−
c
)
)
=
c
2
a=0+\frac{1}{2}\big(1-0-(1-c)\big)=\frac{c}{2}
a=0+21(1−0−(1−c))=2c
对于B:
b
=
1
−
c
+
1
2
(
1
−
0
−
(
1
−
c
)
)
=
1
−
c
2
b=1-c+\frac{1}{2}(1-0-(1-c))=1-\frac{c}{2}
b=1−c+21(1−0−(1−c))=1−2c
对于C:
c
=
1
−
b
+
1
2
(
1
−
0
−
(
1
−
b
)
)
=
1
−
b
2
c=1-b+\frac12\big(1-0-(1-b)\big)=1-\frac b2
c=1−b+21(1−0−(1−b))=1−2b
对于D:
d
=
0
+
1
2
(
1
−
0
−
(
1
−
b
)
)
=
b
2
d=0+\frac12(1-0-(1-b))=\frac b2
d=0+21(1−0−(1−b))=2b
另外,由于A 和 B 达成交易,C 和 D 达成交易,有
a
+
b
=
1
,
c
+
d
=
1
\mathrm{a+ b= 1},\mathrm{c+ d= 1}
a+b=1,c+d=1 联立上述几个等式, 解线性方程组可得
a
=
1
3
;
b
=
2
3
;
c
=
2
3
;
d
=
1
3
;
a=\frac13;b=\frac23;c=\frac23;d=\frac13;
a=31;b=32;c=32;d=31;