C#，数值计算，基础函数——任意位数π的数值算法源程序与数据可视化

对于数学常数 PI 后面位数的计算与追求，是数学家与计算机科学家们乐此不疲的游戏。

一、圆周率PI简史

圆周率（Pi）是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比，是精确计算圆周长、圆面积、球体积等几何形状的关键值。

圆周率用希腊字母π（读作[paɪ]）表示，是一个常数（约等于3.141592654），是代表圆周长和直径的比值。它是一个无理数，即无限不循环小数。在日常生活中，通常都用3.14代表圆周率去进行近似计算。而用九位小数3.141592654便足以应付一般计算。即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百个位。

古希腊大数学家阿基米德（公元前287年—公元前212年）开创了人类历史上通过理论计算圆周率近似值的先河。阿基米德从单位圆出发，先用内接正六边形求出圆周率的下界为3，再用外接正六边形并借助勾股定理求出圆周率的上界小于4。接着，他对内接正六边形和外接正六边形的边数分别加倍，将它们分别变成内接正12边形和外接正12边形，再借助勾股定理改进圆周率的下界和上界。他逐步对内接正多边形和外接正多边形的边数加倍，直到内接正96边形和外接正96边形为止。最后，他求出圆周率的下界和上界分别为223/71和22/7，并取它们的平均值3.141851为圆周率的近似值。阿基米德用到了迭代算法和两侧数值逼近的概念，称得上是“计算数学”的鼻祖。

中国古算书《周髀算经》（约公元前2世纪）的中有“径一而周三”的记载，意即取。汉朝时，张衡得出，即（约为3.162）。这个值不太准确，但它简单易理解。

公元263年，中国数学家刘徽用“割圆术”计算圆周率，他先从圆内接正六边形，逐次分割一直算到圆内接正192边形。他说：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”这包含了求极限的思想。刘徽给出π=3.141024的圆周率近似值，刘徽在得圆周率=3.14之后，将这个数值和晋武库中汉王莽时代制造的铜制体积度量衡标准嘉量斛的直径和容积检验，发现3.14这个数值还是偏小。于是继续割圆到1536边形，求出3072边形的面积，得到令自己满意的圆周率。

公元480年左右，南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果，给出不足近似值3.1415926和过剩近似值3.1415927，还得到两个近似分数值，密率和约率。密率是个很好的分数近似值，要取到才能得出比略准确的近似。在之后的800年里祖冲之计算出的π值都是最准确的。

其中的密率在西方直到1573年才由德国人奥托（Valentinus Otho）得到，1625年发表于荷兰工程师米托尼斯（Metius）的著作中，欧洲称之为Metius' number。

1665年，英国数学家约翰·沃利斯（John Wallis）出版了一本数学专著，其中他推导出一个公式，发现圆周率等于无穷个分数相乘的积。

2015年，罗切斯特大学的科学家们在氢原子能级的量子力学计算中发现了圆周率相同的公式。

2019年3月14日，谷歌宣布圆周率现已到小数点后31.4万亿位。

二、PI的当前世界纪录

2021年8月17日，美国趣味科学网站报道，瑞士研究人员使用一台超级计算机，历时108天，将著名数学常数圆周率π计算到小数点后62.8万亿位，创下该常数迄今最精确值记录。

三、一些PI值

下面给出一些可能用到的PI值。

1、4位PI

PI=3.1415

2、16位PI

PI=3.1415926535897932

3、64位PI

PI=3.1415926535897932384626433832795028841971693993751058209749445923

4、128位PI

PI=3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460

5、256位PI

6、512位PI

7、1024位PI

8、2048位PI

PI=3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661300192787661119590921642019893809525720106548586327886593615338182796823030195203530185296899577362259941389124972177528347913151557485724245415069595082953311686172785588907509838175463746493931925506040092770167113900984882401285836160356370766010471018194295559619894676783744944825537977472684710404753464620804668425906949129331367702898915210475216205696602405803815019351125338243003558764024749647326391419927260426992279678235478163600934172164121992458631503028618297455570674983850549458858692699569092721079750930295532116534498720275596023648066549911988183479775356636980742654252786255181841757467289097777279380008164706001614524919217321721477235014144197356854816136115735255213347574184946843852332390739414333454776241686251898356948556209921922218427255025425688767179049460165346680498862723279178608578438382796797668145410095388378636095068006422512520511739298489608412848862694560424196528502221066118630674427862203919494504712371378696095636437191728746776465757396241389086583264599581339047802759009946576407895126946839835259570982582262052248940

四、用家里的台式机创造记录的代码

前面说了：2021年8月17日，瑞士研究人员使用一台超级计算机，历时108天，将著名数学常数圆周率π计算到小数点后62.8万亿位，创下该常数迄今最精确值记录。

显然，你我都没有超级计算机。

但是！但是！但是！即使是家里的台式机没准也可以创造世界记录。

1、运行效果

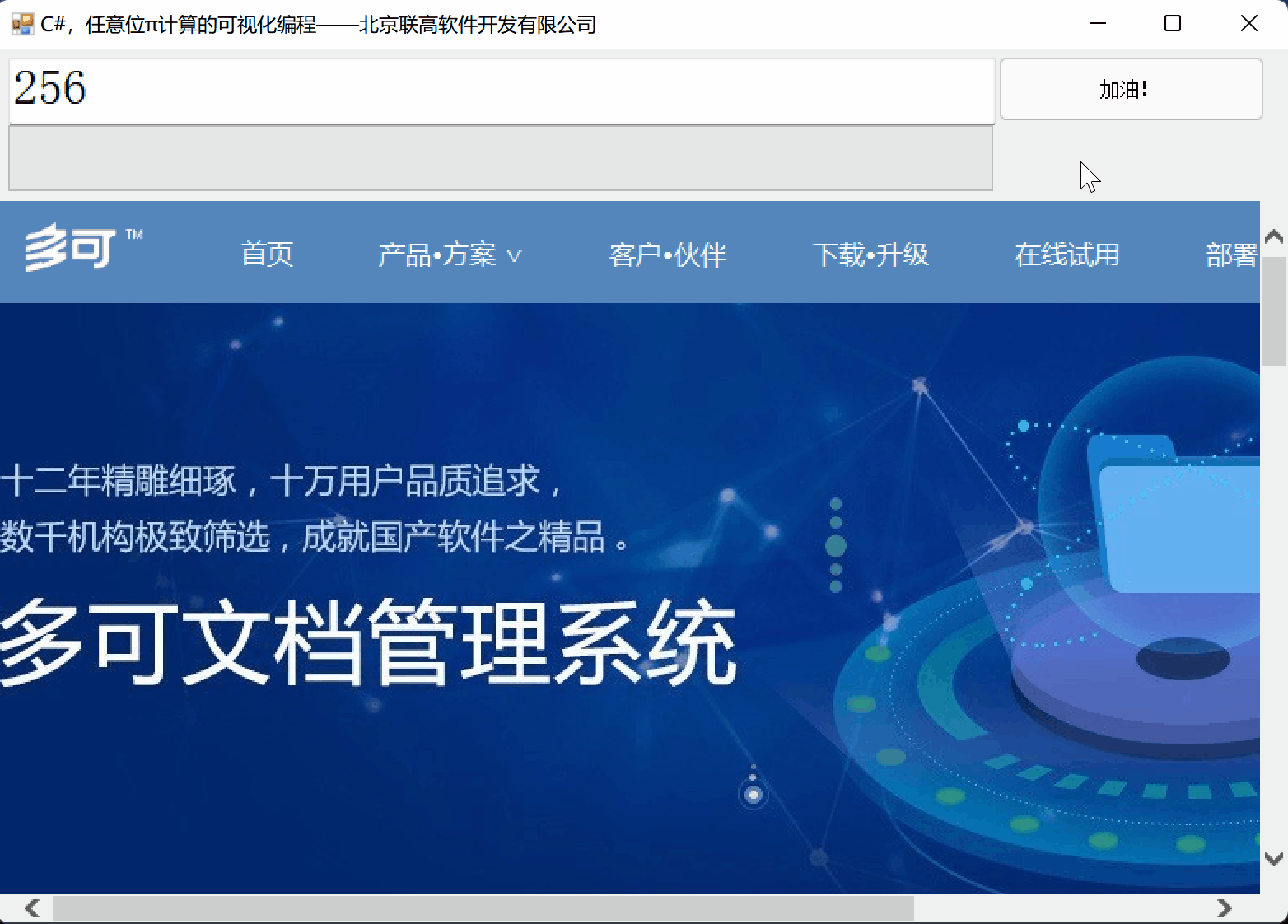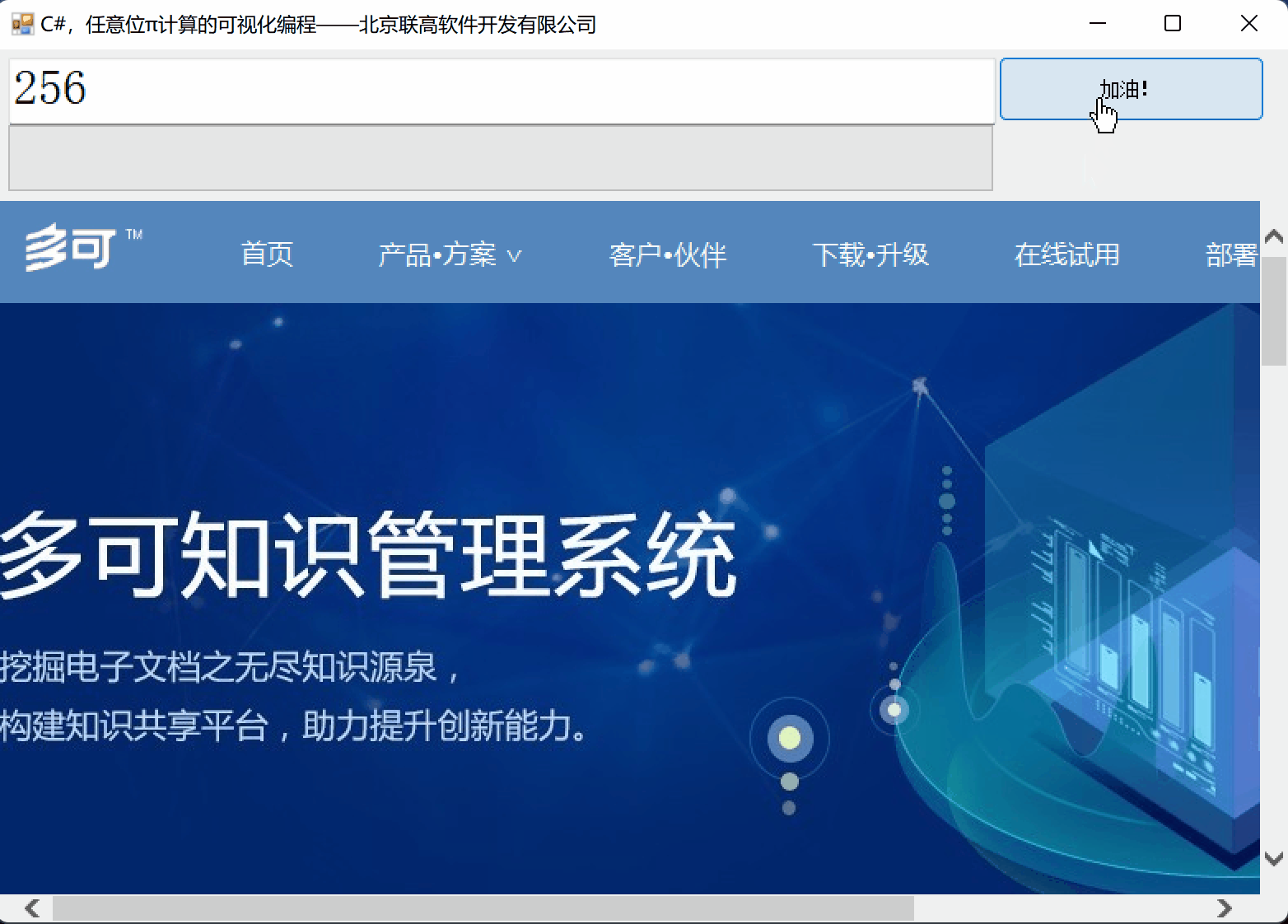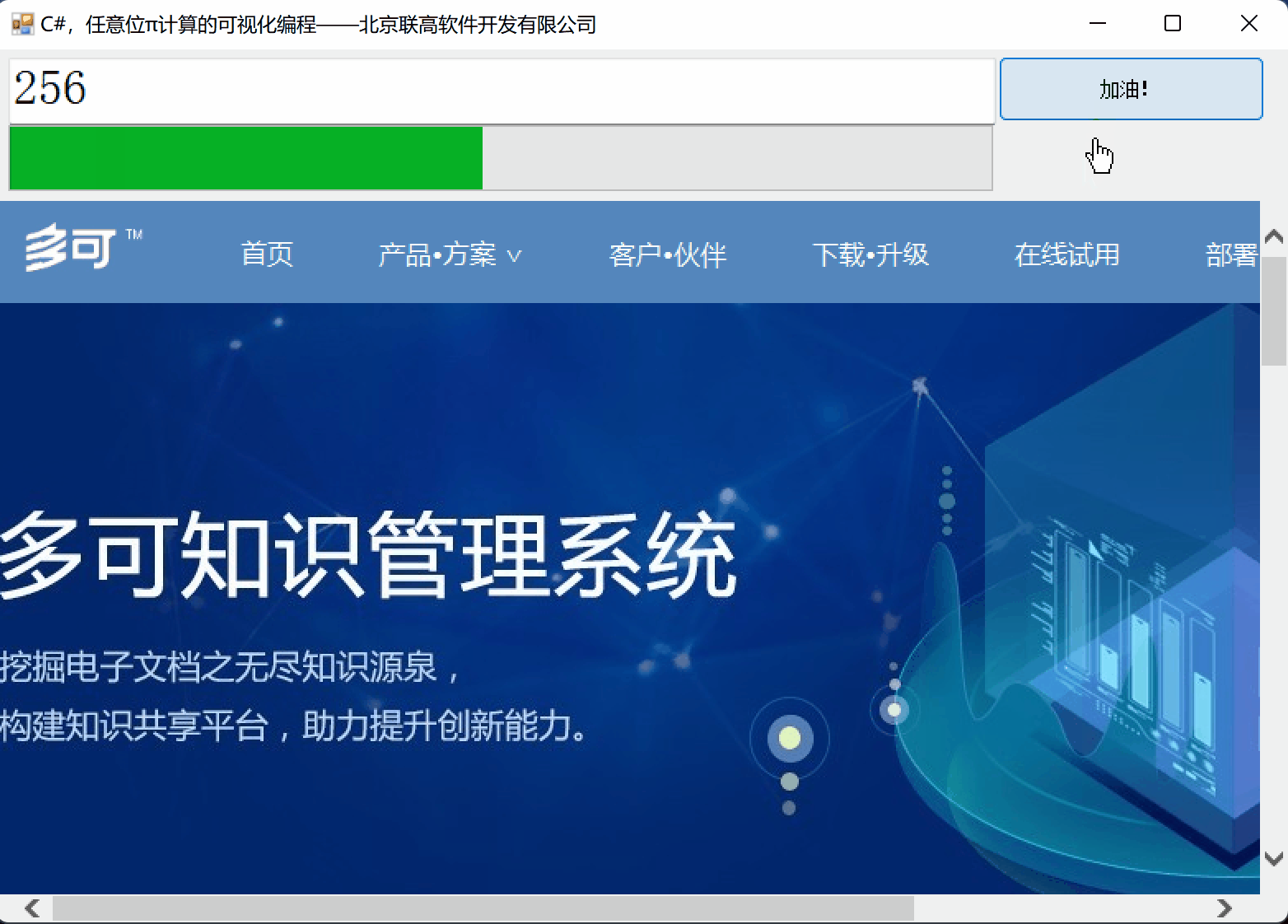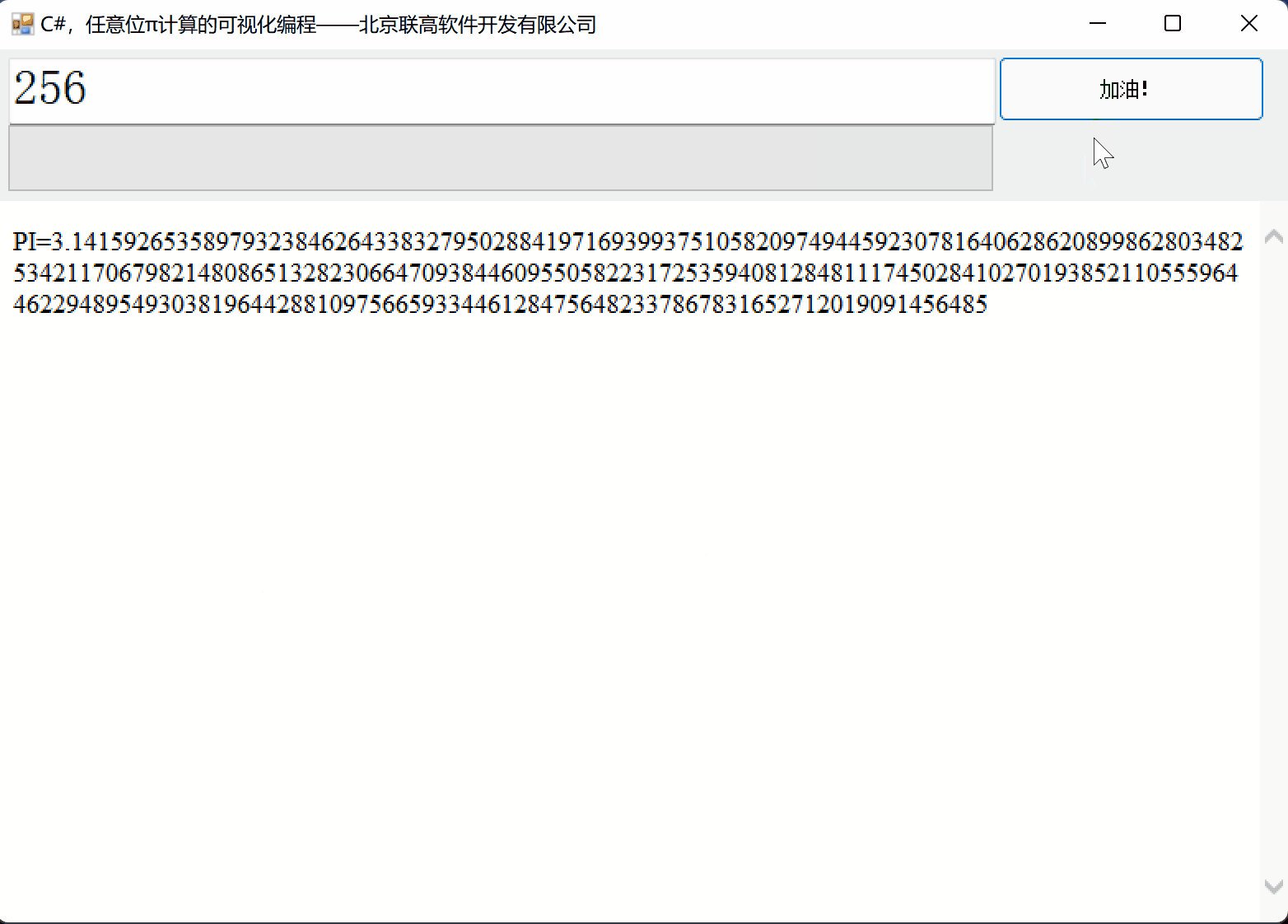
C# 的代码，分为两部分：

2、Windows Form 部分代码

using System;
using System.Text;
using System.Windows.Forms;

using Legalsoft.Alrorithm.Large;

namespace WindowsFormsApp7
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void Form1_Load(object sender, EventArgs e)
        {
            this.Text = "C#，任意位π计算的可视化编程——北京联高软件开发有限公司";
            button1.Text = "加油！"; button1.Cursor = Cursors.Hand;
            textBox1.Text = "256";
            panel1.Dock = DockStyle.Top;
            panel2.Dock = DockStyle.Fill;
            webBrowser1.Navigate("http://www.315soft.com");
        }

        private void button1_Click(object sender, EventArgs e)
        {
            PIer lp = new PIer();
            int n = Int32.Parse("0" + textBox1.Text);
            // 安排一个进度条，超过512位的计算变得慢了，以便看到计算进度！
            progressBar1.Value = 0;
            progressBar1.Maximum = n + 1;
            progressBar1.Style = ProgressBarStyle.Continuous;
            StringBuilder sb = new StringBuilder();
            sb.Append("<html><body style='word-break:break-all;'>");
            sb.Append("PI=3.");
            for (int i = 1; i <= n; i++)
            {
                sb.Append(lp.Execute(i));
                progressBar1.Value = i;
                progressBar1.Refresh();
            }
            sb.Append("</body></html>");
            progressBar1.Value = 0;
            webBrowser1.DocumentText = sb.ToString();
        }
    }
}

3、任意位PI计算的C#代码

（改编自Pi Formulas, Algorithms and Computations (bellard.org)）

using System;

namespace Legalsoft.Alrorithm.Large
{
	public class PIer
	{
		private int InverseXModuleY(int x, int y)
		{
			int u = x;
			int v = y;
			int c = 1;
			int a = 0;
			do
			{
				int q = v / u;
				int t = c;
				c = a - q * c; a = t; t = u;
				u = v - q * u; v = t;
			} while (u != 0);
			a = a % y;
			if (a < 0) { a = y + a; }
			return a;
		}
		private int MultiplyModule(int a, int b, int m)
		{
			return (int)(FloatModule((double)a * (double)b, m));
		}
		private int PowModule(int a, int b, int m)
		{
			int r = 1;
			int aa = a;
			while (true)
			{
				if ((b & 1) != 0) { r = MultiplyModule(r, aa, m); }
				b = b >> 1;
				if (b == 0) { break; }
				aa = MultiplyModule(aa, aa, m);
			}
			return r;
		}
		private int IsPrime(int n)
		{
			int r, i;
			if ((n % 2) == 0) { return 0; }
			r = (int)(Math.Sqrt(n));
			for (i = 3; i <= r; i += 2)
			{
				if ((n % i) == 0) { return 0; }
			}
			return 1;
		}
		private int NextPrime(int n)
		{
			do { n++; } while (IsPrime(n) == 0);
			return n;
		}
		private double FloatModule(double a, double b)
		{
			return (a - (int)(a / b) * b);
		}
		public int Execute(int n)
		{
			double sum = 0.0;
			int N = (int)((n + 20) * Math.Log(10) / Math.Log(2));
			for (int a = 3; a <= (2 * N); a = NextPrime(a))
			{
				int vmax = (int)(Math.Log(2 * N) / Math.Log(a));
				int av = 1;
				for (int i = 0; i < vmax; i++)
				{
					av = av * a;
				}
				int s = 0;
				int num = 1;
				int den = 1;
				int v = 0;
				int kq = 1;
				int kq2 = 1;
				int t;
				for (int k = 1; k <= N; k++)
				{
					t = k;
					if (kq >= a)
					{
						do
						{
							t = t / a; v--;
						} while ((t % a) == 0);
						kq = 0;
					}
					kq++;
					num = MultiplyModule(num, t, av);
					t = (2 * k - 1);
					if (kq2 >= a)
					{
						if (kq2 == a)
						{
							do
							{
								t = t / a; v++;
							} while ((t % a) == 0);
						}
						kq2 -= a;
					}
					den = MultiplyModule(den, t, av);
					kq2 += 2;
					if (v > 0)
					{
						t = InverseXModuleY(den, av);
						t = MultiplyModule(t, num, av);
						t = MultiplyModule(t, k, av);
						for (int i = v; i < vmax; i++)
						{
							t = MultiplyModule(t, a, av);
						}
						s += t;
						if (s >= av) { s -= av; }
					}
				}
				t = PowModule(10, n - 1, av);
				s = MultiplyModule(s, t, av);
				sum = FloatModule(sum + (double)s / (double)av, 1.0);
			}
			return (int)(Math.Floor((int)(sum * 1e9) / 1e8));
		}
	}
}

150行！不多！