二叉树无论是在实际运用还是面试题中,都是一种十分热门的数据结构,而二叉搜索树则是进阶版的二叉树,在map和set中也有应用。
什么是二叉搜索树
二叉搜索树又叫二叉排序树,它可以是一颗空树,又或者是有以下三个特点的树。
- 若它的左子树不为空,则左子树的所有节点的值都小于根节点的值。
- 若它的右子树不为空,则右子树的所有节点的值都大于根节点的值。
- 它的左右子树也都是二叉搜索树。
因为二叉搜索树具有以上三个特性,因此二叉搜索树的最优搜索次数为 O(log^2) ,最差搜索次数为 O(N)。
此外,中序遍历一个二叉搜索树所得到的结果应该是一个有序的数组。
二叉搜索树的实现
二叉搜索树的查找
- 从根节点开始查找,若查找的 val 大于根节点的值,则向右子树查找,否则向左子树查找
- 最多查找高度次,走到空还没有找到,就返回nullptr,否则就返回这个节点。
pNode find(const T& val)
{
pNode cur = Root;
if (cur->_data == val)
{
return cur;
}
while (cur != nullptr)
{
if (val > cur->_data)
{
cur = cur->_right;
}
else if (val < cur->_data)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}二叉搜索树的插入
二叉树的插入需要找到正确的位置。
- val大于当前节点的值就向右子树走
- val小于当前节点的值就向左子树走
- 直到找到一个空节点就插入
bool insert(T val)
{
pNode cur = new Node(val);
pNode root = Root;
if (Root!=nullptr&&find(val) != nullptr)
{
return false;
}
if (root == nullptr)
{
Root = cur;
return true;
}
while (root != nullptr)
{
if (val > root->_data)
{
if (root->_right == nullptr)
{
root->_right = cur;
break;
}
root = root->_right;
}
else if (val < root->_data)
{
if (root->_left == nullptr)
{
root->_left = cur;
break;
}
root = root->_left;
}
}
return true;
}二叉搜索树的删除
二叉搜索树的删除是最难的,需要分情况说明。
- 左子树为空,但右子树不为空
- 右子树为空,但左子树不为空
- 左右都为空
- 左右都不为空
对于最后一种情况来说,这个节点是一个叶子节点,可以直接删除。
右为空左不为空
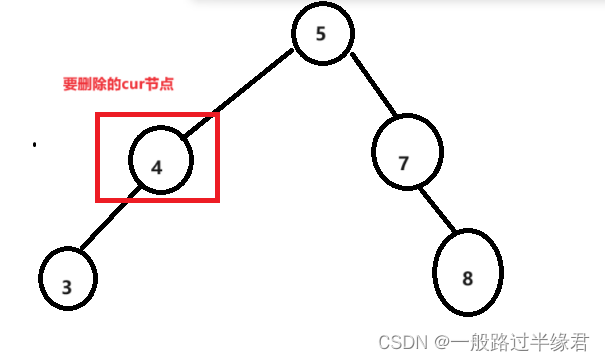
当 cur 节点是父节点的左子树,就需要将父节点的左向量连接在cur节点的左子树上。

反之当cur节点是父节点的右子树,就需要将父节点的右向量连接在cur节点的左子树上。
左为空右不为空
若cur节点的左子树为空,且cur节点是父节点的左子树,就需要将父节点的左向量连接在cur节点的右子树上。

若cur节点是父节点的右子树,则需要将父节点的右向量连接在cur节点的右子树上。

左右不为空
若节点的左右子树都不是空树,为了不破坏二叉搜索树的结构,就需要利用一个中间变量(minright)来辅助删除。
minright应是被删节点的右子树中的最左节点。
1:若minright是被删节点的右节点。

这种情况下就直接交换cur和minright 的值,然后让cur 的右指针指向 minright 的右节点。
2:minright不是被删节点的右节点。

这种情况下,就需要记录 minright 的 parent 节点,让 parent 的左指针指向 minright 的右节点。
然后再交换 cur 和 minright 的值,再删除 minright 的节点。
bool erase(T val)
{
pNode cur = Root;
pNode parent = nullptr;
while (cur != nullptr)
{
//大于向右走
if (val > cur->_data)
{
parent = cur;
cur = cur->_right;
}
//小于向左走
else if (val < cur->_data)
{
parent = cur;
cur = cur->_left;
}
//等于则开始消除
else
{
if (cur->_right == nullptr)
{
//如果是根节点,就直接拿左节点当根
if (cur == Root)
{
Root = cur->_left;
}
//否则就正常进行
else
{
//如果cur是parent的右节点,就直接拿cur的左节点和parent的右节点相连
if (cur == parent->_right)
{
parent->_right = cur->_left;
}
//如果cur是parent的左节点,就拿cur的左节点和parent的左节点相连
else if (cur == parent->_left)
{
parent->_left = cur->_left;
}
}
delete cur;
}
else if (cur->_left == nullptr)
{
//如果是根节点
if (cur == Root)
{
Root = cur->_right;
}
//否则就正常进行
else
{
//如果cur是parent的右节点,就直接拿cur的左节点和parent的右节点相连
if (cur == parent->_right)
{
parent->_right = cur->_right;
}
//如果cur是parent的左节点,就拿cur的左节点和parent的左节点相连
else if (cur == parent->_left)
{
parent->_left = cur->_right;
}
}
delete cur;
}
//左右都不为空
else
{
pNode minright = cur->_right;
parent = cur;
while (minright->_left)
{
parent = minright;
minright = minright->_left;
}
cur->_data = minright->_data;
if (minright == parent->_right)
{
parent->_right = minright->_right;
}
else
{
parent->_left = minright->_right;
}
delete minright;
}
return true;
}
}
return false;
}
完整代码
using namespace std;
template<class T>
class BSTNode {
public:
BSTNode(T data)
:_left(nullptr),_right(nullptr),_data(data)
{
}
T _data;
BSTNode<T>* _left;
BSTNode<T>* _right;
};
template<class T>
class BSTree {
typedef BSTNode<T> Node;
typedef Node* pNode;
public:
BSTree()
:Root(nullptr)
{}
~BSTree()
{
destroy(Root);
}
void destroy(pNode root)
{
if (root->_left != nullptr)
{
destroy(root->_left);
}
if (root->_right != nullptr)
{
destroy(root->_right);
}
delete(root);
}
pNode find(const T& val)
{
pNode cur = Root;
if (cur->_data == val)
{
return cur;
}
while (cur != nullptr)
{
if (val > cur->_data)
{
cur = cur->_right;
}
else if (val < cur->_data)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool erase(T val)
{
pNode cur = Root;
pNode parent = nullptr;
while (cur != nullptr)
{
//大于向右走
if (val > cur->_data)
{
parent = cur;
cur = cur->_right;
}
//小于向左走
else if (val < cur->_data)
{
parent = cur;
cur = cur->_left;
}
//等于则开始消除
else
{
if (cur->_right == nullptr)
{
//如果是根节点,就直接拿左节点当根
if (cur == Root)
{
Root = cur->_left;
}
//否则就正常进行
else
{
//如果cur是parent的右节点,就直接拿cur的左节点和parent的右节点相连
if (cur == parent->_right)
{
parent->_right = cur->_left;
}
//如果cur是parent的左节点,就拿cur的左节点和parent的左节点相连
else if (cur == parent->_left)
{
parent->_left = cur->_left;
}
}
delete cur;
}
else if (cur->_left == nullptr)
{
//如果是根节点
if (cur == Root)
{
Root = cur->_right;
}
//否则就正常进行
else
{
//如果cur是parent的右节点,就直接拿cur的左节点和parent的右节点相连
if (cur == parent->_right)
{
parent->_right = cur->_right;
}
//如果cur是parent的左节点,就拿cur的左节点和parent的左节点相连
else if (cur == parent->_left)
{
parent->_left = cur->_right;
}
}
delete cur;
}
//左右都不为空
else
{
pNode minright = cur->_right;
parent = cur;
while (minright->_left)
{
parent = minright;
minright = minright->_left;
}
cur->_data = minright->_data;
if (minright == parent->_right)
{
parent->_right = minright->_right;
}
else
{
parent->_left = minright->_right;
}
delete minright;
}
return true;
}
}
return false;
}
bool insert(T val)
{
pNode cur = new Node(val);
pNode root = Root;
if (Root!=nullptr&&find(val) != nullptr)
{
return false;
}
if (root == nullptr)
{
Root = cur;
return true;
}
while (root != nullptr)
{
if (val > root->_data)
{
if (root->_right == nullptr)
{
root->_right = cur;
break;
}
root = root->_right;
}
else if (val < root->_data)
{
if (root->_left == nullptr)
{
root->_left = cur;
break;
}
root = root->_left;
}
}
return true;
}
private:
pNode Root;
};总结
二叉搜索树是一种进阶版的二叉树结构,实际应用中十分广泛,面试题中经常出现,而在二叉搜索树之上还有AVL树和红黑树,不过这些都是后话了。