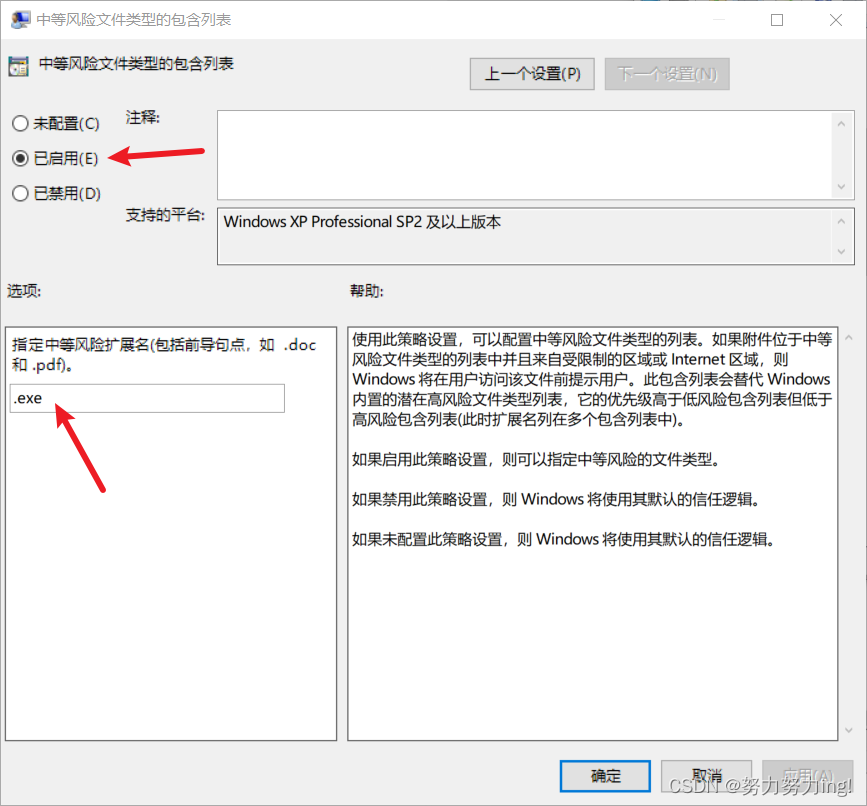
继续预习O.o
从这一章开始看自己班发的 PPT 了
LL(1)的部分因为班里发了所以又看了一遍hhh感觉比之前那个清楚一点
目录
I. 自顶向下
一、概念(看一眼)
1、语法分析的两大类分析方法
2、算法基本思想
3、自顶向下介绍
1)一般过程
2)主要问题 回溯(分类是 确定的、不确定的 → 回溯)
① 定义及影响
② 消除回溯
✿ 提取左因子
✿ 消除左递归(直接间接)
✿✿ 直接
✿✿ 间接(了解)
二、LL(1)
1、定义
1)first 集
2)follow 集
✿ 例题
3)判断条件
4)非LL(1)转LL(1)
2、分析表
3、优缺点
三、递归下降(看一眼)
II. 自底向上
一、概念(看一眼)
1、短语和直接短语(可以不唯一)
2、句柄(唯一)
二、LR(0)
1、概念
2、优缺点
3、分析器
✿ 分析表 * 2
4、算法描述
5、工作过程
1)定义
2)活前缀与句柄
① 定义(没看明白O.o)
② 构造识别活前缀的 dfa (直接构造)
6、判断条件
7、分析表(建议直接做题O.o)
8、问题
三、SLR(1)(升级版LR(0))
1、概念
2、分析表(建议直接做题O.o)
3、问题
III. 符号表(记住基本概念多做题O.o)
IV. 中间代码及语法制导(也是多做题)
一、概念
✿ 逆波兰式
二、三元式(不知道考不考)
三、四元式(要考)
四、回填翻译(一般从100开始写起,做几个题懂了)
I. 自顶向下
一、概念(看一眼)
1、语法分析的两大类分析方法

2、算法基本思想

3、自顶向下介绍
1)一般过程

2)主要问题 回溯(分类是 确定的、不确定的 → 回溯)
① 定义及影响

② 消除回溯
✿ 提取左因子

✿ 消除左递归(直接间接)
✿✿ 直接
因为E推T+T或T-T或T,所以可以改成TE’,但是不知道为什么没写-的情况

✿✿ 间接(了解)

二、LL(1)
1、定义

1)first 集


2)follow 集


✿ 例题
感觉不难但需要做题熟悉一下O.o

3)判断条件
感觉有点繁琐,记得 不含左递归+同一左部产生式的select无交集 就行,之前的笔记里有select的详细求法,简单来说就是,如 A → B,先 看B的first有没有空 :
有 → select(A→B) = 去掉空的first(B) + follow(A)
无 → select(A→B) = first(B)

4)非LL(1)转LL(1)
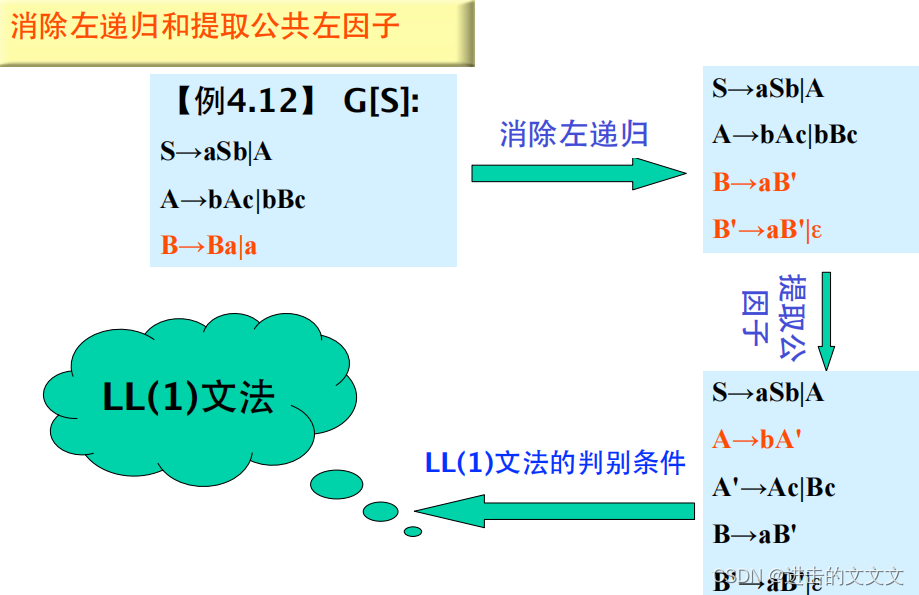
2、分析表

跟连连看差不多(?),拿E'这一行举例,+是因为E'的first有+, )列是因为E'的follow有空,
不填的是因为first和follow都没有
但是我感觉 E' 最后两列应该填 E'→空 来着O.o,等看书的时候看看这一块
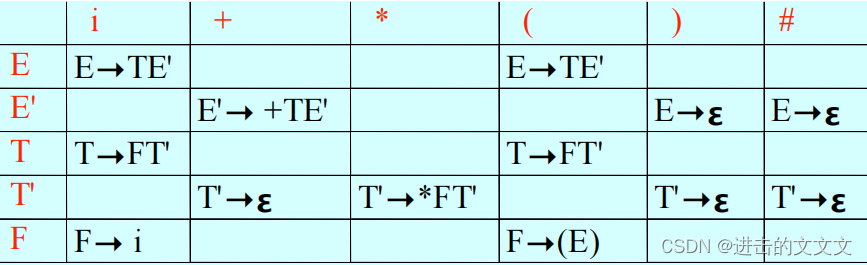
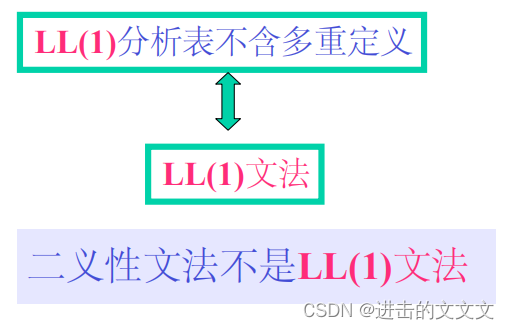
3、优缺点

三、递归下降(看一眼)


II. 自底向上
因为期末只考LR(0)和SLR(1)所以只看了这两个O.o
一、概念(看一眼)
1、短语和直接短语(可以不唯一)

2、句柄(唯一)

终结符,小写字母或符号之类的

二、LR(0)
1、概念

2、优缺点

3、分析器
逻辑结构:分析表、分析栈、总控程序
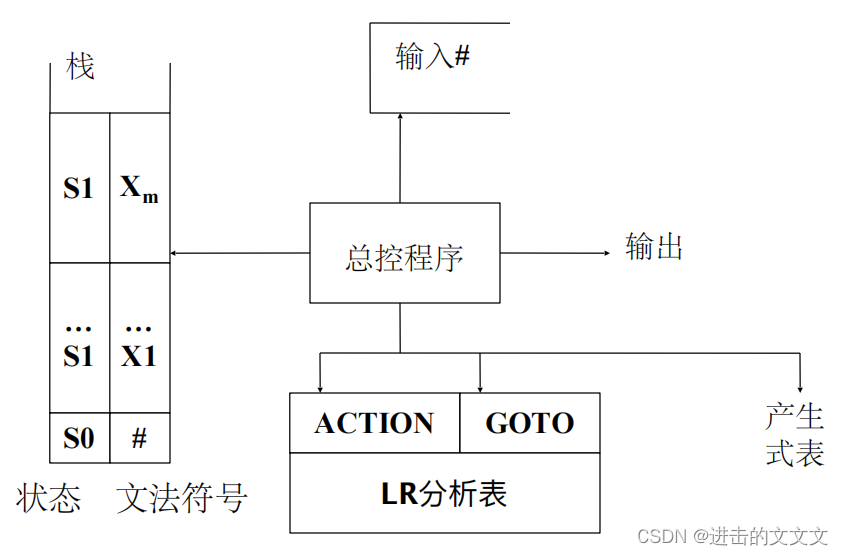
✿ 分析表 * 2

4、算法描述

5、工作过程
1)定义

2)活前缀与句柄
① 定义(没看明白O.o)

② 构造识别活前缀的 dfa (直接构造)
建议直接做题

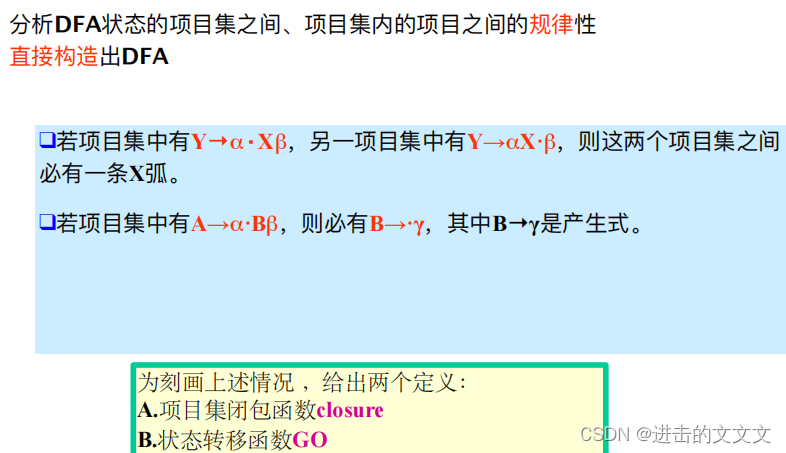

6、判断条件

7、分析表(建议直接做题O.o)
移近s规约r
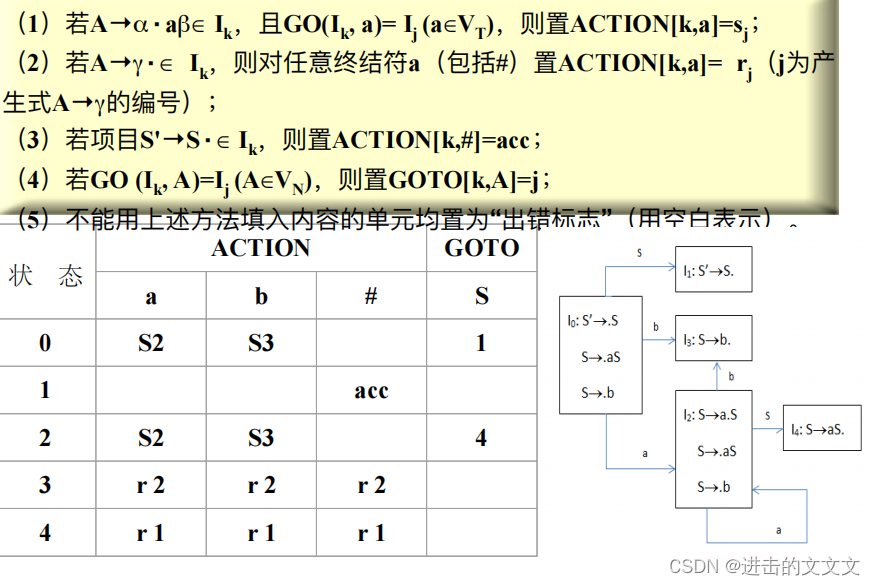
8、问题

三、SLR(1)(升级版LR(0))
1、概念


2、分析表(建议直接做题O.o)

3、问题

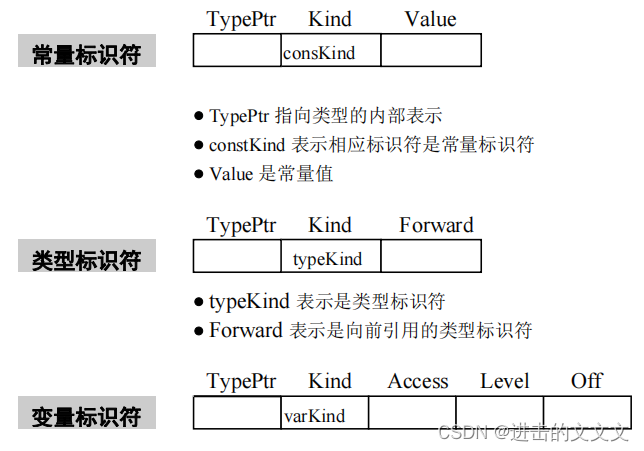
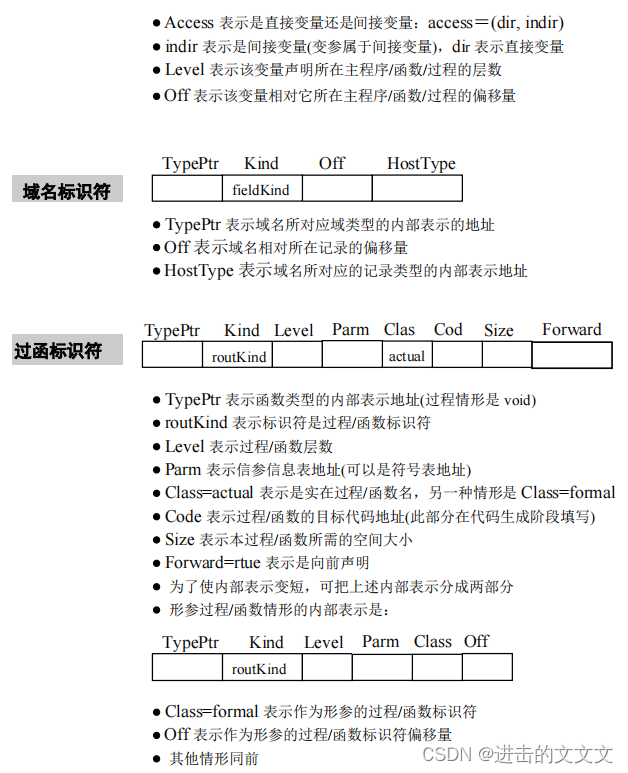
III. 符号表(记住基本概念多做题O.o)


IV. 中间代码及语法制导(也是多做题)
我只考中间代码O.o

一、概念

✿ 逆波兰式
可能出大题,多做几个中缀转后缀的题就行,数据结构学过O.o

二、三元式(不知道考不考)

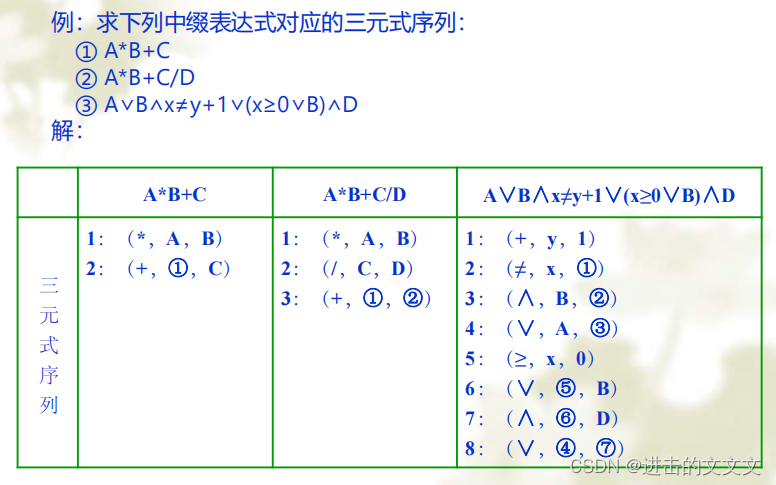
三、四元式(要考)
主要运算顺序就行,优先括号


四、回填翻译(一般从100开始写起,做几个题懂了)
因为例题在书上就略过了O.o
ppt终于全看完了!好耶!明天得开始看课本做习题了O.o
祝大家的期末都高分过~
加油加油!