一、实验目的

1、掌握低通信号的抽样及重建过程；
2、掌握PCM的编码及译码过程。

二、实验内容

共2问：

三、实验程序

1、

function q1()
dt = 0.001;  % 时间分辨率
t = -8 * pi : dt : 8 * pi;  % 时间向量
x_t = cos(0.15 * pi * t) + sin(2.5 * pi * t) + cos(4 * pi * t);  
% 低通信号
[f, x_f] = F(t, x_t);
fs = 4;  % 采样速率
sdt = 1 / fs;  % 采样间隔
t1 = -8 * pi : sdt : 8 * pi;
st = cos(0.15 * pi * t1) + sin(2.5 * pi * t1) + cos(4 * pi * t1);  
% 采样信号
[f1, sf] = F(t1, st);
 
% 恢复原始信号
t2 = -50 : dt : 50;
gt = sinc(fs * t2);
stt = sigexpand(st, sdt / dt);
xt_t = conv(stt, gt);  % 恢复信号
t3 = -50 : dt : 60 + sdt - dt;
 
figure;  % 画出该低通信号的波形
plot(t, x_t);
xlabel('t/s');
ylabel('x(t)');
title('低通信号x(t)的波形');
grid on;
axis([-8 * pi 8 * pi -3 3]);
 
figure;  % 画出抽样序列，抽样速率为4Hz
plot(t1, st);
xlabel('t/s');
ylabel('x_s(t)');
title('抽样速率为4Hz的抽样序列');
grid on;
axis([-8 * pi 8 * pi -2.5 2.5]);
 
figure;  % 画出抽样序列恢复出的原始信号
plot(t3, xt_t(1 : length(t3)));
xlabel('t/s');
ylabel('x\^(t)');
title('抽样序列恢复出的原始信号');
axis([0 50 -2.5 2.5])
grid on;

2、

function q2()
dt = 0.001; % 时间分辨率
t = -4 * pi : dt : 4 * pi;  % 时间向量
xt = sin(2 * pi * t);  % 低通信号
fs = 20;  % 采样频率
sdt = 1 / fs; % 采样间隔
t1 = -4 * pi : sdt : 4 * pi;  % 采样时间向量
st = sin(2 * pi * t1);  % 采样信号
 
ct = [];
Dt = [];
for i = 1 : length(t1)  % 对每一个采样点进行迭代
    mt = st(i) / 1 * 4096;  % 转化为量化电平
    bt = pcm_encode(mt);  % 进行pcm编码
    ct = cat(2, bt, ct);
    dt = pcm_decode(bt, 1);  % 进行pcm解码
    Dt(i) = dt;
end
c1 = [];
for j = 1 : 50
    if ct(j) == 0
        c = zeros(1, 20);
    elseif ct(j) == 1
        c = ones(1, 20);
    end
    c1 = [c1 c];
end
 
figure;  % 画出未编码波形
plot(t1, st);
xlabel('t/s');
ylabel('x_s(t)');
title('未编码波形');
grid on;
axis([-4 * pi 4 * pi -1 1]);
 
figure;  % 画出PCM编码后的波形
plot(t1, c1(1 : length(t1)));
xlabel('t/s');
ylabel('PCM(t)');
title('经过PCM编码的波形');
grid on;
axis([-12 10 -0.1 1.1]);
 
figure;  %画出译码后的波形
plot(t1, Dt);
xlabel('t/s');
ylabel('x\^(t)');
title('译码后的波形');
grid on;
axis([-4 * pi 4 * pi -1 1]);

function q2_2()
cnt = -70 : 1 : 0;
for i = 1 : length(cnt)
    Ac = 10 ^ (cnt(i) / 20);  % dB的转换
    r(i) = PCM(Ac);
end
plot(cnt, 10 * log10(r));
grid on;
xlabel('A_c^2/A_0^2');
ylabel('r/dB');
title('量化信噪比与SNR的关系曲线');
end

程序中用到的子函数：

1、

function [f, sf] = F(t, st)
%利用fft, fftshift定义函数F计算信号的傅里叶变换
%t-离散时间
%st-离散信号
dt = t(2) - t(1); %时间分辨率
T = t(end);
df = 1 / T; %频率分辨率
N = length(st); %离散傅里叶变换长度
f = -N / 2 * df : df : N / 2 * df - df;
sf = fft(st);
sf = T / N * fftshift(sf);

2、

function [out] = sigexpand(d, M)
%将输入的序列扩展为间隔为N – 1个0的序列
%M：系统采样频率
%d：输入的二进制代码
%out：为1 * (M * length(d))维的矩阵
N = length(d);
out = zeros(M, N);
out(1, :) = d;
out = reshape(out, 1, M * N);
end

3、

function [out] = PCM(Ac)
v = 1;  % 过载电平
t = 0 : 0.01 : 10;
s = Ac * sin(2 * pi * t);  % 抽样序列
y = floor(s / v * 4096);  % 信号值转化为量化单位
pcm_en = pcm_encode(y);  % pcm编码
pcm_de = pcm_decode(pcm_en, v);  % pcm译码
Nq = mean((s - pcm_de).^2);  % 计算量化噪声功率
S = mean(s .^ 2);  % 计算信号平均功率
out = S / Nq;
end

4、

function [out] = pcm_encode(x)
% 输入x参数为0~4096的样值，输出out为8位二进制码
n = length(x);
for i = 1 : n
    % 编写段落码
    if x(i) > 0
        out(i, 1) = 1;
    else
        out(i, 1) = 0;
    end
    % 编写段内码计算量化间隔和量化起始电平
    if abs(x(i)) > 0 && abs(x(i)) < 32
        %段落码
        out(i, 2) = 0;
        out(i, 3) = 0;
        out(i, 4) = 0;
        % 量化间隔
        step = 2;
        %起始电平
        st = 0;
    elseif 32 <= abs(x(i)) && abs(x(i)) < 64
        out(i, 2) = 0;
        out(i, 3) = 0;
        out(i, 4) = 1;
        step = 2;
        st = 32;
     elseif 64 <= abs(x(i)) & abs(x(i)) < 128
        out(i, 2) = 0;
        out(i, 3) = 1;
        out(i, 4) = 0;
        step = 4;
        st = 64;
    elseif 128 <= abs(x(i)) & abs(x(i)) < 256
        out(i, 2) = 0;
        out(i, 3) = 1;
        out(i, 4) = 1;
        step = 8;
        st = 128;
    elseif 256 <= abs(x(i)) & abs(x(i)) < 512
        out(i, 2) = 1;
        out(i, 3) = 0;
        out(i, 4) = 0;
        step = 16;
        st = 256;
    elseif 512 <= abs(x(i)) & abs(x(i)) < 1024
        out(i, 2) = 1;
        out(i, 3) = 0;
        out(i, 4) = 1;
        step = 32;
        st = 512;
    elseif 1024 <= abs(x(i)) & abs(x(i)) < 2048
        out(i, 2) = 1;
        out(i, 3) = 1;
        out(i, 4) = 0;
        step = 64;
        st = 1024;
    elseif 2048 <= abs(x(i)) & abs(x(i)) < 4096
        out(i, 2) = 1;
        out(i, 3) = 1;
        out(i, 4) = 1;
        step = 128;
        st = 2048;
    else
        out(i, 2) = 1;
        out(i, 3) = 1;
        out(i, 4) = 1;
        step = 128;
        st = 2048;
    end
    if(abs(x(i)) >= 4096)
        % 处理过载现象
        out(i, 2: 8) = [1 1 1 1 1 1 1];
    else
        % 计算段落码
        tmp = floor((abs(x(i)) - st) / step);
        t = dec2bin(tmp, 4) - 48;
        out(i, 5 : 8) = t(1 : 4);
    end
end
out = reshape(out', 1, 8 * n);

5、

function [out] = pcm_decode(in, v)
% 输入in为8位二进制码，(-v, +v)为量化区间
n = length(in);
in = reshape(in', 8, n / 8)';
slot(1) = 0;
slot(2) = 32;
slot(3) = 64;
slot(4) = 128;
slot(5) = 256;
slot(6) = 512;
slot(7) = 1024;
slot(8) = 2048;
step(1) = 2;
step(2) = 2;
step(3) = 4;
step(4) = 8;
step(5) = 16;
step(6) = 32;
step(7) = 64;
step(8) = 128;
for i = 1 : n / 8
    ss = 2 * in(i, 1) - 1;
    tmp = in(i, 2) * 4 + in(i, 3) * 2 + in(i, 4) + 1;
    st = slot(tmp);
    dt = (in(i, 5) * 8 + in(i, 6) * 4 + in(i, 7) * 2 + in(i, 8)) * step(tmp) + 0.5 * step(tmp);
    out(i) = ss * (st + dt) / 4096 * v;
end

四、实验结果

1、
（1）、低通信号x(t)的波形：

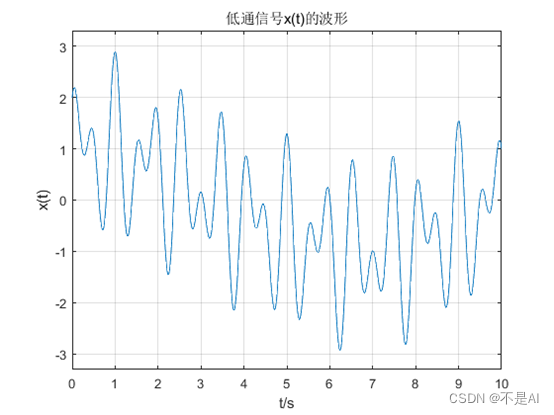
图1
（2）、抽样速率为4Hz的抽样序列：

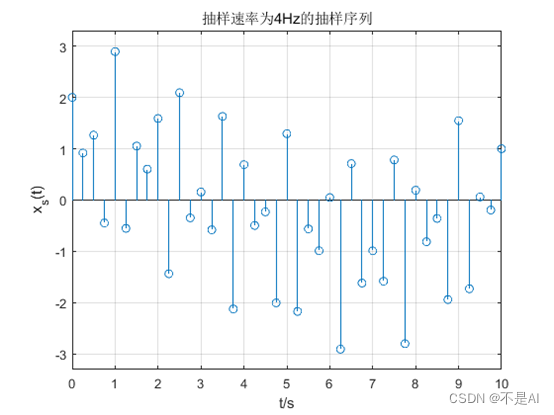
图2
（3）、抽样序列恢复出的原始信号：

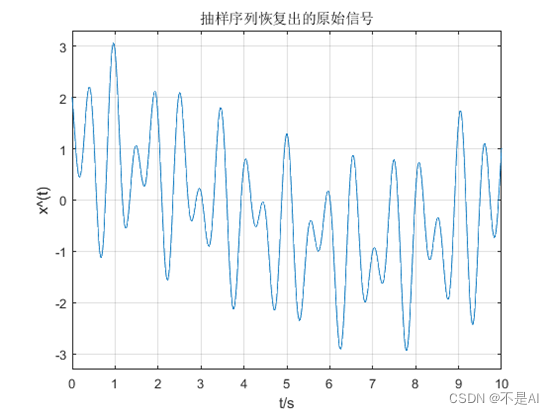
图3
2、
（1）、未编码的波形：

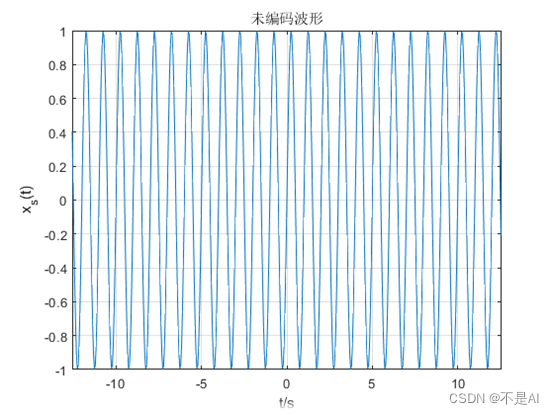
图4
（2）、经过PCM编码后的波形（部分，由于采样点数太多导致无法全部画完）：

图5
（3）、译码后的波形：

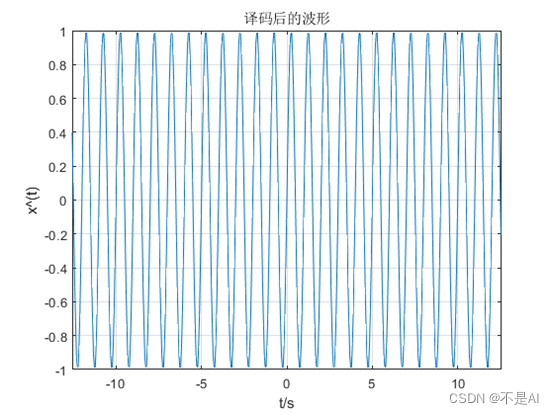
图6
（4）、不同幅度Ac情况下，PCM译码后的量化信噪比：

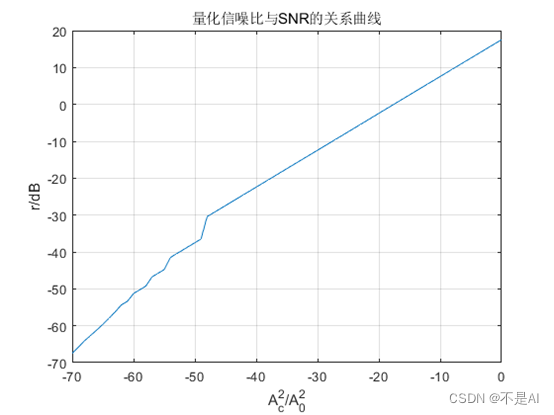
图7

五、实验分析

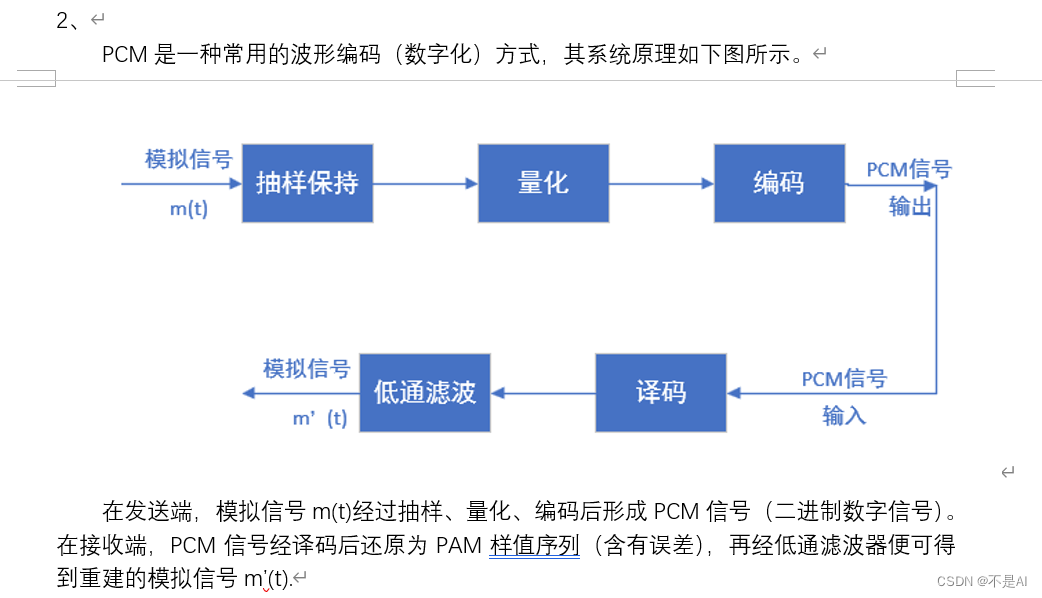
六、参考文献

1、《通信原理（第7版）》，樊昌信 曹丽娜 编著，北京，国防工业出版社，2022年1月。

2、《信号与系统（第二版）》，【美】Alan V. Oppenheim 等 著，刘树棠 译，北京，电子工业出版社，2020年8月。