目录
- 1. 深度循环神经网络
- 2. 双向循环神经网络
- 总结
1. 深度循环神经网络
之前介绍的循环神经网络只有一个单向的隐藏层,在深度学习应用里,我们通常会用到含有多个隐藏层的循环神经网络,也称作深度循环神经网络。下图演示了一个有 L L L个隐藏层的深度循环神经网络,每个隐藏状态不断传递至当前层的下一时间步和当前时间步的下一层。
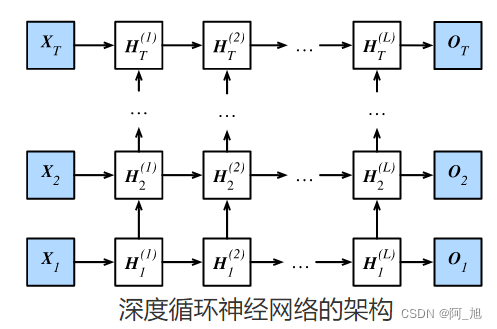
在时间步 t t t里,设小批量输入 X t ∈ R n × d \boldsymbol{X}_t \in \mathbb{R}^{n \times d} Xt∈Rn×d(样本数为 n n n,输入个数为 d d d),第 ℓ \ell ℓ隐藏层( ℓ = 1 , … , L \ell=1,\ldots,L ℓ=1,…,L)的隐藏状态为 H t ( ℓ ) ∈ R n × h \boldsymbol{H}_t^{(\ell)} \in \mathbb{R}^{n \times h} Ht(ℓ)∈Rn×h(隐藏单元个数为 h h h),输出层变量为 O t ∈ R n × q \boldsymbol{O}_t \in \mathbb{R}^{n \times q} Ot∈Rn×q(输出个数为 q q q),且隐藏层的激活函数为 ϕ \phi ϕ。第1隐藏层的隐藏状态和之前的计算一样:
H t ( 1 ) = ϕ ( X t W x h ( 1 ) + H t − 1 ( 1 ) W h h ( 1 ) + b h ( 1 ) ) , \boldsymbol{H}_t^{(1)} = \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(1)} + \boldsymbol{H}_{t-1}^{(1)} \boldsymbol{W}_{hh}^{(1)} + \boldsymbol{b}_h^{(1)}), Ht(1)=ϕ(XtWxh(1)+Ht−1(1)Whh(1)+bh(1)),
其中权重 W x h ( 1 ) ∈ R d × h \boldsymbol{W}_{xh}^{(1)} \in \mathbb{R}^{d \times h} Wxh(1)∈Rd×h、 W h h ( 1 ) ∈ R h × h \boldsymbol{W}_{hh}^{(1)} \in \mathbb{R}^{h \times h} Whh(1)∈Rh×h和偏差 b h ( 1 ) ∈ R 1 × h \boldsymbol{b}_h^{(1)} \in \mathbb{R}^{1 \times h} bh(1)∈R1×h分别为第1隐藏层的模型参数。
当 1 < ℓ ≤ L 1 < \ell \leq L 1<ℓ≤L时,第 ℓ \ell ℓ隐藏层的隐藏状态的表达式为
H t ( ℓ ) = ϕ ( H t ( ℓ − 1 ) W x h ( ℓ ) + H t − 1 ( ℓ ) W h h ( ℓ ) + b h ( ℓ ) ) , \boldsymbol{H}_t^{(\ell)} = \phi(\boldsymbol{H}_t^{(\ell-1)} \boldsymbol{W}_{xh}^{(\ell)} + \boldsymbol{H}_{t-1}^{(\ell)} \boldsymbol{W}_{hh}^{(\ell)} + \boldsymbol{b}_h^{(\ell)}), Ht(ℓ)=ϕ(Ht(ℓ−1)Wxh(ℓ)+Ht−1(ℓ)Whh(ℓ)+bh(ℓ)),
其中权重 W x h ( ℓ ) ∈ R h × h \boldsymbol{W}_{xh}^{(\ell)} \in \mathbb{R}^{h \times h} Wxh(ℓ)∈Rh×h、 W h h ( ℓ ) ∈ R h × h \boldsymbol{W}_{hh}^{(\ell)} \in \mathbb{R}^{h \times h} Whh(ℓ)∈Rh×h和偏差 b h ( ℓ ) ∈ R 1 × h \boldsymbol{b}_h^{(\ell)} \in \mathbb{R}^{1 \times h} bh(ℓ)∈R1×h分别为第 ℓ \ell ℓ隐藏层的模型参数。
最终,输出层的输出只需基于第 L L L隐藏层的隐藏状态:
O t = H t ( L ) W h q + b q , \boldsymbol{O}_t = \boldsymbol{H}_t^{(L)} \boldsymbol{W}_{hq} + \boldsymbol{b}_q, Ot=Ht(L)Whq+bq,
其中权重 W h q ∈ R h × q \boldsymbol{W}_{hq} \in \mathbb{R}^{h \times q} Whq∈Rh×q和偏差 b q ∈ R 1 × q \boldsymbol{b}_q \in \mathbb{R}^{1 \times q} bq∈R1×q为输出层的模型参数。
同多层感知机一样,隐藏层个数 L L L和隐藏单元个数 h h h都是超参数。此外,如果将隐藏状态的计算换成门控循环单元或者长短期记忆的计算,我们可以得到深度门控循环神经网络。
2. 双向循环神经网络
之前介绍的循环神经网络模型都是假设当前时间步是由前面的较早时间步的序列决定的,因此它们都将信息通过隐藏状态从前往后传递。有时候,当前时间步也可能由后面时间步决定。例如,当我们写下一个句子时,可能会根据句子后面的词来修改句子前面的用词。双向循环神经网络通过增加从后往前传递信息的隐藏层来更灵活地处理这类信息。下图演示了一个含单隐藏层的双向循环神经网络的架构。

下面我们来介绍具体的定义。给定时间步 t t t的小批量输入 X t ∈ R n × d \boldsymbol{X}_t \in \mathbb{R}^{n \times d} Xt∈Rn×d(样本数为 n n n,输入个数为 d d d)和隐藏层激活函数为 ϕ \phi ϕ。在双向循环神经网络的架构中,设该时间步正向隐藏状态为 H → t ∈ R n × h \overrightarrow{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h} Ht∈Rn×h(正向隐藏单元个数为 h h h),反向隐藏状态为 H ← t ∈ R n × h \overleftarrow{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h} Ht∈Rn×h(反向隐藏单元个数为 h h h)。我们可以分别计算正向隐藏状态和反向隐藏状态:
H → t = ϕ ( X t W x h ( f ) + H → t − 1 W h h ( f ) + b h ( f ) ) , H ← t = ϕ ( X t W x h ( b ) + H ← t + 1 W h h ( b ) + b h ( b ) ) , \begin{aligned} \overrightarrow{\boldsymbol{H}}_t &= \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(f)} + \overrightarrow{\boldsymbol{H}}_{t-1} \boldsymbol{W}_{hh}^{(f)} + \boldsymbol{b}_h^{(f)}),\\ \overleftarrow{\boldsymbol{H}}_t &= \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(b)} + \overleftarrow{\boldsymbol{H}}_{t+1} \boldsymbol{W}_{hh}^{(b)} + \boldsymbol{b}_h^{(b)}), \end{aligned} HtHt=ϕ(XtWxh(f)+Ht−1Whh(f)+bh(f)),=ϕ(XtWxh(b)+Ht+1Whh(b)+bh(b)),
其中权重 W x h ( f ) ∈ R d × h \boldsymbol{W}_{xh}^{(f)} \in \mathbb{R}^{d \times h} Wxh(f)∈Rd×h、 W h h ( f ) ∈ R h × h \boldsymbol{W}_{hh}^{(f)} \in \mathbb{R}^{h \times h} Whh(f)∈Rh×h、 W x h ( b ) ∈ R d × h \boldsymbol{W}_{xh}^{(b)} \in \mathbb{R}^{d \times h} Wxh(b)∈Rd×h、 W h h ( b ) ∈ R h × h \boldsymbol{W}_{hh}^{(b)} \in \mathbb{R}^{h \times h} Whh(b)∈Rh×h和偏差 b h ( f ) ∈ R 1 × h \boldsymbol{b}_h^{(f)} \in \mathbb{R}^{1 \times h} bh(f)∈R1×h、 b h ( b ) ∈ R 1 × h \boldsymbol{b}_h^{(b)} \in \mathbb{R}^{1 \times h} bh(b)∈R1×h均为模型参数。
然后我们连结两个方向的隐藏状态 H → t \overrightarrow{\boldsymbol{H}}_t Ht和 H ← t \overleftarrow{\boldsymbol{H}}_t Ht来得到隐藏状态 H t ∈ R n × 2 h \boldsymbol{H}_t \in \mathbb{R}^{n \times 2h} Ht∈Rn×2h,并将其输入到输出层。输出层计算输出 O t ∈ R n × q \boldsymbol{O}_t \in \mathbb{R}^{n \times q} Ot∈Rn×q(输出个数为 q q q):
O t = H t W h q + b q , \boldsymbol{O}_t = \boldsymbol{H}_t \boldsymbol{W}_{hq} + \boldsymbol{b}_q, Ot=HtWhq+bq,
其中权重 W h q ∈ R 2 h × q \boldsymbol{W}_{hq} \in \mathbb{R}^{2h \times q} Whq∈R2h×q和偏差 b q ∈ R 1 × q \boldsymbol{b}_q \in \mathbb{R}^{1 \times q} bq∈R1×q为输出层的模型参数。不同方向上的隐藏单元个数也可以不同。
总结
- 在深度循环神经网络中,隐藏状态的信息不断传递至当前层的下一时间步和当前时间步的下一层。
- 双向循环神经网络在每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列(包括当前时间步的输入)。
如果文章内容对你有帮助,感谢点赞+关注!
关注下方GZH:阿旭算法与机器学习,可获取更多干货内容~欢迎共同学习交流