tips
1. 表达式求值的时候,首先当然是从左往右看,确定优先级(只针对相邻操作符才有意义),相邻操作符按照优先级高低计算,如果(相邻)操作符的优先级相同(也就是两个操作符一毛一样了),这时候结合性才起作用。N/A表示没有结合性,L-R表示从左向右结合,R-L表示从右向左结合。接下来就是是否控制求值顺序,一般的操作符都是否,但是也有个别操作符能够控制求值的顺序,比如说逻辑与,一旦左边发现有假,右边就不会执行下去;逻辑或,一旦发现左边有真,右边也不会执行下去。包括还有条件操作符,一样道理。
2.

3. 优先级比较:( ) > [ ] > -> > ++ > -- > . > *
4. sizeof是一个操作符,不是一个函数,它算的是变量所占内存字节的大小,它后面括号里面的运算不影响数据变化(因为是在编译阶段完成的),它的返回类型是size_t,其实也就是unsigned int.
5. ++与--是有副作用的
6. 字符在代码里面其实就是一个ASCII码,因为编译器就是这么认为的。
7. 逗号表达式中的每一个表达是都会执行。因此会产生各自的效果,但是这个表达式的结果是最后一个表达式的结果。
8. 说起这个进制转换,我发现我还是要搞错。
1. 如果你想要得到一个十进制整数的n进制表达形式最后一位,就把该十进制数%n即可,如果你想要得到丢去最后一位的表达形式,就把这个十进制数/n
2. 如果你想要得到一个十进制整数的n进制的每一位,就把这个十进制数%n,然后在/n去不断更新,并以此循环,当/n后发现为0时结束。
3. 但是这种操作方法在求十进制整数的2进制表达形式时,如果碰到负数的话就会出问题,因此那个数的类型要改为unsigned int 这样的话,计算机里面存储的二进制补码仍然保持不变,但是对二进制的解读发生了变化,最高位不是符号位了。
自除数判断
题目链接:https://leetcode.cn/problems/self-dividing-numbers/
题目:

代码:
int* selfDividingNumbers(int left, int right, int* returnSize)
{
static int arr[10000]={0};
int i=0;
int count=0;
for (i=left;i<=right;i++)
{
int flag=0;
int tmp=i;
while(tmp)
{
int num=tmp%10;//最后一位
tmp/=10;//更新
if ((num==0)||(i%num!=0))
{
flag=1;
continue;
}
}
if (flag==0)
{
arr[count++]=i;
}
}
*returnSize=count;
return arr;
}经验总结:
1. 如果想要找到一个数n进制形式的每一位,就先把这个数%n,然后再/n更新,如此循环。
2. 如果想要得到一个数n进制形式下的最后一位,就把这个数%n,如果想要得到一个数除去最后一位的"那个数字形式",就把那个数/n。
3. static修饰变量,数组的意义就在把原先放在内存栈区的东西现在如果给它修饰了一下,那么它就放在静态区里面了。内存栈区里面的东西一旦进入作用域创建,出了作用域就会销毁,而静态区里面的东西都是全局的,直到程序结束之后才会被销毁。
4. 空指针的形成原因:没有初始化,越界访问,指针指向的空间被释放还给操作系统了,像上面这道题话,如果没有在数组前面用static修饰,那么这个数组是创建在栈区上,当这个函数调用结束的时候,原先的数组内存空间就会被释放,这时候你返回的那个指针就是空指针了。
除自身以外数组的乘积
题目链接:https://leetcode.cn/problems/product-of-array-except-self/
题目:

代码1:
int* productExceptSelf(int* nums, int numsSize, int* returnSize)
{
static int answer[100000];
int left[numsSize];
left[0]=1;
int right[numsSize];
right[numsSize-1]=1;
int i=0;
for (i=1;i<numsSize;i++)
{
left[i]=left[i-1]*(*(nums+i-1));
}
for (i=numsSize-2;i>=0;i--)
{
right[i]=right[i+1]*(*(nums+i+1));
}
for (i=0;i<numsSize;i++)
{
answer[i]=left[i]*right[i];
}
*returnSize=numsSize;
return answer;
}经验总结:
1. 以此为界,左右分开,寻找联系这也是一种技巧。
2. 这道题要计算除该元素以外其他元素的乘积,我们就可以以该元素为界,把数组分成左右两部分。那么该数左边的乘积乘上右边的乘积就OK了。
3. 这时候在创建两个新的数组,一个数组用来放该数左边的乘积,另一个数组用来放该数右边的乘积。最后在每个元素相乘乘起来就OK了
4. 然后就是很关键的一点,当你在算乘积的时候,别总是只会去一次又一次遍历,当多次连续计算乘积的时候,只需要在原来基础上乘1个数就完事了
代码2:
int* productExceptSelf(int* nums, int numsSize, int* returnSize)
{
static int answer[100000];
answer[0]=1;
int i=0;
for (i=1;i<numsSize;i++)
{
answer[i]=answer[i-1]*(*(nums+i-1));
}
int R=1;
for (i=numsSize-1;i>=0;i--)
{
answer[i]=answer[i]*R;
R*=(*(nums+i));
}
*returnSize=numsSize;
return answer;
}//或者这样
int* productExceptSelf(int* nums, int numsSize, int* returnSize)
{
static int answer[100000];
answer[0]=1;
int i=0;
for (i=1;i<numsSize;i++)
{
answer[i]=answer[i-1]*(*(nums+i-1));
}
int R=1;
for (i=numsSize-2;i>=0;i--)
{
R*=(*(nums+i+1));
answer[i]*=R;
}
*returnSize=numsSize;
return answer;
}经验总结:
1. 尽管上面的方法已经能够很好的去解决问题,但是还是可以进行简化。
2. 上面的方法是创建两个数组,分别用来放左侧元素的乘积与右侧元素的乘积。但是事实上,没有必要创建两个数组。可以直接把第二个数组当成输出数组。

3. 当其中一个数组计算完成之后,接下来可以一个元素一个元素边动态构造数组,边相当于把该数组渐渐变成输出结果数组。
[ ]操作符
[ ]是一个操作符哦,我们经常在数组里面碰到过它,那么它是来干什么的呢?它的本质核心事实上是这样。
1. 这个操作符有两个操作数a,b 这两个操作数位置交换一下没有任何关系,OK的。
2. 注意:
a [ b ] = b [ a ] = * (a+b)

3. 这个操作符的结合性是从右往左,因此:
a [ b ] [ c ] = * ( a [ b ] + c ) = * ( * ( a + b ) + c )
具体题目1:

答案:D
解析:

具体题目2:

答案:B.C
解析: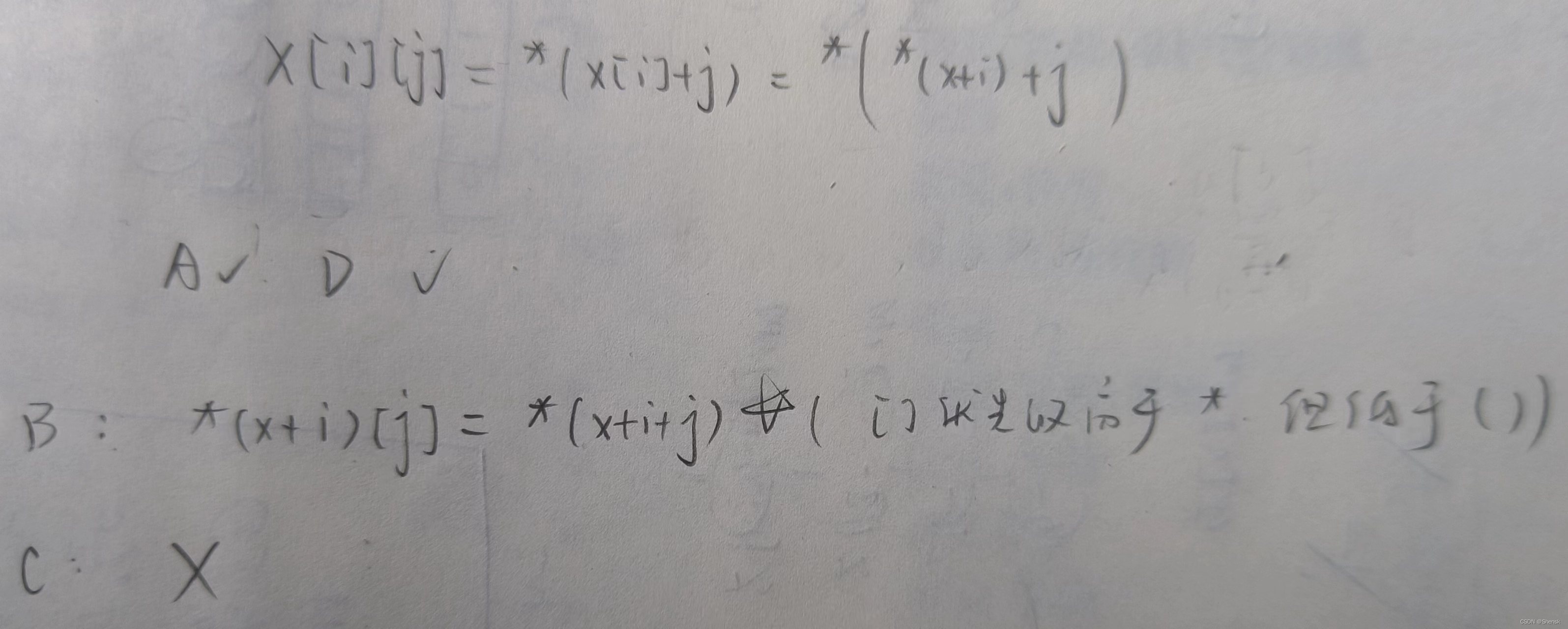
二维数组内存存储的计算
题目:

解析:

经验总结:
1. 一个字节、一个内存单元对应一个地址编号,00665544与00665548中间共有四个内存单元,也就是说四个字节。

2. 二维数组在内存当中其实也是线性存储的,这时候就用i来标记“行数”,j来标记“列数”。
3. 涉及到二维数组,有时候把它看成矩阵比较方便(但事实上根本就不是这样子存储数据的),有时候把它看成内存里面这么线性存储比较方便。
4. 每两个数减一下,算中间隔着几个数这个要会弄(有点弱智)


![C语言论坛系统[2023-01-03]](https://img-blog.csdnimg.cn/img_convert/864c3ce35adc5fd5d731cc1efe07635c.png)