用于查询性能预测的计划结构深度神经网络模型--大数据计算基础大作业

用于查询性能预测的计划结构深度神经网络模型论文阅读和复现

24.【X=1.1】在关系数据库查询优化领域，对查询时间的估计准确性直接决定了查询优化结果，进而影响到数据库整体的查询效率。但由于数据库自身的复杂性，查询时间受到数据分布、数据库负载、索引结构、数据库配置等多方面的影响，难以进行准确预测。近年来，随着AI算法的兴起，有研究者尝试使用AI模型对查询的时间进行预测并取得了一定成果。请阅读论文Plan-Structured Deep Neural Network Models for Query Performance Prediction并：
（1）提交论文阅读报告【30%分数】
（2）复现论文实验结果（可使用开源代码）【20%分数】
（3）将论文提出的模型嵌入到PostgreSQL中，使得本论文提出的代价估计方法可以被用来指导PostgreSQL的查询优化。提交代码、报告。【50%分数】

介绍

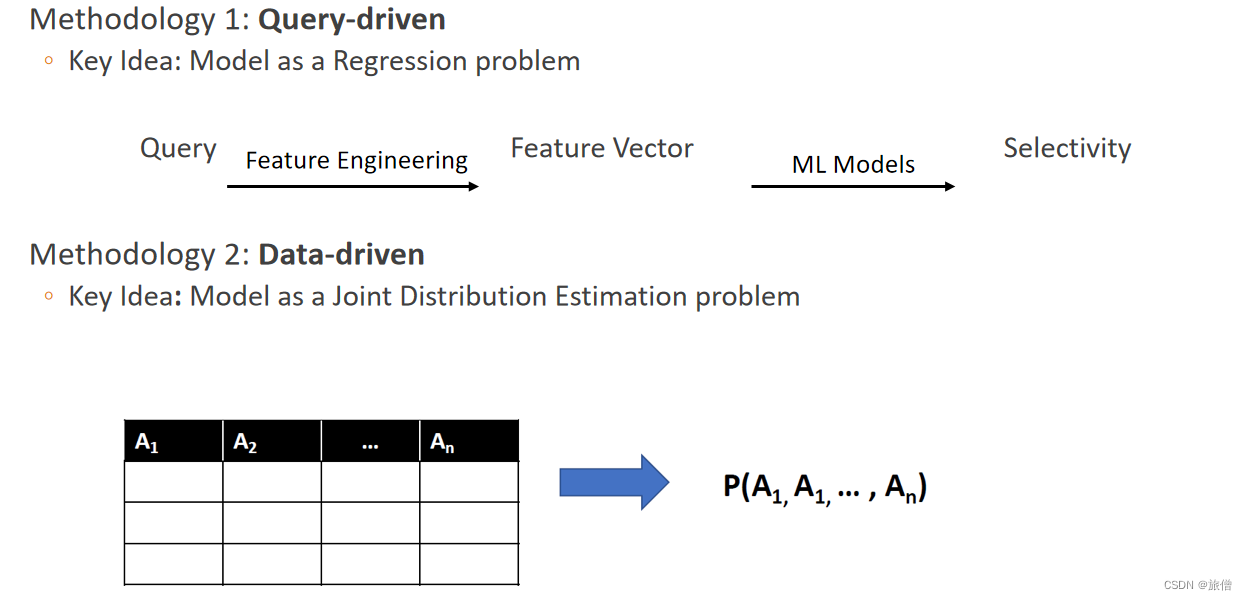
查询性能预测是预测查询延迟的任务，是数据库管理系统中最具挑战性的问题之一。现有方法依赖于人类专家设计的特征和性能模型，但通常无法捕获查询运算符和输入关系之间的复杂交互，并且通常无法自然地适应查询执行计划中的工作负载特征和模式。在本文中，我们认为深度学习可以应用于查询性能预测问题，并介绍了一种新的神经网络架构：计划结构神经网络。我们的方法消除了人工设计特征选择的需要，并在操作员和查询计划级别自动发现复杂的性能模型。我们新颖的神经网络架构可以匹配任何优化器选择的查询执行计划的结构，并高精度地预测其延迟。我们还提出了一些优化方法，可以在不牺牲有效性的情况下减少训练开销。我们在各种工作负载上评估了我们的技术，并证明我们的计划结构神经网络在查询性能预测方面可以优于最先进的技术。

实验的挑战

尽管传统的深度神经网络具有许多优点，但人们很难将其应用于查询性能预测任务中。深度学习的一个直接应用将是将整个查询建模为一个单一的神经网络，并使用查询计划特征作为输入向量。然而，这种简单的方法忽略了这样一个事实，即查询计划结构、中间结果的特征和非叶操作符通常与查询执行时间相关，因此在任何预测分析任务中都很有用。此外，查询计划是不同的结构——每个计划的操作符的类型和数量不同，操作符与查询性能有不同的相关性，操作符有不同的属性集，因此有不同的预测特征集。传统的dnn具有静态的网络架构，并处理固定大小的输入向量。
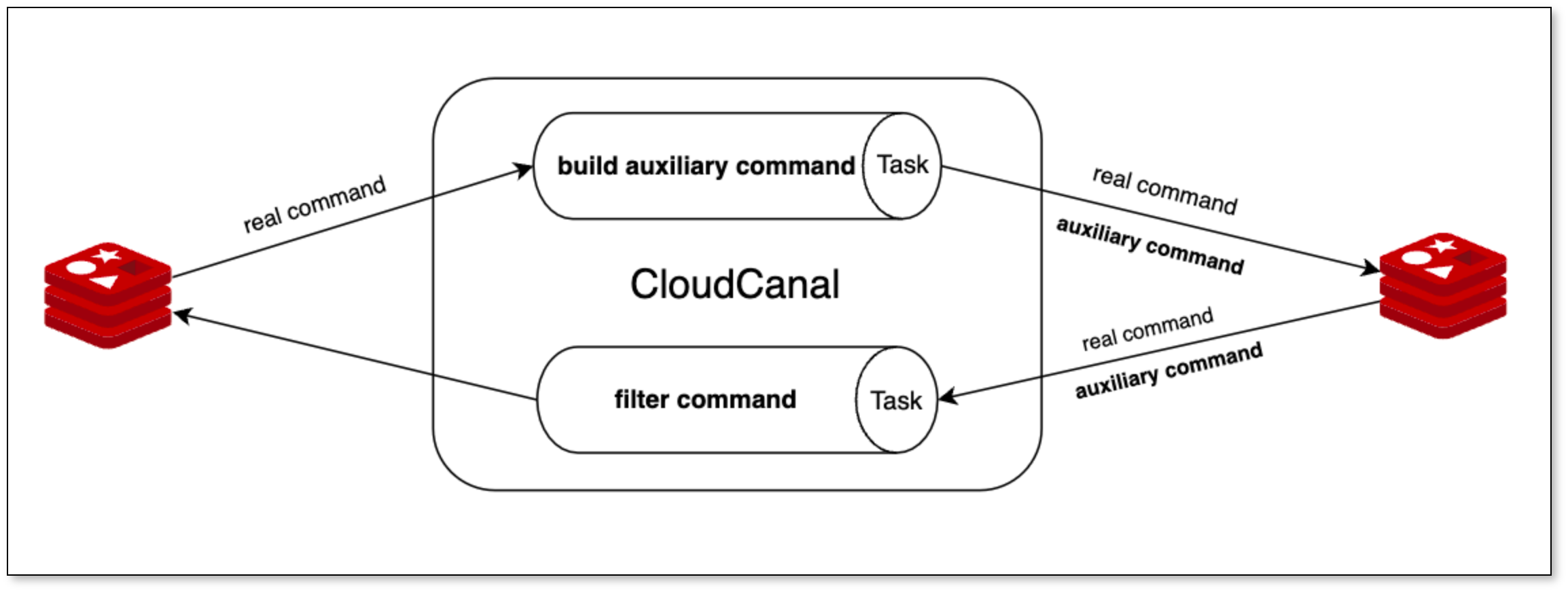
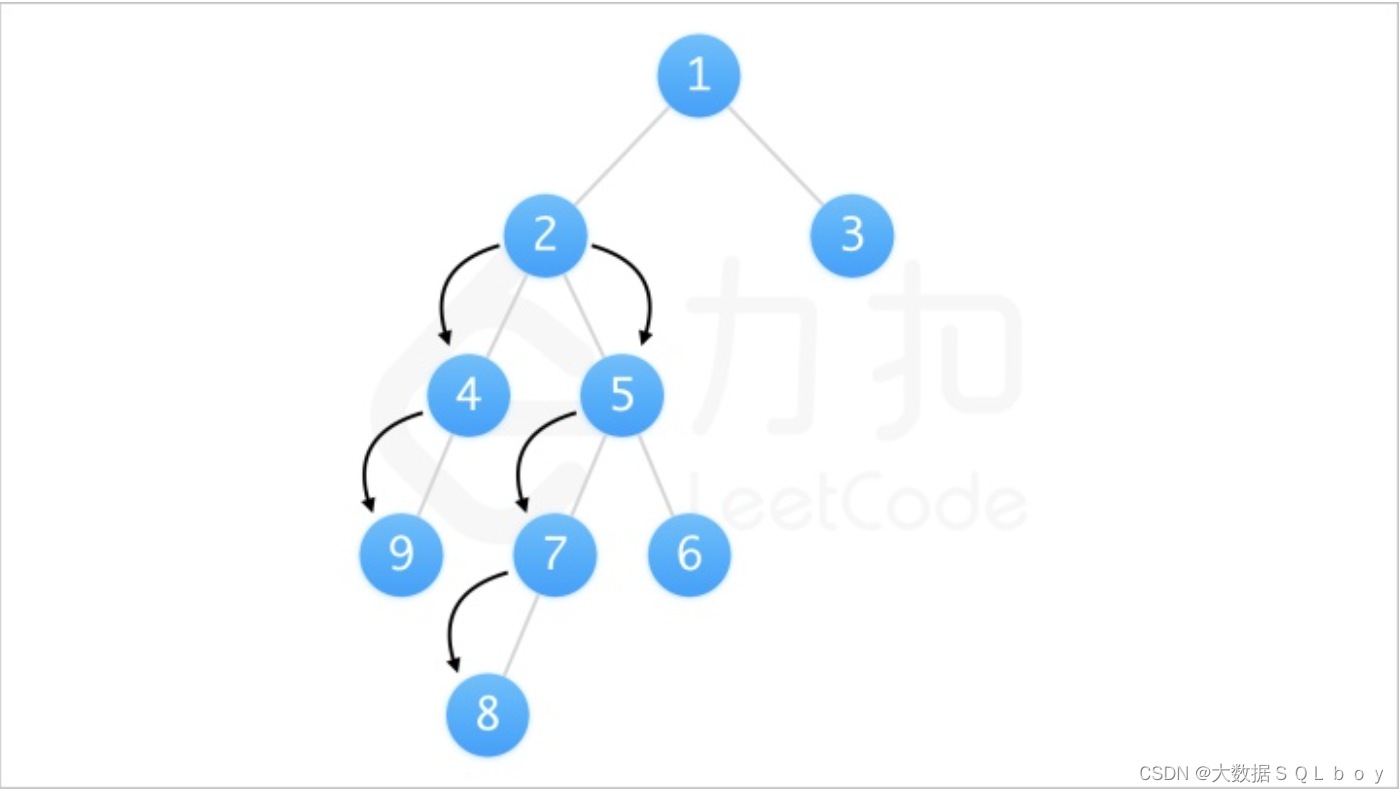
因此，“一刀切”的神经网络体系结构不适合查询性能预测任务。最后，虽然之前在机器学习领域的工作已经研究了将深度神经网络应用于序列[14]或树结构[43,49]数据，但这些方法都不适合查询性能预测，正如我们接下来描述的。用于处理树结构数据的孤立分支神经网络架构在自然语言处理[43,49]中很流行，它是基于对树的一个分支的修改会对其他分支产生巨大影响的假设，从而允许树分支共享信息。但是，在查询执行计划的上下文中，查询执行计划树的一个分支的特性和性能与其他分支合理地隔离。具体来说，我们知道一个特定的操作符只能影响它的祖先，而永远不会影响它的兄弟姐妹。例如，考虑图1中所示的两个查询执行计划。将第一个计划中的R3更改为第二个计划中的R4不会影响R1或其滤波器的性能。
异构树节点传统的神经网络处理固定结构的输入向量。但是，在查询执行计划中，每种类型的操作符都具有根本不同的属性。连接运算符可以通过连接类型（例如嵌套循环连接、哈希连接）、估计需要的存储（例如，对于外部排序）等来描述。然而，过滤器操作将具有一组完全不同的属性，例如选择性估计或并行性标志。由于不同操作符的特征向量可能有不同的大小，因此简单地将它们输入相同的神经网络是不可能的。
解决这个问题的一个简单的解决方案可能是为每个关系操作符将向量连接在一起。例如，如果一个连接运算符有9个属性，而一个过滤器运算符有7个属性，则可以用大小为9 + 7 = 16属性的向量来表示一个连接或过滤器运算符。如果运算符是一个过滤器，那么向量的前9个条目只是0，并且向量的最后7个条目将被填充。如果运算符是一个连接，则填充向量的前9个条目，最后7个条目为空。这个解决方案的问题是稀疏性：如果一个人有许多不同的操作符类型，用于表示它们的向量将有越来越大比例的零。一般来说，这种稀疏性是统计技术[22]面临的一个主要问题，将稀疏输入转换为可用的、密集的输入仍然是[52,53]研究的一个活跃领域。换句话说，使用稀疏向量来克服异构树节点，用一个潜在的更困难的问题来代替一个问题。位置独立的操作符行为正如前面的工作[13,25]所指出的，同一操作符的两个实例（例如，连接、选择等）将共享相似的行为

基于计划的神经网络

1. 传统的神经网络只是将输入的变量看成一个大的输入向量，没有考虑输入变量彼此的执行顺序也会对结果产生影响。
比如我输入(连接，选择，笛卡尔积) 12 3和 13 2的执行时间是不一样的。
2. 传统的神经网络输入长度是固定的，也就是说如果输入的长度小，我们虽然可以用null值替代，但是毕竟是一个变量，这个会对预测的结果产生一定的干扰，如果长度过长的话，我们将他拆成两个输入吗？显然这是不好的。

考虑到上述观察结果，本文提出了一种新的树状神经网络结构，其网络结构与给定查询计划的结构相匹配。这个计划结构的神经网络由操作员级的神经网络（称为神经单元）组成，整个查询计划被建模为一个神经单元的树。就其本身而言，每个神经单元预计(1)预测单个操作符类型的性能——例如，对应于连接的神经单元预测连接的延迟——以及(2)关于操作符的“有趣”数据可能对神经单元的父节点有用。计划级神经网络可以预测给定查询计划的执行时间。也就是说，也就是说相同类型的节点的代价是相等的
在这里插入图片描述
简要说明一下树状神经网络，允许有关联的节点相互通信，同时对不同分支的节点进行一个合理的隔离，选择树状模型，再合适不过。
这个树状神经网络是异构的树状网络，每一个节点的输入用代价表示或者其他，因为过滤操作会减少每一层的输入数量所以不能采用传统的神经网络。
可能的一种解决方法是：比如我有9个连接和7个过滤属性，我们就可以采用长度为16的一维向量表示，但是当不同的属性变多的时候，我们可能会填充更多的0，这样就会出现稀疏矩阵，如何把稀疏矩阵变成密集型矩阵是我们研究的另一个热点。

位置无关正确性证明

位置独立的操作级行为正如前面的工作所指出的，同一操作级的两个实例（如连接、选择等），即使在相同的计划中或在同一计划中多次出现，也会具有相似的性能特征。例如，在哈希连接的情况下，延迟与探测关系和搜索关系的大小密切相关，并且无论操作符在查询执行计划中的位置如何，这种相关性都成立。这表明，人们可以训练一个神经网络模型来预测哈希连接操作符的性能，并且当哈希连接操作符在计划中出现时，都可以使用相同的模型。

操作符号类型的神经元

由DBMS执行引擎支持的每个逻辑操作符类型建模
使用一个独特的神经单元，负责学习该特定操作符类型的性能

例如，一个唯一的连接单元，一个唯一的选择单元，等等。这些神经单元的目标是表示足够复杂的函数，以建模在各种上下文下的关系操作符的性能。
虽然一个简单的多项式模型的连接算子可以仅根据估计的输入基数进行预测，但是我们的神经单元将从大量的候选输入中自动识别出最相关的特征（例如，表的底层结构、关于数据分布的统计数据、选择性估计的不确定性、可用的缓冲空间等），所有这些都没有任何手工调整。

我们假设向量x是输入的向量，每一个列表示关系代数中的一个实例，这个向量将作为该特定操作符的神经单元的输入

来源：查询优化器，
信息：运算符的类型（例如，哈希连接或嵌套循环连接等），估计产生的行数、所需的I/O数等。
给定类型的关系操作符的每个实例都将具有相同大小的输入向量，例如，所有连接操作符都具有相同大小的输入向量，

查询执行计划中的每个节点都被映射到与关系操作符对应的神经单元。
在这里插入图片描述

输出向量
操作符实例x的性能信息通常与查询执行计划中它的父操作符的性能相关。为了捕获这一点，并允许操作符级神经单元之间的信息流，一个操作符类型的每个神经单元将同时输出一个延迟预测和一个数据向量。当延迟输出预测操作符的延迟时，输出数据向量表示子操作符中与父操作符的性能相关的“有趣的”特性。例如，扫描操作符的神经单元可以产生一个数据向量，其中包含关于所产生的行的预期分布的信息。我们注意到，这些数据向量是由模型在其训练阶段自动学习的，而不需要任何人为干扰或选择出现在输出向量中的特征。

神经元：这个输入通过许多隐藏层来输入，每个隐藏层通过应用一个激活的仿射变换（如公式1所定义）来生成特征。这些复杂的变换可以通过梯度下降方法自动学习，该方法逐步调整神经单元NA的权重和偏差，以最小化其损失函数（如第2.2节所述）。最后一层将隐藏层学习到的内部表示转换为延迟预测和输出数据向量。在形式上，一个神经单元NA的输出被定义为：
在这里插入图片描述
其中a是操作符类型a的实例。输出向量的大小为d + 1。输出向量的第一个元素表示神经单元对算子延迟的估计，记为p→a[l]。其余的d个元素表示数据向量，记为p→a[d].我们注意到，由于不同神经单元的输入向量不会有相同的大小，每个神经单元可能有不同大小的权重和偏差向量，但它们的基本结构将是相似的。
在这里插入图片描述

方法简要介绍

模型的优点

我们的计划结构的神经网络模型消除了上述的一些挑战，同时利用了一些计划结构的属性（见第3节）。
分支隔离由于我们知道查询执行计划中的任何特定关系操作符只能影响其祖先的性能，而不能影响它的兄弟或子节点的性能，因此我们说查询执行计划显示分支隔离。我们将神经单元组装成树的方式尊重这一特性：每个神经单元只向上传递信息。直观地说，这种只向上的通信策略直接将有关查询执行计划结构的知识编码到网络体系结构本身中。
异构树节点操作符级神经单元接受不同大小的输入向量，这取决于他们所建模的操作符，同时产生一个固定大小的输出向量。这使得具有计划结构的神经网络的结构能够动态地匹配任何给定的查询计划，从而使我们的模型适合于处理任意的计划。例如，无论连接算子的子节点是过滤器（选择）还是扫描，它的子神经单元都将产生一个固定大小的向量，允许这个输出向量连接到表示连接算子的神经单元。
与位置无关的操作符行为由于我们期望一个特定的操作符具有一些共同的性能特征，而不管其在查询执行计划中的位置如何，因此对一个特定操作符的每个实例都使用相同的神经单元。因为相同的查询执行计划可以包含多个实例相同的操作符类型（例如，多个连接），我们的架构可以被认为是一个递归神经网络[26]，因此好处：因为实例相同的操作符共享相似的属性，代表他们与一个神经单元（因此一组权重和偏差）是高效和有效的。然而，由于不同的操作符类型由不同的神经单元表示（因此不会共享相同的权值和偏差），我们的方法可以处理查询执行计划操作符的异构性质。

代码的运行

本文使用了开源代码，引用链接

生成QPP processed plan

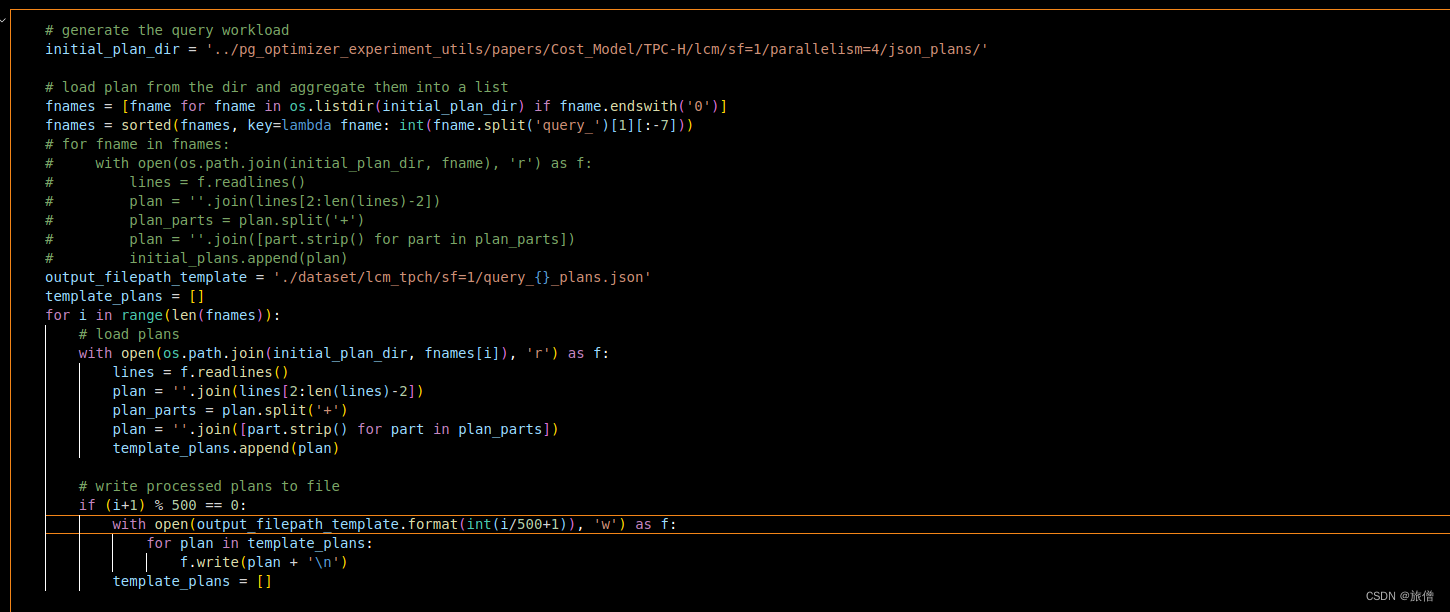
在这里插入图片描述

准备TPH数据集

在这里插入图片描述

结果

在这里插入图片描述

初始化和训练QPP网路

在这里插入图片描述

logf = open(opt.logfile, 'w+')
save_opt(opt, logf)
#qpp.test_dataset = dataset.create_test_data(opt)
qpp.test_dataset = dataset.test_dataset

total_iter = 0
for epoch in range(opt.start_epoch, opt.end_epoch):
# for epoch in range(0, opt.end_epoch):
    epoch_start_time = time.time()  # timer for entire epoch
    iter_data_time = time.time()    # timer for data loading per iteration
    epoch_iter = 0                  # the number of training iterations in current epoch, reset to 0 every epoch

    samp_dicts = dataset.sample_data()
    total_iter += opt.batch_size

    qpp.set_input(samp_dicts)
    qpp.optimize_parameters(epoch)
    logf.write("epoch: " + str(epoch) + "; iter_num: " + str(total_iter) \
                + '; total_loss: {}; test_loss: {}; pred_err: {}; R(q): {}' \
                .format(qpp.last_total_loss, qpp.last_test_loss,
                        qpp.last_pred_err, qpp.last_rq))

    #if total_iters % opt.print_freq == 0:    # print training losses and save logging information to the disk
    losses = qpp.get_current_losses()
    loss_str = "losses: "
    for op in losses:
        loss_str += str(op) + " [" + str(losses[op]) + "]; "

    if epoch % 50 == 0:
        print("epoch: " + str(epoch) + "; iter_num: " + str(total_iter) \
                + '; total_loss: {}; test_loss: {}; pred_err: {}; R(q): {}' \
                .format(qpp.last_total_loss, qpp.last_test_loss,
                        qpp.last_pred_err, qpp.last_rq))
        print(loss_str)


    logf.write(loss_str + '\n')

    if (epoch + 1) % opt.save_latest_epoch_freq == 0:   # cache our latest model every <save_latest_freq> iterations
        print('saving the latest model (epoch %d, total_iters %d)' % (epoch + 1, total_iter))
        qpp.save_units(epoch + 1)

logf.close()

实验结果

在这里插入图片描述

模型的存放

环境：Linux虚拟机
vscode python3环境，左边是模型的存放位置，我们训练不同数据量以及不同的操作，为了使实验结果更准确，我们采用大量的数据进行模拟，为此光训练部分已经跑了两天。
在这里插入图片描述

将代码嵌入到模拟的psql中

在这里插入图片描述

获取查询计划中的信息(小样本生成以及实验)

我们的主要想法是写一个小型数据库系统并模拟查询之后我们为这个数据库建立一个接口，使用onnx模型和本实验训练得到的模型进行嵌入，观察实验的效果，指导查询执行。

在这里插入图片描述
输入特征向量我们用向量x表示x = F(x),这个向量将作为该特定操作符的神经单元的输入。这些向量可以从查询优化器的输出中提取，并包含以下信息：操作符的类型（例如，哈希连接或连接操作符的嵌套循环连接等），估计要产生的行数、所需的估计I/Os数等。
在这里插入图片描述

查询生命周期的过程

第一阶段是通过JDBC/ODBC（分别由Microsoft和Oracle创建的用于与数据库交互的API）或通过其他方式如PSQL（Postgres的终端前端）连接到数据库。
第二阶段是将查询转换为称为解析树的中间格式。讨论解析树的内部结构超出了本文的范围，但您可以想象它就像SQL查询的编译形式。
第三阶段就是我们所说的重写系统/规则系统。它采用从第二阶段生成的解析树，并以计划器/优化器可以开始在其中工作的方式重写它。
第四阶段是最重要的阶段，也是数据库的核心。如果没有计划器，执行器就会对如何执行查询、使用什么索引、是否扫描较小的表以消除更多不必要的行等问题一无所知。这个阶段就是我们将在本文中讨论的。
第五个也是最后一个阶段是执行器，它执行实际执行并返回结果。几乎所有的数据库系统都遵循一个或多或少与上述类似的过程。

计划和时间分析

对psql进行一个简单的查询

EXPLAIN SELECT * FROM fake_data LIMIT 10;

在这里插入图片描述
解释分析

在这里插入图片描述

将ANALYZE参数添加到查询会产生计时信息。
与EXPLAIN不同，EXPLAIN ANALYSE实际上在数据库中运行查询。这个选项对于了解计划器是否没有正确发挥其作用非常有帮助，即，从EXPLAIN和EXPLAIN ANALYSE生成的计划是否存在巨大差异。

缓冲区

Buffers:sharedhit=5意味着从PostgreSQL缓存本身获取了五个页面。让我们调整查询以从不同的行偏移。
在这里插入图片描述
更改OFFSET会导致不同的页面点击次数。

Buffers:sharedhit=7read=5显示5页来自磁盘。该read部分是显示有多少页面来自磁盘的变量，正如已经解释过的hit来自缓存。如果我们再次执行相同的查询（记住ANALYSE运行查询），那么所有数据现在都来自缓存。

在这里插入图片描述

再次执行查询意味着缓存现在提供所有结果。PostgreSQL使用一种称为LRU（最近最少使用）缓存的机制将经常使用的数据存储在内存中。

查询计划信息格式化输出

PostgreSQL能够以一种很好的格式给出查询计划，例如JSON，这些计划可以以一种语言中立的方式进行解释

EXPLAIN (ANALYSE,BUFFERS,VERBOSE,FORMAT JSON) SELECT * FROM fake_data LIMIT 10 OFFSET 500;

将按JSON格式打印查询计划。您可以通过复制其输出并将其插入到另一个表中来在Arctype中查看此格式，如下面的图片所示。
在这里插入图片描述

小样本的任务和结果

根据SQL查询语句，预测查询规模

SQL类型

数值型数据（范围查询与等值查询）
最多涉及两表连接
提供查询计划

最后我们的目的是提供10000条训练集，需要预测2000条测试集的结果

数据解释

在这里插入图片描述

结果

中间结果存放在 ipynb的内容中等，老师可以阅读和运行代码。
在这里插入图片描述

在这里插入图片描述

嵌入到大型数据库

通过刚才小型实验的机器学习算法预测查询计划，我们取得了比较不错的效果，现在我们将训练好的模型嵌入psql开源代码中。

将pytorch文件转换成onnx文件

代码switch.py

import os
import torch
from functools import partial
from model_arch import NeuralUnit  # 替换成你的模型类所在的模块

num_rel = 8
max_num_attr = 16
num_index = 22
SCALE = 1
num_per_q = 500

TRAIN_TEST_SPLIT = 0.8

tpch_dim_dict = {'Seq Scan': num_rel + max_num_attr * 3 + 3 ,
                 'Index Scan': num_index + num_rel + max_num_attr * 3 + 3 + 1,
                 'Index Only Scan': num_index + num_rel + max_num_attr * 3 + 3 + 1,
                 'Bitmap Heap Scan': num_rel + max_num_attr * 3 + 3 + 32,
                 'Bitmap Index Scan': num_index + 3,
                 'Sort': 128 + 5 + 32,
                 'Hash': 4 + 32,
                 'Hash Join': 11 + 32 * 2, 'Merge Join': 11 + 32 * 2,
                 'Aggregate': 7 + 32, 'Nested Loop': 32 * 2 + 3, 'Limit': 32 + 3,
                 'Subquery Scan': 32 + 3,
                 'Materialize': 32 + 3, 'Gather Merge': 32 + 3, 'Gather': 32 + 3}
                 

def convert_to_onnx(model_path, output_path, model_factory, input_size: tuple):
    # 加载模型的状态字典
    state_dict = torch.load(model_path, map_location=torch.device('cpu'))

    # 创建模型对象 也就是神经网络模型 QPP是包装而不是神经网络
    model = model_factory()  # 请替换成你的模型类
    model.load_state_dict(state_dict)
    model.eval()

    # 创建虚拟输入数据
    dummy_input = torch.randn(*input_size)

    # 导出模型到ONNX格式
    torch.onnx.export(model, dummy_input, output_path, verbose=True)


def convert_net(prefix: str, net_type: str, modeldir: str, outdir: str) -> None:
    model_path = os.path.join(modeldir, f"{prefix}_net_{net_type}.pth")
    out_path = os.path.join(outdir, f"{prefix}_net_{net_type}.onnx")
    convert_to_onnx(model_path, out_path, partial(NeuralUnit, net_type, tpch_dim_dict), (32, tpch_dim_dict[net_type]))


if __name__ == "__main__":
    folder_path = "saved_model"  # 替换成你的文件夹路径
    output_folder = "onnx_models"  # 输出ONNX文件的文件夹

    # 确保输出文件夹存在
    os.makedirs(output_folder, exist_ok=True)

    for ops in tpch_dim_dict:
        convert_net("best", ops, folder_path, output_folder)

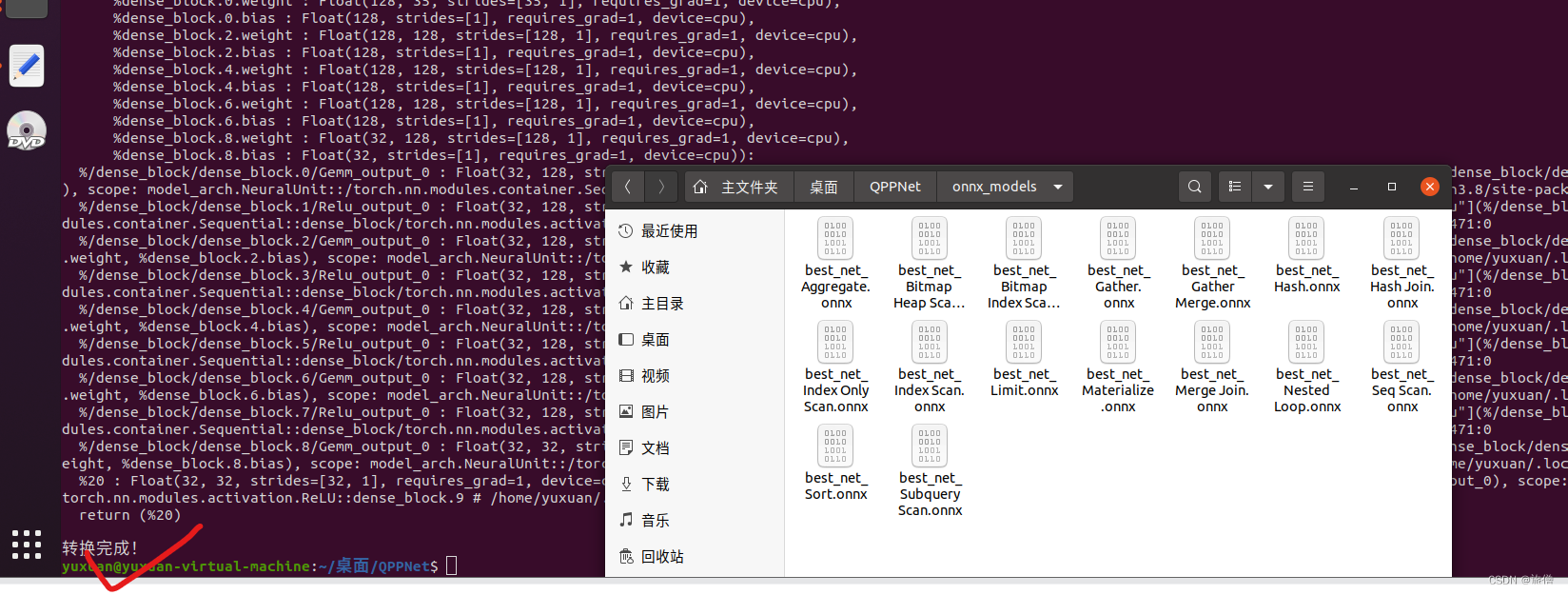
    print("转换完成！")